Suites
numériques, bac S 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
......
.....
|
Amérique du nord.
Partie A : établir
une inégalité
Sur l’intervalle [0;+∞[ , on définit la fonction 𝑓 par
𝑓(𝑥)=𝑥−ln(𝑥+1).
1. Étudier le sens
de variation de la fonction 𝑓 sur l’intervalle [0;+∞[.
f '(x) = 1-1/(x+1) = x /(x+1), positive sur [0;+∞[.
f(x) est strictement croissante sur [0;+∞[.
2. En déduire que
pour tout 𝑥∈[0;+∞[, ln (𝑥+1)≤𝑥.
f(0) = 0 -ln(1) = 0.
De plus f(x) est strictement croissante.
par suite f(x) > 0
; ln (𝑥+1)≤𝑥.
Partie B :
application à l’étude d’une suite
On pose 𝑢 0=1 et pour tout entier naturel 𝑛, 𝑢 𝑛+1=𝑢 𝑛−ln
(1+𝑢 𝑛). On admet que la suite de terme général 𝑢 𝑛
est bien définie.
1. Calculer une
valeur approchée à 10 −3 près de 𝑢 2.
u 1 = u 0 -ln(1+u 0) = 1 - ln2 ~ 0,307
u 2 = u 1 -ln(1+u 1) ~ 0,307 -ln1,307 ~ 0,039.
2. a. Démontrer par
récurrence que pour tout entier naturel 𝑛, 𝑢 𝑛≥0.
Initialisation
: la propriété est vraie au rang zéro.
Hérédité :
la propriété est suposée vraie au rang p : 𝑢 p ≥0.
u p+1 =u p - ln(1+u p) ; or ln(1+u p)
< u p
; donc u p+1 >
0.
Conclusion :
la propriété est vraie au rang zéro et héréditaire, elle est donc vraie
quel que soit n.
b. Démontrer que
la suite (𝑢 𝑛) est décroissante, et en déduire que pour
tout entier naturel 𝑛, 𝑢 𝑛≤ 1 .
u n+1-u n = - ln(1+u n) avec n(1+u n)
>0 ;
donc u n+1 < u n.
La suite est décroissante.
c. Montrer que la
suite (𝑢𝑛) est convergente.
La suite est décroissante et minorée par 0, donc elle converge.
3. On note 𝑙 la
limite de la suite (𝑢 𝑛) et on admet que 𝑙=𝑓(𝑙) où 𝑓
est la fonction définie dans la partie A. En déduire la valeur de 𝑙.
l = l-ln(1+ l) ; ln(1+ l) = 0 = ln(1) ; l = 0.
4. a. Écrire un
algorithme qui, pour un entier naturel 𝑝 donné, permet de déterminer
le plus petit rang N à partir duquel tous les termes de la suite (𝑢 𝑛)
sont inférieurs à 10 −𝑝.
à U on affecte 1
à N on affecte 0
Tant que U > 10-p
à U on affecte U-ln(1+U)
N = N+1
Fin tant que.
b. Déterminer le
plus petit entier naturel 𝑛 à partir duquel tous les termes de la
suite (𝑢𝑛) sont inférieurs à 10 −15 .
u 0 = 1 ; u 1 = 1 -ln(2) = 0,307 ; u 2 =
0,307 -ln(1,307) = 3,9 10 -2 ; u 3 = 3,9 10 -2
-ln(1,039) = 7,4 10 -4 ;
u 4 = 7,4 10 -4 -ln(1+7,4 10 -4) = 1,013
10 -6 ; u 5 = 1,013 10 -6 -ln(1+1.013 10 -6)
= 5,131 10 -13 ;
u 6 = 5,131 10 -13 -ln(1+5,131 10 -13) =
1,58 10 -17 ;
n = 6.
Centres étrangers
Le but de cet exercice est d’étudier la suite (un) définie par la donnée de son premier terme u1 et, pour tout entier naturel n supérieur ou égal à 1, par la relation :
un+1 = (n+1) un-1.
Partie A.
1. Vérifier, en détaillant le calcul, que si u1 = 0 alors u4 = −17
u2 = (1+1) u1-1=-1 ;
u3 = (2+1) u2-1=-4 ;
u4 = (3+1) u3-1=-17.
2. Recopier et compléter l’algorithme ci-dessous pour qu’en saisissant préalablement dans U une valeur de u1 , il calcule les termes de la suite (un ) de u2 à u13
U = "valeur de u1".
Pour N allant de 1 à 12
U = (N+1) *U-1
Fin Pour
3. On a exécuté cet algorithme pour u1 = 0,7 puis pour u1 = 0,8 . Voici les valeurs obtenues.
Pour u1 = 0,7
|
0,4
|
0,2
|
-0,2
|
-2
|
-13
|
-92
|
-737
|
-6634
|
-729752
|
-8757025
|
Pour u1 = 0,8
|
0,6
|
0,8
|
2,2
|
10
|
59
|
412
|
3295
|
29654
|
296539
|
3261928
|
Quelle semble être la limite de cette suite si u1 = 0,7 et si u1 = 0,8 ?
Si u1 = 0,7 la suite tend vers moins l'infini et si u1 = 0,8 la suite tend vers plus l'infini.
Partie B.
On considère la suite ( In) définie pour tout entier naturel n, supérieur ou égal à 1, par :
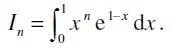
On rappelle que le nombre e est la valeur de la fonction exponentielle en 1, c’est-à-dire que e = e1 .
1. Prouver que la fonction F définie sur l’intervalle [0;1] par F(x) =(-1-x)e1-x est une primitive sur l’intervalle [0;1] de la fonction f définie sur l’intervalle [0;1] par f(x) = xe1-x.
Dériver F(x) en posant u = -1-x et v = e1-x ; u' = -1 ; v' = -e1-x ;
u'v + v'u = -e1-x +(1+x)e1-x = xe1-x = f(x).
2. En déduire que I1 = e − 2 .
I1 = F(1) -F(0) = (-1-1)e1-1 - (-1-0)e1-0 = -2+e.
3. On admet que, pour tout entier naturel n supérieur ou égal à 1, on a :
In+1 = (n+1)In-1.
Utiliser cette formule pour calculer I2 .
I2 = (1+1)I1-1 = 2(e-2)-1=2e-5.
4. a)
Justifier que, pour tout nombre réel x de l’intervalle [0;1] et pour
tout entier naturel n supérieur ou égal à 1, on a : 0 < xne1-x < xne.
0 < x <1 ; 0 > -x > -1 ; 0+1 > -x+1 > -1 +1 ; 1 > -x+1 > 0 ou encore 0 < -x+1 < 1.
La fonction exponentielle étant strictement croissante sur R :
e0 =1 < e1-x < e1.
Multiplier par xn strictement positif :
xn < xne1-x < xne1.
cette inégalité est aussi vérifiée pour x = 0.
b) Justifier que :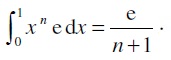
Une primitive de xn est xn+1 / (n+1) ;
pour n > 1, une primitive de e xn est e xn+1 / (n+1) ;
par suite sur l'intervalle [0 ; 1 ] : e 1n+1 / (n+1)- e 0n+1 / (n+1) = e / n+1).
.
c) En déduire que, pour tout entier naturel n supérieur ou égal à 1, on a : 0 < In < e /(n+1).
D'après la question B.4.a : 0 < xne1-x < xne.
Intégrer sur [0 ; 1] cette inégalité : 0 < In < e /(n+1)..
d) Déterminer la limite de In en plus l'infini.
D'après le théorème d'encadrement In tend vers zéro si n tend vers plus l'infini.
Partie C.
Dans cette partie, on note n! le nombre défini, pour tout entier naturel n supérieur ou égal à 1, par :
1!=1
2!= 2×1
et si n > 3 :
n!= n x (n −1)×....×1
On a ainsi par exemple
3!= 3×2×1= 3×(2×1) = 3×2!
4!= 4×3×2×1= 4×(3×2×1) = 4×3!
8!= 8×7×6×5×4×3×2×1= 8×(7×6×5×4×3×2×1) = 8×7!
Et, plus généralement :
(n +1)! = (n +1)× n!
1. Démontrer par récurrence que, pour tout entier naturel n supérieur ou égal à 1, on a : un =n!(u1-e+2)+In.
On rappelle que, pour tout entier naturel n supérieur ou égal à 1, on a :
un+1 = (n+1) un -1 et In+1 =(n+1)In-1.
Inittialisation : I2 = 2e-5 ; u2 = 2u1-1 ; u2-I2 =2u1-1-2e+5 =2u1+4-2e = 2(u1+2-e) =2!(u1+2-e).
u2 =2!(u1+2-e)+I2. La relation est vraie au rang 2.
Hérédité : la relation est supposée vraie au rang p : up =p!(u1-e+2)+Ip.
(p+1)up =(p+1)p!(u1-e+2)+(p+1)Ip.
(p+1)up -1=(p+1)p!(u1-e+2)+(p+1)Ip-1.
Or (p+1)p! = (p+1)!.
up+1=(p+1)! (u1-e+2)+Ip+1-1.
La relation est vraie au rang p+1.
Conclusion : la relation est vraie au rang 2 et héréditaire, elle est vraie pour tout entier n supérieur ou égal à 1.
2. On admet que la limite en plus l'infini de n! est égale à plus l'infini.
a) Déterminer la limite de la suite (un ) lorsque u1 = 0,7 .
un =n!(0,7-e+2)+In = n!(2,7-e)+In.
In tend vers zéro si n tend vers plus l'infini ; la limite en plus l'infini de n! est égale à plus l'infini.
De plus 2,7-e est négatif.
Si u1 = 0,7 la suite tend vers moins l'infini
b) Déterminer la limite de la suite ( un) lorsque u1 = 0,8 .
un =n!(0,8-e+2)+In = n!(2,8-e)+In.
In tend vers zéro si n tend vers plus l'infini ; la limite en plus l'infini de n! est égale à plus l'infini.
De plus 2,8-e est positif.
Si u1 = 0,8 la suite tend vers plus l'infini
|
...
|
|
Polynésie.
On considère la suite (In) définie par 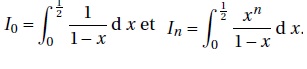
1. Montrer que I0 = ln(2).
Une primitive de 1 / (1-x) est -ln(1-x) ; I0 =- [ln(1-0,5) -ln(1)] = -ln(0,5) = ln(2).
2. a. Calculer I0 −I1.
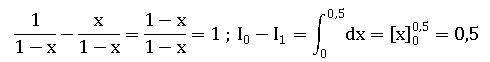
b. En déduire I1.
I1 =ln(2)- 0,5.
3. a. Montrer que, pour tout entier naturel n, In −In+1 =0,5n+1 / (n+1).
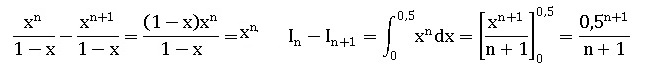 . .
b. Proposer un algorithme permettant de déterminer, pour un entier naturel n donné, la valeur de In.
Variables
I, réel ; a, n entier
I = ln(2)
Pour a allant de 1 à n
I =I- 0,5a / a
Fin pour.
4. Soit n un entier naturel non nul.
On admet que si x appartient à l’intervalle [0 ; 0,5] alors 0 < xn / (1-x) < 1 / 2n-1.
a. Montrer que pour tout entier naturel n non nul, 0 < In < 1 / 2n.
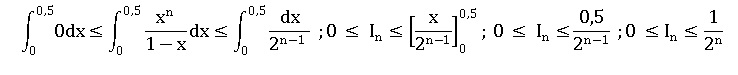
b. En déduire la limite de la suite (In) lorsque n tend vers +∞.
1 / 2n tend vers zéro si n tend vers plus l'infini.
D'après le théorème d'encadrement, In tend vers zéro si n tend vers plus l'infini.
5. Pour tout entier naturel n non nul, on pose
Sn =0,5 +0,52 /2 +0,53 / 3 +.... +0,5n / n.
a. Montrer que pour tout entier naturel n non nul, Sn = I0 - In.
Sn = 0,5 +0,52 /2 +0,53 / 3 +.... +0,5n / n.
I0 −I1 =0,5 ; I1 −I2 =0,52 / 3 ; I2 −I3 =0,53 / 4 ; In-1 −In =0,5n / n.
Sn =I0 −I1 + I1 −I2 +I2 −I3 +..... + In-1 −In =I0 - In.
b. Déterminer la limite de Sn lorsque n tend vers +oo.
In tend vers zéro si n tend vers plus l'infini.
Sn tend vers I0 = ln(2) si n tend vers plus l'infini.
|
....
|
Amérique du sud.
On considère la suite (un) définie pour tout entier n >0 par : un+1 = 3-10 / (un+4) et
u0 = 5.
Partie A :
1. Déterminer la valeur exacte de u1 et de u2.
u1 = 3-10 / (u0+4) = 3-10 / 9 =(27-10) / 9 = 17 / 9.
u2 = 3-10 / (u1+4) = 3-10 / (17 / 9 +4) =3-90 / 53 =(159-90) / 53 = 69 / 53.
2. Démontrer par récurrence que pour tout entier naturel n, un >1.
Initialisation : u1 =17 / 9.La relation est vraie au rang 1.
Hérédité : On suppose que up >1 est vraie
up+1 = 3-10 / (up+4) avec up+4 > 5.
1 / (up+4) < 1 / 5 ; 10 / (up+4) < 10 / 5 ; 10 / (up+4) < 2 ;
-10 / (up+4) > -2 ;
3-10 / (up+4) > 3-2 ; 3-10 / (up+4) > 1 ; up+1 >1, la propriété est vraie au rang p+1.
Conclusion : la propriété étant vraie au rang 1 et héréditaire, elle est vraie pout tout entier naturel.
3. Démontrer que, pour tout entier nature n, un+1 −un =(1−un ) (un +2) / ( un +4).
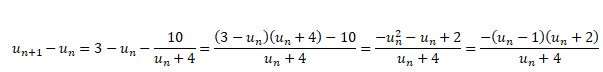
4. En déduire le sens de variation de la suite (un).
un > 1 ; (un +2) et ( un +4) sont positifs ; (1−un ) est négatif ou nul.
un+1 −un < 0. La suite est décroissante.
5. Justifier que la suite (un) converge.
La suite est décroissante et minorée ( un > 1), donc elle converge.
Partie B :
On considère la suite (vn) définie pour tout entier naturel n par vn =(un-1) / (un+2).
1. a. Démontrer que (vn) est une suite géométrique dont on déterminera la raison et le premier terme v0.
vn+1 =(un+1-1) / (un+1+2).
un+1 = 3-10 / (un+4).
un+1-1 = 2-10 / (un+4) =(2un-2) / (un+4).
un+1+2=5-10 / (un+4) =(5un+10) / (un+4).
vn+1 =(2un-2) / (5un+10) =2 / 5 vn.
(vn) est une suite géométrique de raison 2 /5 = 0,4 et de premier terme v0 = (u0-1) / (u0+2)=4 / 7.
b. Exprimer vn en fonction de n.
En déduire que pour tout entier naturel n, vn diffère de 1.
vn =v0 x 0,4n=4 / 7x 0,4n.
4 / 7 diffère de 1 ; 0,4n est inférieur ou égal à 1 ; donc vn diffère de 1.
2. Démontrer que pour tout entier naturel n, un =(2vn +1) / (1−vn).
vn =(un-1) / (un+2)=4 / 7x 0,4n.
vn(un+2)=un-1 ; vn un+2vn=un-1 ; un ( 1-vn) = 1+2vn ; un =(2vn +1) / (1−vn).
3. En déduire la limite de la suite (un).
un =(8 / 7x 0,4n +1) / (1−4 / 7x 0,4n).
Quand n tend vers plus l'infini : 0,4n tend vers zéro.
1−4 / 7x 0,4n tend vers 1 et 8 / 7x 0,4n +1 tend vers 1.
La limite de cette suite (un) est égale à 1.
Partie C :
On considère l’algorithme ci-dessous.
1. Après exécution de l’algorithme, quelle valeur est contenue dans la variable n ?
2. À l’aide des parties A et B, interpréter cette valeur.
u←5
n←0
Tant que u >1,01
n←n +1
u←3− 10 /(u +4)
Fin du Tant que
L'algorithme s'arrète dès que u <1,01.
u5 =(8 / 7x 0,45 +1) / (1−4 / 7x 0,45)~1,0176.
u6 =(8 / 7x 0,46 +1) / (1−4 / 7x 0,46)~1,0073.
n est égal à 6.
La suite (un) est décroissante e converge vers1.
L'algorithme affiche la première valeur de n pour laquelle un <1,01.
|
|