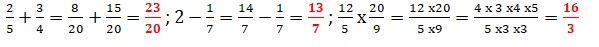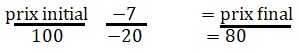Mathématiques,
première technologique ST2S, STI2D, contrôle continu.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Partie 1. 10 points.
1 à 3 Fraction irréductible égale à :
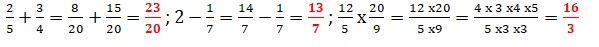
4 et 5. Compléter : 2 / 5 x.... = 3 ; 3 x5 / 2 = 7,5.
8 x fois .... = 56 x3 ; 56 x3 /(8x) = 7x2.
6. Calculer 30 % de 70.
0,30 x70 = 21.
7. Si T = 2 p / w, alors w = 2p / T.
8. Développer : -3x(1-2x) = -3x +6x2.
9. Factoriser (x+2) (x-3) -2(x+2) = (x+2)(x-3-2) = (x+2)(x-5).
10. f(x) =x2-4x. Calculer f(-2).
f(2) = (-2)2 -4*(-2) = 4 +8 = 12.
11. Une réduction de 20% d’un article représente une diminution du prix de 7 €.
Quel était le prix de cet article avant réduction ?
Prix initial -réduction = prix final.
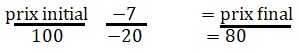
Faire les produits en croix : 20 prix initial = 100 x 7.
Prix initial = 700 / 20 = 35 €.
12. Compléter 2,7 1010 est égal à ..... milliards.
2,7 1010 = 2,7 x10 x109 = 27 milliards.
13 à 16. 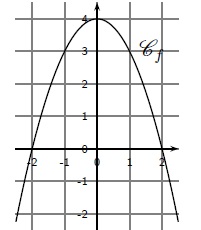
L'image de 0 par f est 4.
Un antécédent de 0 par f est 2 ou -2.
L'ensemble des solutions de f(x) = 3 est -1 et 1.
L'ensemble des solutions de f(x) >0 est ]-2 ; 2 [.
17 et 18. Donner l'équation réduite de la droite D ainsi que le tableau des signes de cette fonction affine.

y = ax +b.
b = 2 ordonnée à l'origine.
Pente de la droite - 2 /3.
y = -2 /3 x +2.
19. L'équation réduite de la droite D est y = 2,5 x-13. Compléter : A (6 ; ....) appartient à D.
y =2,5 *6 -13 =15-13 = 2.
20. Compléter :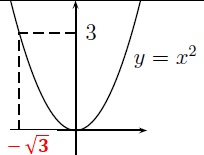
|
...
|
|
Partie 2.
Exercice 1.(5 points)
Partie A : Etude d’une fonction
Soit f la fonction définie sur R par f(x) = 0,005x(x + 56).
1. Quelle est la nature de la courbe représentative de f ?
2. Représenter l’allure de la courbe représentative de f en précisant :
— les abscisses des points d’intersection de Cf avec l’axe des abscisses ;
— l’axe de symétrie de Cf ainsi que son équation.
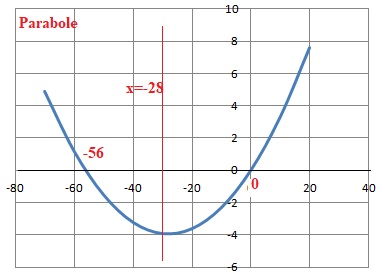
f(x) = 0,005 x2 +0,28 x ; a = 0,005 ; b = 0,28 ; -b / (2a) = -0,28 / 0,01 = -28.
On s’intéresse dans la suite de cet exercice à la distance d’arrêt en
mètres d’un véhicule sur route humide, puis sur route sèche, en
fonction de sa vitesse en km/h.
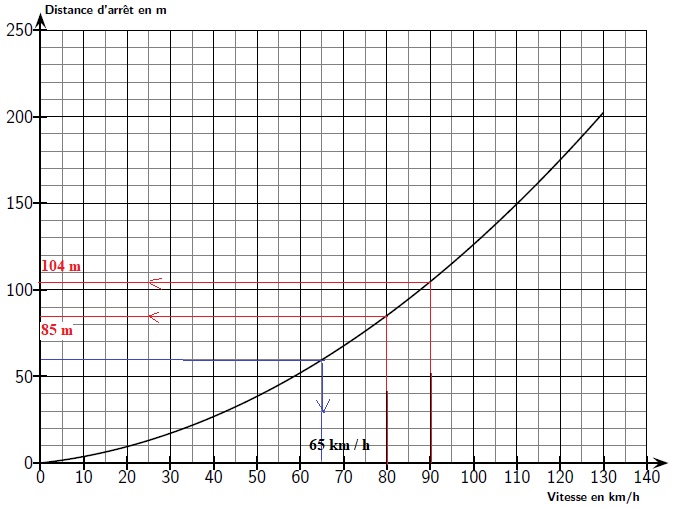
Partie B : Sur route humide.
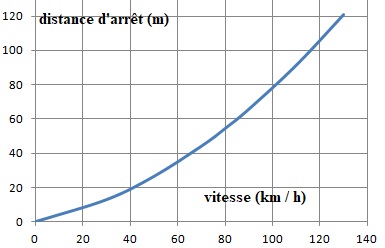
Le graphique suivant, représente la distance d’arrêt en mètres d’un véhicule sur route humide en fonction de la vitesse en km/h.
En s’aidant du graphique, et en faisant apparaîıtre les traits utiles à
la lecture, déterminer avec la précision que permet la lecture
graphique :
1. la distance d’arrêt en mètres d’un véhicule automobile roulant à une vitesse de 80 km/h puis à une vitesse de 90 km/h ;
2. la vitesse en km/h correspondant à une distance d’arrêt de 60 mètres.
Partie C : Sur route sèche
Sur route sèche, la distance d’arrêt en mètres d’un véhicule roulant à
x km/h est modèlisée par la fonction f de la partie A définie
uniquement sur [0; 130] par f(x) = 0,005x(x + 56).
1. Calculer f(80). Interpréter ce résultat dans le contexte de l’exercice.
f(80) = 0,005 x80 ( 80+56) =54,4.
A 80 km / h, la distance d'arrêt est de 54,4 m.
2. Compléter le tableau de valeurs de la fonction f. Arrondir les valeurs à l’unité.
x
|
0
|
30
|
50
|
70
|
80
|
90
|
110
|
130
|
f(x)
|
0
|
13
|
27
|
44
|
54
|
66
|
91
|
121
|
3. Tracer la courbe représentative Cf de la fonction f sur l’intervalle [0 ; 130].
Partie D :
Une campagne publicitaire de la Sécurité Routière du mois de juin 2018
affirme que baisser la vitesse sur les routes de 90 km/h à 80 km/h
permet de gagner 13 mètres au moment du freinage.
En utilisant les résultats des parties B et C,
1. peut-on dire que cette affirmation est vérifiée sur route humide ? Justifier la réponse.
104-85 = 19 m, supérieur à 13 m. Affirmationvraie
2. Peut-on dire que cette affirmation est vérifiée sur route sèche ? Justifier la réponse.
66-54 = 12 m, inférieure à 13 m. Affirmation fausse.
|
....
|
Exercice 2 (5 points)
Partie A :
Un sondage est menée auprès de clients d’un magasin de téléphonie
mobile ayant acheté un téléphone (et un seul) de modèle A ou de modèle
B, avec deux choix de forfaits possibles :
forfait M : « Internet mobile 10 Go » ou forfait S :« Internet mobile 50 Go ».
Le téléphone de modèle A coûte moins cher que le téléphone de modèle B
et le coût du forfait M est moins élevé que celui du forfait S.
Sur les 2 000 clients sondés, 1 040 ont souscrit un forfait M et 1 350 ont acheté un téléphone de modèle B.
On relève également que 30% des sondés ayant acheté un téléphone de modèle B ont souscrit un forfait M.
1. A l’aide des données précédentes, compléter le tableau croisé d’effectifs.
|
Nombre de sondés ayant
souscrit le forfait S
|
Nombre de sondés ayant
souscrit le forfait M |
Total
|
Nombre de sondés ayant
acheté le téléphone A
|
15
|
635
|
650
|
Nombre de sondés ayant
acheté le téléphone B |
1350-405=945
|
1350 x0,30 =405
|
1350
|
Total
|
960
|
1040
|
2000
|
2. Quelle est la fréquence des sondés ayant souscrit un forfait S ?
960 / 2000 =0,48.
3. (a) Quelle est la fréquence des sondés qui ont acheté un téléphone de modèle A et ont souscrit un forfait M ?
635 / 2000=0,318.
(b) L’affirmation suivante du directeur de cette agence est-elle vraie ?
« Moins d’un tiers des sondés choisit la formule la plus économique ».
635 / 2000 =0,3175 valeur inférieure à 0,333. l'affirmation est vraie.
4. Si on choisit au
hasard un client parmi les sondés qui ont répondu avoir souscrit un
forfait S, est-il vrai qu’il y a une très forte probabilité qu’il ait
acheté un téléphone de modèle B ?
645 / 960 = 0,984. Afirmation vraie.
Partie B :
Dans un autre magasin de téléphonie mobile, une enquête de satisfaction
proposée à chaque client a donn´e les résultats suivants :
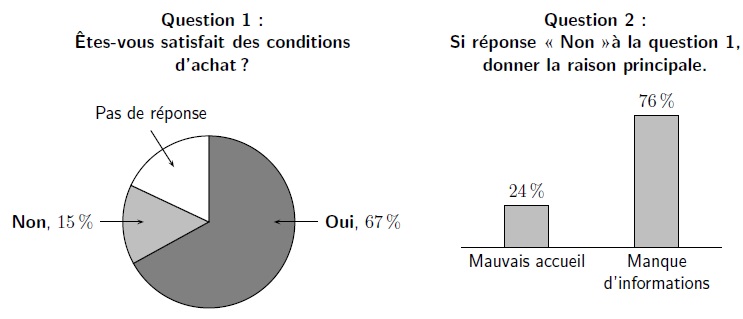
1. Quelle est la proportion, exprimée en pourcentage, de clients interrogés qui n’ont pas répondu à la première question ?
100 -67 -15 = 18 % ( 0,18).
2. Parmi l’ensemble
des clients interrogés, quelle est la proportion, exprimée en
pourcentage, de ceux qui ne sont pas satisfaits des conditions d’achat
en raison d’un mauvais accueil ?
0,15 x 0,24 =0,036 ( 3,6 %).
|
Exercice 3. 5 points.
Lise
a créée une page sur un réseau social pour partager des photos de
voyage. D’après les statistiques de fréquentation des premières
semaines, elle considère qu’on peut modéliser l’évolution du nombre de
personnes intèressées par ses photos par une augmentation de 8% chaque
semaine.
Au moment de la création de la page, le nombre de personnes intèressées était de 150. On note u(n)
le nombre de personnes intèressées par les photos, selon le modèle
considéré par Lise, n semaines apr`es la création de la page. Les
premières valeurs, arrondies à l’unité, de la suite u ainsi définie
sont données dans le tableau ci-dessous, extrait d’une feuille de
calcul.
|
A
|
B
|
C
|
D
|
E
|
F
|
1
|
n
|
0
|
1
|
2
|
3
|
4
|
2
|
u(n)
|
150
|
162
|
175
|
189
|
|
1. Calculer la valeur de u(4). Arrondir à l’unité.
189 x1,08 ~204.
2. Quelle formule,
destinée à être recopiée vers la droite, peut-on saisir dans la cellule
C2 pour obtenir les valeurs de la suite u ?
=1,08*B2
3. Quelle est la nature de la suite u ? Justifier.
On passe d'un terme au suivant en le multipliant par 1,08. Donc suite géométrique de raison 1,08 et de premier terme150.
4. Recopier et
compléter le script ci-dessous de la fonction python nommée
nombre_interesses renvoyant la valeur u(n) pour un entier naturel n
choisi au départ.
d e f n omb r e i n t e r e s s e s ( n ) :
u =150
f o r i i n r ang e ( n ) :
u =u x1,08
r e t u r n u
Ali a démarré en même temps que Lise le partage de photos de ses
propres voyages. Pour les premières semaines, il a représenté sur le
graphiquesuivant le nombre v(n) de personnes intéressèes par ses photos
n semaines après la création de la page. On considère que l’évolution
du nombre de personnes intèressées se poursuit de la même
façon.
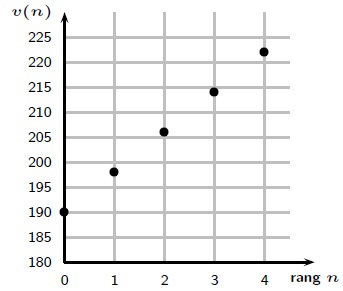
5. (a) Pourquoi peut-on conjecturer que la suite v est arithmétique ?
On passe d'un terme au suivant en lui ajoutant 8. Les points sont alignés.
(b) On admet que v est arithmétique et on donne les deux premiers termes de la suite v : v0=190 ; v1 = 198.
Ecrire une relation entre v(n+1) et v(n) pour tout entier naturel n et calculer les valeurs de v(2), v(3) et v(4).
v(n+1) = v(n) +8.
v(2) = 198 +8 = 206 ; v(3) = 206 +8=214 ; v(4) = 214 +8 = 222.
6. Est-il possible qu’à un moment donné, il y ait davantage de personnes intèressées par les photos de Lise que par celles d’Ali ?
u(n) = 150 x1,08n ; v(n) = 190 +8 n.
u(n) > v(n) ; 150 x1,08n >190 +8 n ;
pour n = 10 : u(10) ~324 ; v(10) = 270. Réponse oui.
|
|
|