Mathématiques,
bac STL Biotechnologie Nlle Calédonie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1. 6 points.
Une certaine quantité de pénicilline est injectée dans le sang d’un patient.
On suppose que l’injection est instantanée et que la vitesse de son
élimination est proportionnelle à la quantité restant dans le sang.
On note t le temps écoulé, en minute, après injection de la
pénicilline, et f (t ) la quantité, en milligramme, de pénicilline
présente dans le sang à l’instant t .
La fonction f , ainsi définie, est solution de l’équation différentielle (E) : y′ = −0,04y.
Dans cet exercice, la quantité de pénicilline injectée est
inconnue,mais on sait que le sang du patient contenait 3,03 mg de
pénicilline, 40 minutes après injection.
Tous les résultats seront arrondis à 0,01 près.
Partie A – Solution de l’équation différentielle.
1. Donner l’ensemble des solutions de l’équation différentielle (E) définies sur [0 ; +∞[.
f(t) =A e-0,04t avec A une constante.
2. Déterminer l’unique solution f définie sur [0 ; +∞[, de l’équation différentielle (E) qui vérifie f (40) = 3,03.
f(40) = 3,03 = A exp(-0,04 x40) =0,2019 A ; A = 3,03 / 0,2019 ~15.
f(t) =15 e-0,04t .
Pour la suite de l’exercice, on prendra f (t )= 15e−0,04t .
Partie B – Étude de la fonction f.
1. Quelle est la quantité de pénicilline initialement injectée dans le sang du patient ?
f(0) = 15 mg.
2. a. Déterminer la fonction dérivée f ′ de la fonction f .
f '(t) = 15 x(-0,04) e−0,04t = -0,6 e−0,04t .
b. Étudier les variations de la fonction f sur l’intervalle [0 ; +∞[.
e−0,04t est positif, f ' (t) est strictement négative. f(t) est strictement décroissante.
c. Déterminer la limite de f(t) en plus l'infini.
Quand t tend vers plus l'infini, e−0,04t tend vers zéro.
3.
Déterminer, par le calcul, la durée pendant laquelle la quantité de
pénicilline dans le sang sera strictement supérieure à 0,1 mg.
15 e−0,04t > 0,1 ; e−0,04t > 0,1 / 15 ; -0,04t > ln(0,1 / 15) ;
0,04 t < ln (150) ; t < ln(150) / 0,04 ; t < 125 minutes.
Partie C – Quantité moyenne de pénicilline.
L’utilisation d’un logiciel de calcul formel nous donne les résultats suivants :
f (t ) = 15 exp(−0.04t )
Intégrale ( f,0,30) ~262,05.
1. Démontrer, par le calcul, ce résultat.
Primitive de f(t) : F = 15 /(-0,04) exp(−0.04t ) = -375exp(−0.04t ).
F(30)-F(0)= -375( exp(-0,04 x30) -1) ~262,05.
2.
La quantité moyenne de pénicilline dans le sang du patient pendant les
30 premières minutes peut être obtenue grâce à l’expression suivante :
(F(30) -F(0) ) / 30.
Déterminer la quantité moyenne de pénicilline présente dans le sang du patient étudié lors des 30 premières minutes.
262,05 / 30~8,74 mg.
|
...
|
|
Exercice 2. (5 points)
Partie A – Présentation de l’étude.
Un objet est vidéoprojeté, en trois dimensions, à une distance comprise
entre 2 et 10 mètres. L’expérience, étudiée dans cet exercice, consiste
à demander à une personne d’estimer la distance à laquelle se trouve
l’objet.
Les résultats sont consignés dans le tableau ci-dessous.
Distance réelle en m ( xi)
|
2
|
2,5
|
3
|
3,5
|
4
|
5
|
6
|
7
|
8
|
10
|
Distance perçue en m (yi)
|
1,9
|
2,4
|
2,8
|
3,3
|
3,7
|
4,3
|
4,7
|
5
|
5,4
|
6
|
1. Quelle remarque peut-on faire sur la perception des distances ?
Les distances perçues sont inférieures aux distances réelles.
2. Représenter le nuage des points de coordonnées (xi ; yi ).
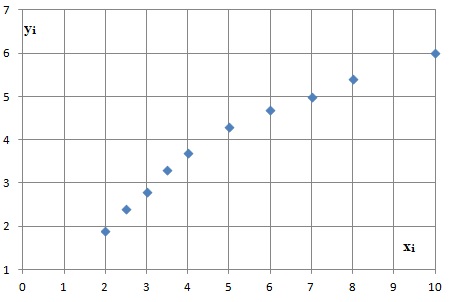
Partie B – Étude d’un premier modèle : la loi de Stevens.
1. On pose ti = ln(xi ) et zi = ln(yi )
a. Compléter le tableau donné en annexe. On arrondira les valeurs à 0,1 près.
ti
|
0,7
|
0,9
|
1,1
|
1,3
|
1,4
|
1,6
|
1,8
|
1,9
|
2,1
|
2,3
|
zi
|
0,6
|
0,9
|
1
|
1,2
|
1,3
|
1,5
|
1,5
|
1,6
|
1,7
|
1,8
|
b. Déterminer, à
l’aide de la calculatrice, une équation de la droite d’ajustement de z
en t par la méthode des moindres carrés sous la forme z = at +b. Les
coefficients a et b seront arrondis à 0,01 près.
z =0,72 t +0,22.
2. À l’aide de la question précédente, déterminer une relation entre y et x sous la forme y = a exp(ßx) où les
coefficients a et ß seront arrondis à 0,01 près.
ln(y) = 0,72 ln(x) +0,22 ; ln(y) = ln(x0,72) +0,22 ;
ln(y) - ln(x0,72) =0,22 ; ln (y / x0,72) = 0,22 ;
y / x0,72 = e0,22 ; y = e0,22 x0,72.
Dans la suite de cette partie, on prendra la relation : y = 1,25 x0,72.
Cette relation est appelée loi de Stevens.
La courbe d’équation y = 1,25 x0,72 est donnée.
3. Selon ce modèle, déterminer la distance réelle, arrondie à 0,1mètre, à laquelle serait placé un objet perçu à 7m.
7 = 1,25 x0,72 ; 7 / 1,25 = x0,72 ; ln(7 / 1,25) =0,72 ln(x) ;
ln(x) = ln(7 / 1,25) / 0,72 ~2,39 ; x ~10,9 m.
Partie C – Étude d’un second modèle : le modèle logarithmique inspiré de la loi de Fechner
Le modèle logarithmique propose une autre relation entre la distance
perçue et la distance réelle. Dans la situation étudiée, on a :
y = 2,6 ln(x)+0,1.
1. Tracer la courbe d’équation y = 2,6 ln(x)+0,1.
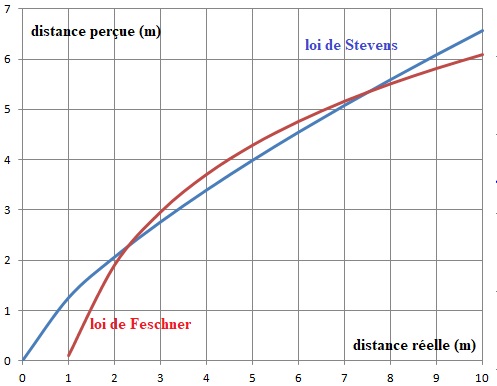
2. Comparer les deuxmodèles. Argumenter votre réponse.
Les deux modèles donnent des résultats concordants pour des distances réelles comprises entre 2 m et 9 m.
3. Selon ce modèle, déterminer la distance réelle, arrondie à 0,1 mètre, à laquelle serait placé un objet perçu à 7 m.
7 = 2,6 ln(x) +0,1 ; 6,9 / 2,6 = 2,65 = ln (x) ; x = e2,65 ~14,2 m.
|
....
|
Exercice 3. 5 points.
La
farine de blé est classée selon des « types » définis en fonction du
taux de cendres, c’est-à-dire en fonction du taux de minéraux présents
dans la farine.
Cette teneur en matière minérale est obtenue en brûlant de la farine et
en rapportant la masse du résidu de cendres à la masse de farine brûlée.
L’exercice porte sur l’étude de la production de la farine complète (
taux de cendre compris entre 1 et 1,2 %) d’une minoterie (établissement
dans lequel sont préparées les farines de céréales).
Tous les résultats seront arrondis à 0,001 près.
Les parties A et B peuvent être traitées indépendamment.
Partie A – Loi normale.
Soucieuse de la qualité de la production de sa farine complète, la
minoterie décide de procéder à un contrôle du taux de cendres. Celui-ci
consiste à choisir au hasard un paquet de farine, à en prélever 100 g,
à le brûler et enfin à en mesurer la masse de cendres. Le paquet est
considéré comme conforme si le taux de cendres est compris entre 1 et
1,2 %.
1. Montrer que le
paquet de farine complète de la production est conforme si la masse du
résidu de cendres est comprise entre 1000 mg et 1200 mg.
1000 mg = 1 g : 1 / 100 = 0,01 soit 1 %.
1200 mg = 1,2 g : 1,2 / 100 = 0,012 soit 1,2 %.
2. On note Y la
variable aléatoire qui, à un prélèvement de 100 g d’un paquet de
farine, associe la masse du résidu obtenu en mg. On admet que Y suit la
loi normale d’espérance 1100 et d’écart-type 40.
Déterminer la probabilité qu’un paquet pris au hasard dans la production de farine complète soit conforme.
P(Y < 1000) =0,0062 ; P(Y < 1200) =0,9938 ; P(1000 < Y <1200) = 0,9938-0,0062 =0,9876 ~0,988.
3. La minoterie
affirme que sa production ne contient pas plus de 5% de paquets de
farine complète non conformes. Or, lors d’un contrôle qualité sur un
échantillon de 150 paquets, on observe 10 paquets de farine complète
non conformes.
a. Indiquer si les conditions n >30, np >5 et n(1−p) >5 sont satisfaites.
150 > 30 ; np = 150 x0,95 ~ 142 > 5 ; 150(1-0,95) =7,5 > 5.
Les conditions sont satisfaites.
b. Déterminer
l’intervalle de fluctuation asymptotique à 95% de la fréquence de
paquets de farine complète non conformes dans un échantillon de 150
paquets prélevés.
1,96 (0,95 x0,05) / 150)½ ~0,035.
Intervalle de fluctuation : [0,05 -0,035 ; 0,05 +0,035] soit [0,015 ; 0,085 ].
c. Énoncer la règle
de décision sur l’hypothèse selon laquelle 5% des paquets de farine
complète de la minoterie sont non conformes.
Fréquence observée 10 / 150 ~0,0667.
d. Conclure sur l’affirmation de la minoterie.
0,0337 appartient à l'intervalle précédent, l'affirmation est conforme.
Partie B – Loi binomiale.
On admet que 5% des paquets de la production de farine complète ne sont
pas conformes. On choisit, au hasard, un lot de 100 paquets de farine
complète dans la production. On admet que la production est
suffisamment importante pour que ce choix puisse être assimilé à un
tirage avec remise de 100 paquets. On note X la variable aléatoire qui,
à tout lot de 100 paquets de type T110, associe le nombre de paquets non
conformes.
1. Justifier que X suit une loi binomiale dont on précisera les paramètres.
Les tirages sont indépendants les uns des autres. Chaque tirage conduit
à 2 issues : paquet conforme q =0,95 ; paquet non conforme p = 0,05.
n = 100 ; p = 0,05. Espérance np = 5.
2. Calculer la probabilité qu’il y ait exactement 2 paquets non conformes.
P(X = 2) = 0,081.
3. Calculer la probabilité qu’il y ait exactement 96 paquets conformes.
1-P(X = 4) = 1-0,178=0,822.
4. a. Calculer P(X < 3) et interpréter le résultat dans le contexte de l’exercice.
P(X =0) = 0,00592 ; P(X =1) =0,03116 ; P(X =2) =0,08112 ; P(X =3) =0,1396.
P(X < 3) =0,2578 ~0,258.
La probabilité qu'il y ait au plus 3 paquets non conformes sur un lot de 100 est 0,258.
b. En déduire P(X >4).
P(X >4) = 1 -P(X < 3) = 1-0,2578 ~0,742.
|
Exercice 4. 4 points.
La consommation finale brute d’énergie représente la consommation
totale d’énergie sur une année, elle est exprimée en
tonnes-équivalent-pétrole : TEP.
En France, la part des énergies renouvelables dans la consommation finale brute d’énergie a progressé
Part des énergies renouvelables dans la consommation finale brute d’énergie (en %)
en 2015 :15,2 ; en 2016 : 16,52.
La directive 2009/28/CE du Parlement européen relative à la promotion
de l’utilisation de l’énergie produite à partir de sources
renouvelables définit pour chaque pays de l’Union européenne l’objectif
à atteindre concernant la part des énergies renouvelables dans la
consommation finale brute d’énergie.
L’objectif de la France est d’atteindre une part d’énergies renouvelables dans la consommation finale brute de 30% en 2023.
Tous les résultats seront arrondis à 0,01 près.
Partie A –Modélisation à partir de 2015.
À partir de 2015, la part des énergies renouvelables dans la
consommation finale brute d’énergie augmente environ de 8,7 % par an.
On désire modéliser la situation par une suite (un), un représentant la part des énergies renouvelables en (2015+n). Ainsi u0 = 15,2.
1. a. Justifier que u1 ≈ 16,52 .
u1=u0 x1,087 =15,2 x1,087=16,52.
b. Calculer u2 et interpréter le résultat dans le contexte de l’exercice.
u2=u1 x1,087 =16,52 x1,087=17,96.
La part des énergies renouvelables en 2017 représentera 17,96 % de la consommation finale brute d’énergie.
2. Justifier que la suite est géométrique. Préciser son premier terme et sa raison.
On passe d'un terme au suivant, en le multipliant par 1,087.
Raison q = 1,087 ; premier terme u0 = 15,2.
3. Donner, pour tout entier naturel n, l’expression de un en fonction de n.
un = u0 x1,087n=15,2 x1,087n.
4. En déduire la part des énergies renouvelables dans la consommation finale brute d’énergie en 2020.
n =5 ; u5 =15,2 x1,0875=23,07 %.
5. a.
Déterminer à partir de quelle année la part des énergies renouvelables
dans la consommation finale brute d’énergie dépassera 30% (justifier en
explicitant la méthode utilisée).
b. L’objectif fixé à la France par cette directive est-il atteint ? Justifier votre réponse.
15,2 x1,087n > 30 ; 1,087n > 30 / 15,2 ; 1,087n >1,9736.
n ln(1,087) > ln(1,9736) ; n > 8,15 soit n > 9. ( année 2024).
L'objectif sera atteint en 2024 et non pas en 2023.
6. a. À l’aide de la calculatrice, déterminer une valeur approchée du terme de la suite (un) correspondant à l’année 2038.
n = 23 ; u23 = 15,2 x1,08723 =103,54 %, impossible, valeur supérieure à 100 %.
b. Que peut-on en déduire sur la viabilité de ce modèle à long terme ?
Ce modèle n'est pas valide à long terme ; la limite de la suite doit être 100 %.
Partie B – L’objectif pour 2035.
L’objectif
fixé par l’Union européenne est qu’en 2035 la part des énergies
renouvelables soit de 40%. On estime qu’à partir de 2015 la part des
énergies renouvelables dans la consommation finale brute d’énergie doit
augmenter de 28% tous les cinq ans.
On considère l’algorithme suivant :
u←15,2
Pour n allant de 1 à 4
u←u ×1,28
Fin Pour
1. Quelle est la valeur de la variable u à la fin de l’exécution de l’algorithme ?
u1 =15,2 x1,28 =19,456 ; u2 =19,456 x1,28 =24,904 ; u3 =24,904 x1,28 =31,877 ; u4 =31,877 x1,28 =40,8.
2. Interpréter ce résultat compte tenu de l’objectif fixé pour la France en 2035.
L'objectif de la France sera atteint.
|
|
|

