L'odyssée du futur, à bord du premier navire à hydrogène autour du monde, bac STI2D SPCL Antilles  2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . ...... ..... Partie A : le soleil comme source d'énergie A.1  Citer au moins deux particularités des panneaux solaires équipant Energy Observer. Les panneaux sont galbés pour épouser la forme de la coque.; Certains panneaux sont bifaces pour recueillir les rayons solaires directs et indirects par réverbération sur la coque et les flots. Cetains sont recouverts d'un revêtement antidérapant, compatible avec le passage des équipiers. Les ingénieurs ont optés pour la basse tension et une connectique évitant tout risque électrique. A.2.1 Décrire la structure d'une onde électromagnétique. Une onde électromagnétique comporte un champ magnétique et un champ électrique oscillant à la même fréquence. Ces deux champs périodiques et de même fréquence sont perpendiculaires l’un à l’autre ainsi qu’à la direction de propagation de l’onde. A.2.2 Une onde électromagnétique monochromatique est caractérisée par sa longueur d'onde l. Citer une autre grandeur physique caractérisant cette onde et préciser son unité. La fréquence exprimée en hertz ( Hz). A.3 Fonctionnement d'une cellule photovoltaïque. A.3.1 Compléter le bilan énergétique d'une cellule photovoltaïque. 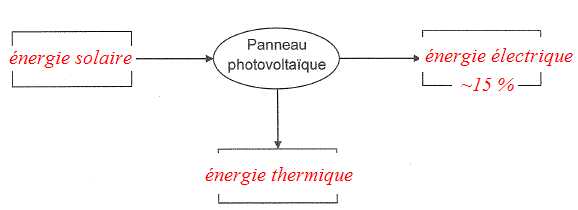A.3.2 Déterminer l'énergie minimale Emini en joule que doit pôsséder un photon pour que la cellule produise un courant électrique. Pour le silicium monocristallin, Emini = 1,10 eV ou 1,10 x1,60 10-19 =1,76 10-19 J. A.3.3 Exprimer la relation donnant l en fonction de Emini et nommer les constantes physiques qui y figurent. l = h c /Emini. h : constante de Planck ; c : célérité de la lumière dans le vide. A.3.4 Montrer par le calcul que l = 1,13 10-6 m. lmaxi = 6,63 10-34 x3,00 108 / (1,76 10-19) =1,13 10-6 m. A.3.5 Déterminer le domaine auquel appartiennent ces ondes. Proche infrarouge. A.3.6 Justifier l'utilisation du silicium comme semi-conducteur adapté au domaine du visible. Longueeur d'onde du domaine visible [ 4 10-7 m ; 8 10-7 m], valeurs inférieures à 1,13 10-6 m. A.4.1 Montrer qu'il serait possible d'installer 77 panneaux Bisun Protect 290 pour équiper la surface de 130 m2 du bateau. Longueur d'un panneau : 1,675 m ; largeur : 1,001 m ; surface : 1,675 x1,001 ~1,68 m2. 130 / 1,68 ~77. En 2018, Energy Observer a fait le tour de la Méditerranée. L'ensoleillement moyen y est de 1000 W m-2. A.4.2 Calculer la puissance lumineuse absorbée par l'ensemble des panneaux. 1000 x 130 =1,3 105 W. A.4.3 Donner l'expression du rendement et calculer le rendement maximal de cette installation. Puissance électrique maximale / puissance solaire absorbée x 100 = 77 x 290 x100 / (1,3 105) ~ 17 %. A.4.4 Ce rendement est-il excellent, convenable, faible ou très faible ? Ce rendement est faible. ... Partie B : l'hydrogène, un vecteur énergétique B.1.1 L'hydrogène possède trois isotopes. Définir ce terme. Deux isotpes ne diffèrent que par leur nombre de neutrons. Ils possèdent le même numéro atomique. B1.2 Le tritium est un isotope radioactif de l'hydrogène. Il se désintègre avec émission d'un rayonnement ß-. B.1.2.1 Quelle est la particule émise lors de ce rayonnement. Un électron. B.1.2.2 Déterminer A et Z. Identifier X. 31H ---> AZX +0-1e. Conservation de la charge : 1 = Z-1 ; Z = 2, élément hélium 32He. Conservation du nombre de nucléons : 3 = A. B.1.2.3 Donner la définition de l'activité A d'une source radioactive et préciser son unité. L'activité d'une source radioactive est le nombre de désintégrations par seconde. Elle s'exprime en becquerel ( Bq). B.1.2.4 Donner deux raisons pour lesquelles la présence de tritium ne présente pas de danger pour l'homme ou pour l'environnement. Très faible abondance ; l a particule émise ß- est très peu pénétrante. B.2. Fonctionnement de la pile à combustible. B.2.1 Préciser quelle électrode est le siège d'une oxydation. Justifier. 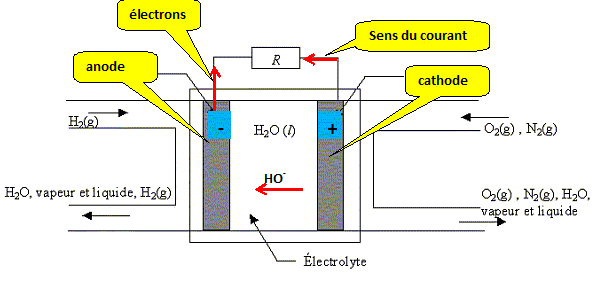A l'anode négative le dihydrogène est oxydé. Cette oxydation s'accompagne de la libération d'électrons. H2(g) ---> 2H+aq + 2e-. B.2.2 Ecrire la demi-équation se déroulant à la cathode. Quel nom qualifie ce type de réaction ? Réduction du dioxygène : ½O2 (g) + 2H+ aq + 2e- ---> H2O(l) B.2.3 Ecrire l'équation de fonctionnement de la pile. H2(g) ---> 2H+aq + 2e-. ½O2 (g) + 2H+ aq + 2e- ---> H2O(l) Ajouter et simplifier. ½O2 (g) +H2(g) ---> H2O(l).  L'ensemble des réservoirs peut contenir 62 kg de dihydrogène. B.2.4 Exprimer puis calculer la quantité de matière de dihydrogène disponible lorsque les réservoirs sont pleins. n = masse de dihydrogène / M(H2) =62 103 / 2 = 3,1 104 mol. B.2.5 Déterminer la quantité de matière d'électrons qui circule dans le circuit extérieur si on consomme la totalité du dihydrogène. H2(g) ---> 2H+aq + 2e-. n(e-) = 2 n = 6,2 104 mol. B.2.6 En déduire la quantité d'électricité totale débitée par la pile. Q = F n(e-) = 96500 x 6,2 104 =5,983 109 ~6,0 109 C. B.2.7 Choisir en justifiant la démarche, la relation à appliquer pour calculer l'énergie électrique E, disponible lorsqu'on mesure une tension U aux bornes de la pile E = Q / U ; E =  U / Q ; E = Q U. Une énergie ( J) est une tension ( V) fois une quantité d'électricité ( C). B.2.8 Si U = 1,3 v, montrer que E = 7,8 109 J. E = 1,3 x 5,983 109 ~7,8 109 J. B.2.9 L’essence sera assimilée à de l'octane. Calculer le volume d'essence susceptible de libérer cette énergie. Pouvoir calorifique inférieur de l'octane PCI = 44,4 MJ kg-1 ; masse volumique de l'octane r = 0,703 kg / L. E / (PCI r ) avec r = 703 kg m-3. 7,8 109 /(44,4 106 x 703)~0,25 m3 ou 250 L. B.3.1 Montrer que la quantité de matière d'octane contenue dans 250 L d'essence vaut environ 1,5 103 mol. M(octane) = 114 g / mol. n = masse d'octane / M(octane) = 250 x703 / 114 ~1,5 103 mol. B.3.2. Compléter l'équation de la combustion de l'octane. C8H18 + 12,5 O2 ---> 8 CO2 + 9 H2O. B.3.3. Montrer que la quantité de matière de dioxyde de carbone émise par la combustion de 250 L d'essence vaut environ 1,2 104 mol. n(CO2 ) = 8 xn(octane) = 8 x1,5 103 =1,2 104 mol. B.3.4. En déduire la masse de dioxyde de carbone rejeté. 1,2 104  x M(CO2) = 1,2 104 x44 =5,28 105 g ~5,3 102 kg. B.3.5. En déduire le bilan carbone ( g / km) si le bateau avait consommé de l'essence. L'essence confère au bateau une autonomie de 5 jours à une vitesse de 6,0 noeuds. 1 noeud = 1,85 km / h. Distance parcourue : 6 x1,85 x24 x5 =1332 km. 5,3 105 / 1332 ~4,0 102 g / km .... Partie C: Propulsion du bateau. La propulsion du bateau est assurée par deux moteurs électriques d'une puissance de 45 kW chacun avec une vitesse de rotation pouvant atteindre 3000 tours / minute. Une voile de kite surf de 50 m2 équipe le bateau. C.1. Etude du capteur de vitesse. 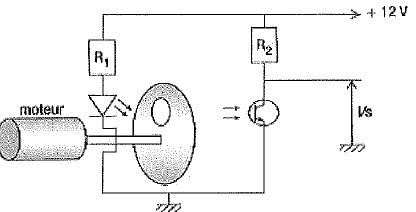C.1.1 Quelles sont les grandeurs d'entrée et de sortie du capteur ? Vitesse ou fréquence de rotation en entrée ; tension en sortie. C.1.2 Déterminer la fréquence de rotation du moteur en Hz puis en tour / minute. 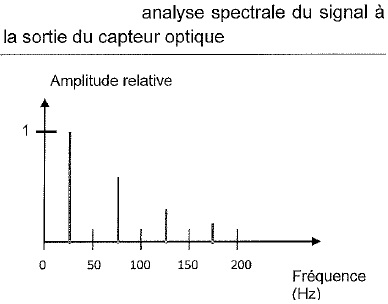Fréquence du fondamental : 25 Hz ou 25 tours / seconde ou 25 x60 = 1500 tours / minute. C.1.3. Le schéma suivant confirme t-il le résultat précédent ? 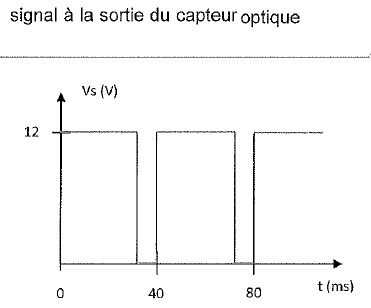Période : 40 ms = 0,04 s ; fréquence 1/0,04 =25 Hz ; donc confirmation. C.1.4 Quelle est la valeur de la fréquence du second pic ? A quelle harmonique correspond-t-elle ? f = 75 Hz = 3 x25 Hz ( 3ème harmonique). C.2.Le bateau est soumis à 4 forces lors de son déplacement. son poids P, la poussée d'Archimède, les forces de frottements f ( air et eau ) et la force motrice F. Lorsque son rythme de croisière est atteint, le bateau se déplace à la vitesse constante de 11,1 km / h. C.2.1 Calculer le poids du bateau. Masse m = 33 tonnes. P = mg = 33 103 x9,81 ~3,2 105 N. C.2.2. Sans calcul, montrer que la poussée d'Archimède vaut 3,2 105 N. A vitesse constante le poids et la poussée d'Archimède se compensent.. C.2.3 En supposant que la trajectoire du bateau est rectiligne uniforme, que peut-on dire de la résultante des forces qui s'exrcent sur le bateau ? D'après la première loi de Newton, la résultante des forces est nulle. L'équipage décide d'utiliser l'aile géante de kite surf. La voile exerce une force de traction T dont la composante horizontale, dans la direction du mouvement, vaut 750 N. On souhaite connaître la vitesse que peut atteindre le bateau lorsque la voile fournit un effort sur une distance D = 150 m. C.2.4 Justifier que le travail du poids et de la poussée d'Archimède sont nuls. Le poids et la poussée d'Archimède étant perpendiculaires à la vitesse, ces forces ne travaillent pas. C.2.5 Sans calcul, montrer que la somme des travaux des forces horizontales f et F est nulle. La résultante des forces P, Poussée, f et F éatnt nulle, la somme des travaux de ces forces est nulle. C.2.6. Exprimer puis calculer le travail de T pendant les 150 premiers mètres. W =  T D = 750 x 150 = 1,125 105 ~1,13 105 J. C.2.7 En appliquant le théorème de l'énergie cinétique, montrer que la vitesse atteinte après 150 m de traction par la voile est de 14,5 km / h. ½m v2finale - ½mv2initiale = W. v2finale =2 W / m +v2initiale =2,25 105 /(33 103) +(11,1 / 3,6)2 =6,82 +9,51=16,3. vfinale = 4,04 m /s ou 4,04 x3,6 ~14,5 km / h. .

menu