Les
petites Curie, des voitures radiologiques,
bac Sti2D et STL ( biotechnologies) Métropole 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
PARTIE A : Des rayons X pour examiner les blessés
L’équipage de chaque « petite Curie », est constitué d’un médecin, d’un
manipulateur et d’un chauffeur. Chaque véhicule est équipé de tout le
matériel de radiologie nécessaire à savoir : un appareil à rayons X, du
matériel photographique pour développer les clichés, des rideaux, des
écrans et des paires de gants destinées à protéger les mains des manipulateurs.
A.1. Énergies des rayons X
· Énergie E en Joule (J) transportée par un photon de fréquence n en hertz (Hz) : E = h · n
· constante de Planck : h = 6,63 × 10-34 J · s
· célérité de la lumière dans le vide : c = 3,00 × 108 m · s-1
· électron-volt : 1 eV = 1,60 × 10-19 J
A.1.1. Les rayons X font partie des ondes électromagnétiques.
A.1.1.1. Montrer que la fréquence maximale n des rayons X produits dans le tube est de l’ordre de 3 x 1019 Hz.
Les énergies des photons X sont comprises approximativement entre 120 eV et 120 keV.
E = 1,6 10-19 x 120 000 =1,92 10-14 J.
n = E / h =1,92 10-14 / (6,63 10-34) =2,9 1019 Hz.
A.1.1.2. En déduire la longueur d’onde λ correspondant à ces rayons X.
l = c / n = 3,00 108 / (2,9 1019) =1,0 10-11 m.
A.1.1.3.
La longueur d’onde d’un photon UVA présent dans le rayonnement solaire
est d’environ 380 nm. Montrer que son énergie est environ 37000 fois
plus faible que celle d’un photon X produit par le tube.
380 nm = 3,8 10-7 m ; 1,0 10-11 / (3,8 10-7) =2,7 10-5~ 1 / 37 000.
A.1.1.4. Justifier la nécessité pour les manipulateurs radio de l’époque d’utiliser des gants de radioprotection.
Les rayons X sont bien plus dangereux pour la santé que les UVA. Une protection est indispensable.
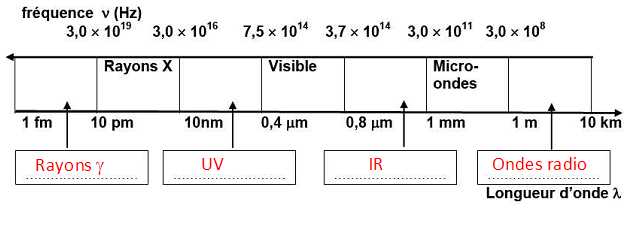
A.1.2. Attribuer à
chaque domaine le type de rayonnement correspondant : visible,
ultra-violet, infrarouge, rayonnement X et rayonnement gamma.
 A.1.3. Déterminer l’énergie cinétique d’un électron soumis à une tension accélératrice U = 100 kV.
A.1.3. Déterminer l’énergie cinétique d’un électron soumis à une tension accélératrice U = 100 kV.
Ec = e U = 1,6 10-19 x1,0 105 = 1,6 10-14 J.
A.1.4. On suppose
que lors de l’impact de l’électron sur la cible, la totalité de son
énergie cinétique est absorbée par un atome de tungstène de la cible
avant d’être réémise sous forme d’un photon. Montrer que ce dernier
correspond bien à un photon X.
n = E / h =1,6 10-14 / (6,63 10-34) =2,4 1019 Hz.
l = c / n = 3,00 108 / (2,4 1019) =1,2 10-11 m = 12 pm, cette valeur appartient bien au domaine des photons X.
A.2. Atténuation des rayons X
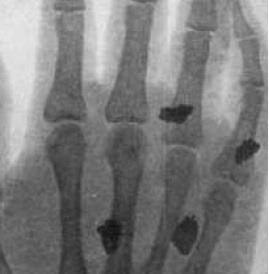
A.2.1. Que peut-on
dire des numéros atomiques Z des éléments chimiques constituant les
éclats d’obus utilisés pendant la « Grande Guerre » ?
Les éclats sont constitués de fer, élément chimique à numéro atomique élevé.
Le fer absorbe donc bien plus les rayons X que les os ou les tissus mous. Les éclats apparaissent plus foncé sur les clichés.
A.3. Élévation de température dans le tube à rayons X
La puissance tube est la puissance électrique nécessaire à l’obtention,
avec une tension électrique accélératrice U, d’un faisceau d’électrons
d’intensité de courant I.
A.3.1. Soit un
cliché obtenu avec une tension accélératrice U = 100 kV. L’intensité de
courant du faisceau d’électrons étant de I = 300 mA, déterminer la
puissance tube.
P = U I = 1,0 0105 x 0,300 =3,00 104 W.
A.3.2. Le temps de
pose d’un cliché étant de 2,00 s, montrer que l'énergie transférée à
l'anode lors de ce cliché s’élève à Ecliché = 6,00 × 104 J.
E =Puissance ( W) fois durée (seconde) =3,00 104 x2,0 = 6,0 104 J.
A.3.3. L’anode est constituée d’une cible de tungstène de masse m = 1,00 kg et de capacité calorifique massique cm = 133 J · kg-1 · K-1.
Exprimer, puis calculer, l’élévation de température, ΔT de la cible
lors du fonctionnement du tube en supposant que toute l’énergie
transférée par le faisceau à l’anode sert à élever sa température.
E = m cm DT ; DT =E / (m cm) = 6,0 104 / 133=451 °C.
|
.
|
|
PARTIE B : De l’électricité pour alimenter le tube à rayons X.
B.1. Alimentation du tube.
Pour alimenter le tube à rayons X, on pouvait installer dans les
voitures radiologiques, soit un groupe électrogène, soit une « dynamo »
encore appelée génératrice de courant continu et entraînée par le
moteur de la voiture.
B.1.1. Donner deux avantages qu’apportait la « dynamo » par rapport à un groupe électrogène de l’époque.
Un groupe électrogène est lourd et encombrant, contrairement à une dynamo.
Enfin une dynamo est moins chère..
B.1.2. Donner les deux principaux inconvénients de l’utilisation de la « dynamo ».
La dynamo nécessite le fonctionnement de la voiture, d'où la consommation d'essence.
B.2. Bilan de puissance de la « dynamo »
B.2.1. Donner la
valeur de l’intensité du courant continu délivré par la « dynamo »
utilisée dans les « petites Curie » ainsi que la valeur de la tension
correspondante.
110 V et 15 A.
B.2.2. Exprimer puis calculer la valeur de la puissance électrique Pélec fournie par la « dynamo » aux récepteurs qu'elle alimente.
Pélec = U I = 110 x 15 =1,65 103 W = 1,65 kW.
B.2.3. Sachant que
seulement 80% de la puissance mécanique fournie à la « dynamo » sont
convertis en puissance électrique donner l’expression de la puissance
mécanique fournie à la « dynamo » Pméca et montrer qu’elle vaut Pméca = 2,1 kW.
Pméca = 1,65 / 0,80 ~2,1 kW.
B.2.4. Compléter le schéma simplifié de la conversion de puissance qui a lieu dans la « dynamo » en utilisant les termes
suivants : « dynamo », puissance électrique, puissance thermique, puissance mécanique.
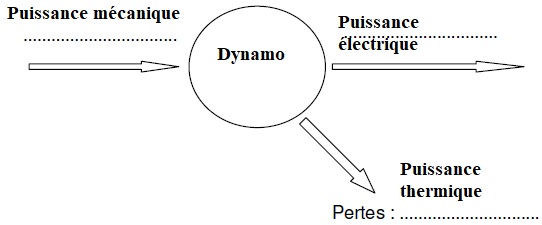
B.2.5. En déduire la valeur de la puissance totale dissipée Pdiss.
Pdiss = 2,1 -1,65 = 0,45 kW.
B.2.6. Une partie
de la puissance dissipée est due à l’effet Joule. Donner une autre
cause possible de la dissipation de puissance dans la « dynamo ».
Frottements mécaniques.
.
B.2.7. La vitesse de rotation du moteur qui entraîne la « dynamo » vaut 1800 tours par minute.
Données :
· Puissance mécanique Pméca du moteur en watt (W) : Pméca = C · w.
· C : moment du couple en N · m
· w : vitesse de rotation du moteur en rad · s-1.
B.2.7.1. Exprimer la valeur de la vitesse de rotation w du moteur en rad · s-1.
w =1800 x2 x3,14/ 60 ~188 rad s-1.
B.2.7.2. Déterminer la valeur du moment du couple C de la « dynamo ».
C = Pméca / w =2,1 103 / 188 ~11 N m.
B.2.7.3. Indiquer comment le conducteur pouvait régler la vitesse de rotation du moteur de la voiture radiologique.
Le conducteur disposait d'un voltmètre.
|
|
|
|
B.3 Évaluation du volume d’essence nécessaire à une heure consécutive de prise de cliché.
Données :
· masse volumique du carburant, r carburant = 0,703 kg · L-1.
· puissance mécanique Pméca fournie à la « dynamo » lors de la prise d’un cliché, Pméca = 2,1 kW.
· énergie libérée Elib par unité de masse de carburant, Elib = 4,79 × 107 J · kg-1.
· volume du réservoir d’une petite Curie, Vrés = 35,0 L.
B.3.1. En supposant
que seulement 10% de l’énergie libérée lors de la combustion de
l’essence sert à entraîner la « dynamo », évaluer le volume d’essence
nécessaire lors d’une durée de fonctionnement de l’appareillage
radiographique de 1h.
Energie mécanique fournie à la dynamo : Pméca fois durée = 2,1 x3600 =7,56 103 kJ.
Energie fournie par la combustion de l'essence : 10 x7,56 103 = 7,56 104 kJ.
Masse de carburant : 7,56 107 / (4,79 107) =1,58 kg.
Volume d'essence : 1,58 / 0,703 ~2,25 L.
B.3.2. En
déterminant l’autonomie d’utilisation d’une « petite Curie » en
radiographie, justifier l’affirmation " la dépense d'essence
relativement élevée".
Autonomie : 35,0 / 2,25 = 15,6 heures, valeur inférieure à une journée.
PARTIE C : Un moteur à essence comme source d’énergie.
Dans les « petites Curie », le moteur, qui permet de faire fonctionner
la voiture quand elle est en mouvement et la dynamo quand elle est à
l’arrêt, est un moteur à essence.
On assimilera l’essence à de l'octane de formule moléculaire C8H18.
C.1. Réaction de combustion de l’octane
C.1.1. Recopier et ajuster l'équation de la réaction de combustion complète de l'octane dans l’air, donnée ci-dessous :
2 C8H18 (ℓ) + 25O2 (g)--->16 CO2(g) + 18 H2O(ℓ)
C.1.2. Donner la signification de deux des pictogrammes de sécurité fournis pour l’octane.

C.2. Masse de dioxyde de carbone rejeté
C.2.1. Déterminer, à l’aide des données fournies, la quantité de matière d'octane noctane contenue dans 1,00 L d'essence.
Masse / masse molaire = 703 / (8 x12 +18) = 6,17 mol.
C.2.2. En déduire que la quantité de matière n(CO2) de dioxyde de carbone, rejetée lors de la combustion d’un litre d'essence, vaut 49,4 mol.
6,17 x 8 = 49,3 mol.
C.2.3. Calculer la masse m(CO2) de dioxyde de carbone rejetée pour 1,00 L d'essence. On donne la masse molaire M(CO2) du dioxyde de carbone : 44,0 g · mol-1.
49,3 x44 =2,17 103 g = 2,17 kg.
C.2.4. Le réservoir du moteur des « petites Curie » peut contenir 35,0 L d’essence et l’autonomie de ces voitures est de 270 km.
C.2.4.1. Calculer la masse totale mtot de dioxyde de carbone libérée par la combustion de la totalité de l’essence contenue dans le réservoir.
2,17 x 35 ~76 kg.
C.2.4.2. En déduire la masse m de dioxyde de carbone libérée par kilomètre parcouru.
76 / 270 =0,28 kg ou 280 g.
C.2.4.3. Qu’en serait-il du malus écologique d’une « petite Curie » compte tenu des normes établies en 2017 ?
10 000 €.
|
|
.
|



