Production
autonome d'énergie électrique,
bac Sti2D et STL ( SPCL) Métropole 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Partie A : Irrigation des cultures
(9 points)
Objectif :
faire correspondre la production d’énergie électrique locale (partie
A.2) aux besoins du système d’irrigation du village (partie A.1).
A.1) Dimensionnement des besoins.
A.1.1) On cherche à
déterminer la consommation d'eau journalière V (en m3·j-1)
nécessaire à l’irrigation.
Compléter le tableau qui permet d'estimer les besoins totaux en eau.
Utilisation
|
Surface à cultiver
(ha)
|
consommation
journalière (m3 / ha)
|
consommation
journalière totale
|
m3
|
litre
|
| riziculture |
3
|
30
|
90
|
90
000
|
autres
cultures
|
0,5
|
5
|
2,5
|
2
500
|
verger
|
0,7
|
10
|
7
|
7
000
|
| Total |
99,5
|
99
500
|
On
souhaite pomper l’eau nécessaire grâce à une pompe alimentée en direct
par des panneaux solaires. Le réservoir est situé à 25 m au-dessus du
cours d'eau. La durée d’ensoleillement journalière est de 8 h, la pompe
ne peut fonctionner que pendant cette durée.
A.1.2) Déterminer
le débit q de la pompe en m3.h-1 puis en L.s-1
permettant d’assurer le stockage de la quantité d'eau nécessaire à
l’irrigation pendant une journée.
99,5 / 8 = 12,4375 ~12,4 m3 h-1; 12 400 / 3600
=3,45 L / s.
La puissance de pompage est donnée par la relation :
P = qm g H
· P : puissance en watt (W)
· g : accélération de pesanteur (g = 9,81 m·s-2)
· H : hauteur de pompage (m)
· qm : débit massique (kg·s-1)
A.1.3) Dans la
pratique, le débit massique de la pompe est de 3,40 kg·s-1,
calculer la puissance P nécessaire au pompage.
P = 3,40 x9,8 x25 =833 W.
A.1.4) Calculer la
puissance du moteur électrique Pe de la pompe ; le rendement
du dispositif de pompage est de 70 %.
Pe = 833 / 0,70 =1190 W = 1,19 kW.
A.2) Dimensionnement de
l’installation solaire.
On relie le moteur électrique de la pompe à un panneau photovoltaïque
chargé de l’alimenter.
Afin de déterminer le nombre de cellules photovoltaïques nécessaires à
cette alimentation électrique, des essais en laboratoire sont réalisés.
On utilise des projecteurs halogènes pour éclairer la cellule
photovoltaïque.
L’irradiance (puissance lumineuse surfacique) reçue par la cellule
solaire est réglée telle que E = 1000 W·m-2. Dans le
laboratoire, la température de la cellule est de TC = 25°C.
A.2.1) On dispose
de la cellule solaire, d'un ampèremètre, d'un voltmètre et d'une
résistance réglable.
Proposer un montage qui permet de retrouver la caractéristique du
courant I en fonction de la tension U de la cellule solaire.
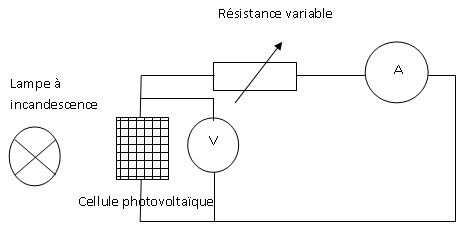 A.2.2)
La notice de l’ampèremètre utilisé indique que « ΔI = 1 % de la valeur
lue + 3 d ». On rappelle que « d » désigne le dernier digit ou la
résolution.
A.2.2)
La notice de l’ampèremètre utilisé indique que « ΔI = 1 % de la valeur
lue + 3 d ». On rappelle que « d » désigne le dernier digit ou la
résolution.
Calculer la valeur de ΔI lorsque l’ampèremètre indique la valeur I =
3,52 A.
ΔI =3,52 x0,01 +3 x0,02 =0,095
~0,1 A
A.2.3) En vous aidant des
caractéristiques de la cellule, calculer la puissance lumineuse reçue
par la cellule Pcell (en W) au cours de notre
expérimentation.
Largeur de la cellule : 660 mm ; longueur 1477 mm. Surface : S = 1,477
x0,66 =0,97482 m2.
Puissance lumineuse reçue : Pcell =1000 x0,97482 ~975 W.
Dans les conditions de l’essai de laboratoire, on trouve une puissance
maximale Pmax fournie par la cellule de 35 W.
A.2.4) Quel est le
rendement de la cellule photoélectrique ?
35 / 975 ~0,036 ( 3,6 % ).
Ce rendement est très faible. Nous souhaitons comparer cette puissance
effectivement mesurée à celle qui est prévue par le constructeur.
A.2.5) Identifier
la caractéristique correspondant aux conditions expérimentales et
calculer la puissance maximale Pm en utilisant le document
constructeur.
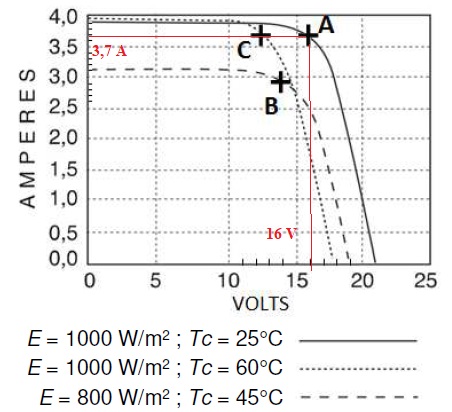
Pm = 16 x3,7 =59,2 W.
A.2.6) En
exploitant le document A3, calculer l’énergie du photon pour laquelle
la réponse spectrale est maximale. On rappelle que c = 3.108
m/s et que h = 6,62.10-34 J·s.
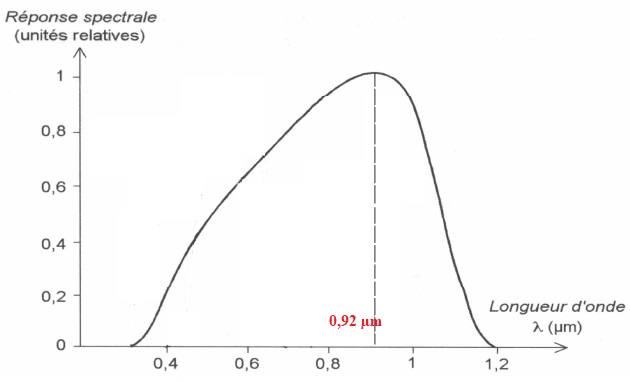
E = hc / l = 6,62 10-34
x 3,0 108 /(0,92 10-3) =2,16 10-19 J.
A.2.7) Proposer une
explication possible à la différence observée entre la mesure au
laboratoire et les données du constructeur qui correspondent à une
utilisation en lumière naturelle.
Le maximum du spectre de la lumière émise par la lampe ne correspond
pas à 0,92 µm.
Après avoir refait des essais au soleil qui correspondent aux
conditions moyennes rencontrées à Madagascar (irradiance de E = 800 W·m-2
; température de 45°C), on trouve que la puissance maximale d’une
cellule de Pmax = 42 W.
A.2.8) Le moteur
électrique consomme une puissance Pe = 1200 W. Déterminer le
nombre de cellules ncell composant le panneau photovoltaïque
pour assurer le fonctionnement de la pompe.
1200 / 42 = 28,57 ~29 cellules.
A.2.9) Actuellement
le village utilise une pompe fonctionnant avec un moteur à essence.
Citer au moins deux avantages que procurerait son remplacement par le
panneau photovoltaïque.
Pas de dégagement de CO2 ; pas de souci de s'approvisionner
en essence.
A.3) Contrainte de pression.
A.3.1) La pompe choisie est capable d’imposer à sa sortie une surpression ΔPS
de 6 bars par rapport à la pression atmosphérique. Cette valeur
est-elle suffisante pour assurer le relevage de l’eau de la rivière
vers le réservoir ?
On justifiera la réponse par un calcul.
Données : masse volumique de l’eau : ρeau = 1 000 kg·m-3 ; 1 bar = 105 Pa.
DP = ρeau g H = 1000 x9,81 x25 =245 250 Pa ~2,5 bars, valeur inférieure à 6 bars.
La pompe est capable de remplir le réservoir.
A.3.2) En réalité,
lorsque de l’eau circule dans les tuyaux, il existe une perte de
pression due aux frottements de l’eau sur le tuyau (effet de viscosité)
qui diminue donc la hauteur maximale de relevage. Sur le terrain la
hauteur de relevage maximale obtenue avec les 6 bars en sortie de pompe
est en réalité de 47 m. Calculer cette perte de pression.
1000 x9,81 x47 =461 070 Pa ~4,6 bars,
Perte de pression 6 -4,6 =1,4 bars.
|
.
|
|
Partie B : Éclairage autonome (6 points)
La nuit tombe généralement vers 18 heures. On souhaite que les
habitants puissent disposer d’une source de lumière, notamment pour que
les enfants puissent réaliser leurs devoirs.
L'objectif de cette partie est d’étudier l’opportunité d’installer des lampes à gravité dans les maisons.
En descendant, le sac de 12 kg entraine un générateur produisant de
l’énergie électrique permettant d’alimenter la lampe LED du dispositif.
B.1) Énergie récupérable grâce à la gravité
Donnée : valeur de l’intensité de la pesanteur g = 10 N·kg-1.
B.1.1) Calculer la valeur du poids du sac.
P=mg = 12 x10 = 120 N.
La masse descend à vitesse constante d’une hauteur h = 2 m sur une durée Dt = 15 minutes.
B.1.2) À partir des données précédentes, calculer la variation de l’énergie potentielle Ep du sac au cours de son mouvement.
DEp = mgh = 12 x10 x2 = 240 J.
B.1.3) Estimer
l'énergie cinétique du sac et montrer que seule une fraction
négligeable de l'énergie potentielle est transformée en énergie
cinétique.
Vitesse moyenne du sac : 2 / (15 x60) =2,22 10-3 m /s ; Ec = ½mv2 =60 x(2,22 10-3)2 ~3,0 10-4 J.
3,0 10-4 / 240 x100 =1,2 10-4 %.
B.1.4) Montrer que la valeur de la puissance mécanique moyenne récupérable pendant la chute est de l'ordre de 0,27 W.
DEp / Dt =240 /(15 x60) ~0,27 W.
B.2) Etude du convertisseur mécanique-électrique.
B.2.1) Compléter le bilan de puissance en précisant la forme énergétique des puissances considérées.
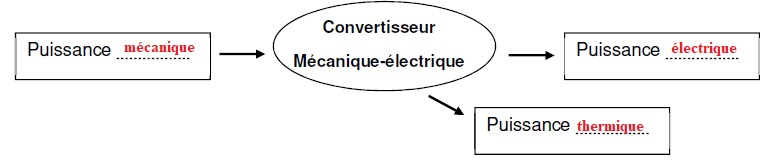
B.2.2) À l’aide des caractéristiques du générateur électrique données, déterminer le rendement η du convertisseur.
Tension : 2,6 V ; intensité : 0,070 A ; vitesse 2190 tour / minute.
Puissance électrique : U I = 2,6 x0,070 = 0,18 W ; rendement = 0,18 / 0,27 = 0,67.
B.3) Choix du type d’éclairage.
B.3.1) Justifier que la lampe à gravité utilisant une LED est la meilleure solution en remplacement d’une bougie traditionnelle.
Flux lumineux d'une bougie : 12 lm
La LED, alimentée sous 2,6 V, fournit le même flux lumineux que la bougie.
|
Flux lumineux
|
Tension alimentation
|
courant électrique
|
puissance consommée
|
efficacité lumineuse
|
LED
|
11 lm
|
2,6 V
|
67 mA
|
175 mW
|
63 lm / W
|
lampe à incandescence
|
1 lm
|
2,6 V
|
0,005 A
|
0,13 W
|
8 lm / W
|
lampe éco fluocompacte
|
1200 lm
|
230 V
|
87 mA
|
20 W
|
60 lm/ W
|
..
..
|
B.4) Transmission.
La masse suspendue entraine par une courroie crantée un tambour de diamètre 7 cm.
B.4.1) Quelle est la vitesse de rotation ω du tambour exprimée en tour/minute ?
w = v / (0,5 d) = 2,22 10-3 / (3,5 10-2) =6,34 10-2 rad / s ou 6,34 10-2 x2 p ~0,4 tour /s ou 0,4 x60 = 24 tours / minute.
B.4.2) À quoi servent les engrenages.
Ils permettent de modifier la vitesse de rotation.
|
|
|
|
Partie C : Le cuiseur économe (5 points)
Des actions de reboisement sont engagées au sein du village, l'objectif
de cette partie est d’étudier une solution permettant de réduire la
consommation de bois.
Données :
Masse volumique de l’eau : ρeau = 1 000 kg·m-3
Masses molaires : MC = 12 g·mol-1 ; MH = 1 g·mol-1 ; MO = 16 g·mol-1
Capacité thermique massique de l’eau : ceau = 4180 J·kg-1·K-1
Pouvoir calorifique du bois sec (correspond à l'énergie récupérée lors
de la combustion d'un kilogramme de bois sec) : q = 1,8.107 J.kg-1.
C1) Étude de la réaction chimique d’une combustion.
Dans cette partie, on fera l'hypothèse que les molécules organiques
constitutives du bois sont principalement des polymères du glucose
comme la cellulose.
C.1.1) Identifier le motif de la cellulose. Donner la formule brute de ce motif.
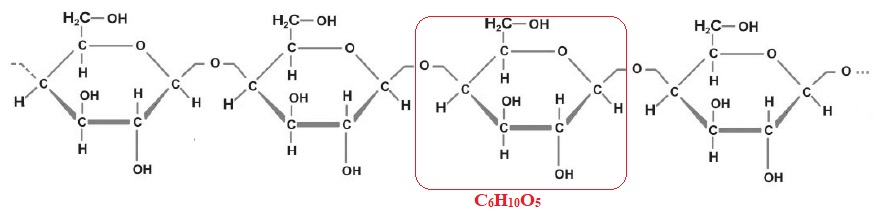
C.1.2) Écrire puis équilibrer l’équation de combustion complète de la molécule C6H10O5.
C6H10O5 + 6O2 --> 6CO2 +5H2O.
On peut estimer que lors de la combustion de 1 tonne de cette molécule, il y a consommation d’environ 740 m3 d'O2, et production simultanée d’environ 740 m3 de CO2 et 560 kg d'eau.
C.1.3) Après avoir calculé les masses molaires du C6H10O5 et de l’eau, vérifier qu’une tonne de C6H10O5 produit par combustion approximativement 560 kg d’eau.
M(C6H10O5) = 6 x 12 +10 +5 x16 = 162 g / mol. M(H2O) = 2+16 = 18 g / mol.
n(C6H10O5) = 1,0 106 / 162 = 6172,8 mol ;
n(eau) = 5 n(C6H10O5) =5 x6172,8 = 30864,2 mol
Masse d'eau : 30864,2 x18 =5,55 105 g ~555 kg.
C2) Chauffage pour les besoins domestiques
On souhaite étudier les besoins en bois pour chauffer de l’eau.
C.2.1) On souhaite chauffer 10 litres d’eau. Calculer l’énergie nécessaire Qeau pour amener l’eau de 20°C à 100°C.
Qeau = m ceau Dq = 10 x4180 x(100-20)=3,34 106 J.
C.2.2) En faisant l'hypothèse qu'il n'y a aucune perte, quelle est la masse de bois théorique mbth à brûler ?
q / Qeau = 3,34 106 /(1,8.107 ) =0,18 kg..
Pour la suite des questions, on considère que la masse de bois nécessaire est mbois = 0,2 kg.
C.2.3) Evaluer la masse de bois réellement consommée pour chauffer les 10 L d’eau :
· Pour le foyer ouvert : mfo (en kg), rendement 10 % : mfo =0,2 x10 = 2 kg.
· Pour le poêle rocket : mpr (en kg) ; rendement 50 % : mpr = 0,2 /0,5= 0,4 kg.
C.2.4) Donner au moins deux arguments permettant d’expliquer le meilleur rendement d’un poêle Rocket.
Faible inertie thermique du foyer de combustion ;
Une isolation du foyer avec des cendres évite les déperditions latérales.
Le paravent augmente l’efficacité de l’échange avec la casserole.
|
|
.
|




