Mathématiques, bac Sti2d et STL 2019 Antilles

Mathématiques, bac Sti2D et STL ( SPCL) Antilles 2019.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

Exercice 1 ( 4 points).
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n’est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l’absence de réponse ne rapportent ni n’enlèvent aucun point.
1. Pour tout réel a strictement positif, [ln(2a +ln(8a) ] / 2 est égal à :
a. ln(4a) vrai ; b. ln(5a) ; c. ln(16a) ; d. ln(8a²).
[ln(2a +ln(8a) ] / 2 = 0,5 ln(2a x 8a) = 0,5 ln(16a²)= ln[(16a²)^½ ]= ln(4a).

2. On considère une fonction f définie et dérivable sur ]0; +∞[. On appelle C sa courbe représentative dans un repère orthonormé.
On admet quela limite en zéro de f est moins l'infini et que la limite de f(x) en plus l'infini est plus l'infini.
La courbe C admet :
a. deux asymptotes parallèles à l’axe des ordonnées,
b. une asymptote parallèle à l’axe des ordonnées et une asymptote parallèle à l’axe des abscisses,
c. une asymptote parallèle à l’axe des ordonnées et aucune asymptote parallèle à l’axe des abscisses, Vrai.
Asymptote verticale d'équation x = 0.
d. deux asymptotes parallèles à l’axe des abscisses.

3. On considère le nombre complexe z = -2e^{i p /4}.
Une écriture du nombre complexe conjugué de z est :
a. 2e^{i p /4} vrai . b. 2e^{-i p /4}. c. 2 2e ^{-i 5p /4}. d. 2 e ^{i 5p /4}.
z =2e^{i p /4} e^{-i p /2}=2e^{-i p /4} ;
nombre complexe conjugué de z : 2e^{i p /4} .

4. Le plan complexe est muni d’un repère orthonormé . Les droites d’équationy = x ety = -x partagent le plan en quatre zones comme indiqué ci-dessous :

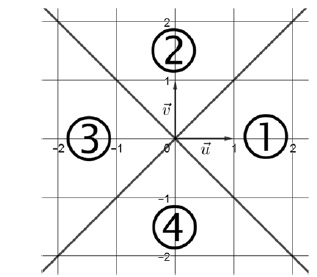
Soit z un nombre complexe non nul. On sait que :
 la partie réelle de z est strictement inférieure à sa partie imaginaire ;
 un argument de z est strictement compris entre 3p /4 et 2p.
Le point image de z se situe :
a. dans la zone 1 ; b. dans la zone 2 ; c. dans la zone 3 vrai d. dans la zone 4 .

.

Exercice 2 ( 7 points ).
L’énergie houlomotrice est obtenue par exploitation de la force des vagues. Il existe différents dispositifs pour produire de l’électricité à partir de cette énergie. Les installations houlomotrices doivent être capables de résister à des conditions extrêmes, ce qui explique que le coût actuel de production d’électricité par énergie houlomotrice est élevé.
On estime qu’en 2018 le coût de production d’un kilowattheure (kWh) par énergie houlomotrice était de 24 centimes d’euros. C’est nettement plus que le coût de production d’un kilowattheure par énergie nucléaire, qui était de 6 centimes d’euros en 2018.
On admet qu’à partir de 2018 les progrès technologiques permettront une baisse de 5% par an du coût de production d’un kilowattheure par énergie houlomotrice.
Les deux parties de cet exercice peuvent être traitées de manière indépendante.
Partie A.
Pour tout entier naturel n, on note C_n le coût de production, en centime d’euro, d’un kilowattheure d’électricité produite par énergie houlomotrice pour l’année 2018 +n. Ainsi, c₀= 24.
1. a. Calculer c₁. Interpréter le résultat dans le contexte de l’exercice.
c₁ = 0,95 c₀ = 0,95 x24 =22,8.
En 2019 le coût de production d’un kilowattheure (kWh) par énergie houlomotrice est de 22,8 centimes d’euros.
b. Déterminer la nature de la suite (u_n) et donner ses éléments caractéristiques.
Le rapport de deux termes consécutifs est constant. Il s'agit d'une suite géométrique de raison 0,95 et de premier terme c₀ = 24.
c. Pour tout entier naturel n, exprimer c_n en fonction de n.
c_n = c₀ x0,95ⁿ = 24 x0,95ⁿ.
2. Résoudre dans l’ensemble des entiers naturels l’inéquation 0,95ⁿ < 0,25.
La fonction logarithme étant stricttement croisante sur R*+ :
n ln(0,95 ) < ln(0,25) ; n < ln(0,25) / ln(0,95) ; n > 27.
3. Dans cette question, on admet que le coût de production d’un kilowattheure par énergie nucléaire reste constant et égal à 6 centimes d’euros.
Déterminer l’année à partir de laquelle le coût d’un kilowattheure produit par énergie houlomotrice deviendra inférieur au coût d’un kilowattheure produit par énergie nucléaire.
24 x 0,95ⁿ < 6 ; 0,95ⁿ < 6 / 24 ; 0,95ⁿ < 0,25 ; n > 27. ( année 2018+27 = année 2045 ).
4. Dans cette question, on estime que le coût de production d’un kilowattheure par énergie nucléaire va augmenter tous les ans d’un centime d’euro. On souhaite alors déterminer l’année à partir de laquelle le coût d’un kilowattheure produit par énergie houlomotrice deviendra inférieur au coût d’un kilowattheure produit par énergie nucléaire.
a. Recopier et compléter l’algorithme suivant afin que la valeur de la variable N en sortie d’algorithme permette de répondre au problème.
C ← 24
D ← 6
N ← 2018
Tant que C > D…
C ← 0,95 C
D ← D+1
N ← N+ 1
Fin Tant que
b. Répondre au problème posé. Aucune justification n’est demandée.

Année
2019
2020
2021
2022
2023
2024
2025
2026
2027
2028

Coût kWh produit par la houle C
22,8
21,66
20,577
19,548
18,57
17,64
16,76
15,92
15,126
14,37

Coût kWh nucléaire D
7
8
9
10
11
12
13
14
15
16

C > D
vrai
vrai
vrai
vrai
vrai
vrai
vrai
vrai
vrai
faux.

...
..

Partie B.
On admet que la durée de vie d’un composant électronique d’une installation houlomotrice, exprimée en année, est une variable aléatoire X qui suit la loi exponentielle dont le paramètre est l= 0,04 .
1. Déterminer la durée de vie moyenne de ce composant électronique.
E(X) = 1 /0,04 = 25 ans.
2. On considère la fonction f définie sur l’intervalle [0; +oo[ par f(x) = 0,04 e^{-0,04 t}.
a. Déterminer une primitive F de la fonction f sur l’intervalle [0; +oo[ .
F = -e^{-0,04 t}.
b. Démontrer que p(X < t) = 1- e^{-0,04 t}.
p(X < t) = F(t) - F(0) = -e^{-0,04 t} -(-e⁰) =-e^{-0,04 t} +1 =1- e^{-0,04 t}.
3. a. Calculer P(X > 15). Donner le résultat arrondi à 10^-3 .
P (X >15) = 1-P(X < 15) = e^{-0,04 x15} = e^-0,6 =0,549.
b. Interpréter cette valeur dans le contexte de l’exercice.
La probabilité que ce composant dure plus de 15 ans est 0,549.

Exercice 3. 6 points.
En raison des frottements avec l’atmosphère résiduelle terrestre, les satellites en orbite basse perdent progressivement de l’altitude et finissent par se consumer dans les couches les plus denses de l’atmosphère. Cet événement est appelé rentrée atmosphérique.
Le temps, exprimé en jour, avant la rentrée atmosphérique dépend des caractéristiques du satellite et de l’altitude h, exprimée en kilomètre, de son orbite.
Pour un satellite donné, ce temps est modélisé par une fonction T de la variable h, définie et dérivable sur l’intervalle [0 ; +oo[ .
Les trois parties de cet exercice peuvent être traitées de manière indépendante.
Partie A – Étude d’un premier satellite
On admet que la fonction T, associée à ce premier satellite, est une solution de l’équation différentielle (E) suivante dans laquelle h désigne une fonction de la variable h définie et dérivable sur [0 ; +oo[ et y′ la fonction dérivée de y.
(E) : 40 y' -y = 0.
1. Résoudre l’équation différentielle (E) sur [0 ; +oo[ .
y' -y / 40 = 0 ; y' -0,025 y = 0 ; solution T = A e^{0,025 h} avec A une constante.
2. Déterminer la fonction T solution de l’équation différentielle (E) qui vérifie la condition T(800) = 2000.
2000 = A e^{0,025 x800} = A e²⁰ ; A = 2000 e^-20.
T = 2000e^{0,025 h-20}.

Partie B – Étude d’un deuxième satellite
Dans cette partie, on admet que la fonction T, associée à ce deuxième satellite, est définie sur l’intervalle [0 ; +oo[ par :
T(h) =0,012 K e^0,025(h-150).
Le nombre réel K est appelé coefficient balistique du satellite.
La fonction T associée à ce deuxième satellite est représentée ci-après.
Dans cette partie, on ne demande pas de justification. Les résultats seront donnés avec la précision permise par le graphique.

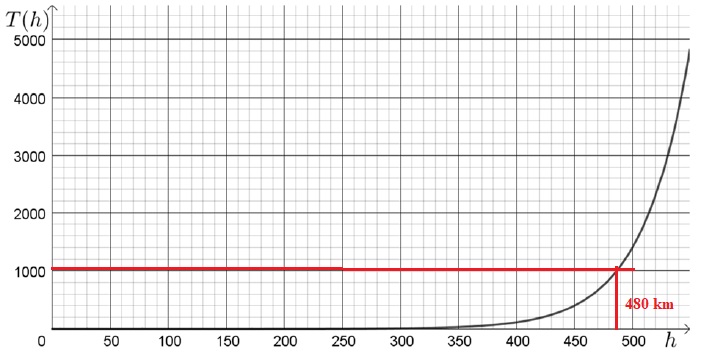
1. À quelle altitude minimale faut-il mettre en orbite ce deuxième satellite pour que le temps restant avant sa rentrée atmosphérique soit au moins égal à 1 000 jours ?
2. Déterminer une valeur approchée du coefficient balistique K de ce deuxième satellite.
1000 =0,012 K e^{0,025(480-150)}=0,12 K e^8,25 ; K = 1000 / (0,12 e^8,25) ~2,18.

Partie C – Étude d’un troisième satellite : Hubble
Le satellite Hubble a un coefficient balistique K égal à 11.
La fonction T, associée à ce troisième satellite, est donc définie sur l’intervalle [0 ; +oo[ par :
T(h) = 0,132 e^{0,025 (h-150)} .
1. L’orbite du satellite Hubble est située à l’altitude h de 575 km. Calculer le temps T restant avant la rentrée atmosphérique du satellite Hubble. Arrondir au jour près.
T(h) = 0,132 e^{0,025 (575-150)} = 5432 jours.
2. Déterminer la limite de T en +oo.
e^{0,025 (h-150)}tend vers plus l'infini quand h tend vers plus l'infini.
T(h) tend vers plus l'infini quand h tend vers plus l'infini.
3. a. Déterminer T '(h) , où T ' désigne la fonction dérivée de T.
T '(h) = 0,132 x0,025 e^{0,025 (h-150)} = 0,0033e^{0,025 (h-150)}.
b. En déduire le sens de variations de la fonction T sur [0 ; +oo[.
e^{0,025 (h-150)} est positif sur [0 ; +oo[. La fonction T est strictement croissante sur cet intervalle.
4. On souhaite étudier l’effet d’une augmentation de 10 km de l’altitude h sur le temps restant avant la rentrée atmosphérique du satellite Hubble.
a. Montrer que T(h+10) = e^0,25 T(h).
T(h+10) = 0,132 e^{0,025 (h+10-150)} =0,132 e^{0,025 (h-150)} e^{0,025 x10}=0,132 e^{0,025 (h-150)} e^0,25= e^0,25 T(h).
b. En déduire qu’augmenter l’altitude h de 10 km revient à augmenter d’environ 28% le temps restant avant la rentrée atmosphérique du satellite Hubble.
T(h+10) -T(h)= e^0,25 T(h)- T(h) = T(h) (e^0,25-1) ;
[T(h+10) -T(h) / ] / T(h) =e^0,25-1=0,284 (~ 0,28 ou 28 %)

Exercice 4 (3 points)
Un atelier de mécanique de précision est équipé de machines à commande numérique permettant la production de pièces métalliques en aluminium.
Un client passe une commande de pièces dont la longueur souhaitée est de 75 millimètres (mm).
Les trois parties de cet exercice peuvent être traitées de manière indépendante.
Les résultats seront arrondis, si nécessaire, à 10^-.2.
Partie A.
Le réglage des machines permet de produire des pièces dont la longueur, exprimée en millimètre, est modélisée par une variable aléatoire X qui suit la loi normale d’espérance
µ = 75 et d’écart-type s =0,03.
Afin de garantir au client une précision optimale, seules les pièces dont la longueur est comprise entre 74,95 mm et 75,05 mm sont jugées commercialisables.
1. Déterminer P(X > 74,97).
P(X >74,97) = 1 -P(X < 74,97) = 1-0,1587 ~0,84.
2. Déterminer la probabilité qu’une pièce prise au hasard soit commercialisable.
P(X < 74,95) =0,0478 ; P(X < 75,05) =0,9522 ;
P(74,95 <X < 75,05) =0,9522 -0,0478 ~0,90.

Partie B.
On souhaite améliorer la précision de la production. Pour cela, les machines sont réglées et reprogrammées. Après réglage, la longueur des pièces, en millimètre, est modélisée par une
variable aléatoire Y suivant une loi normale. Son espérance est inchangée et vaut µ= 75.
La valeur de l’écart-type a été modifiée. On note s′ la nouvelle valeur de l’écart-type.
Ces nouveaux réglages permettent de limiter la proportion de pièces non commercialisables.
On a P(74,95 <Y < 75,05) =0,95 .
Déterminer s′. Justifier.

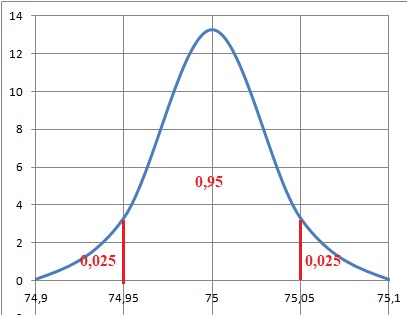
On pose Z = (Y-75) / s'.
P (Z < 75,05) =0,975 ; Z =1,96 = (75,05-75) / s' =0,05 / s'.
s'= 0,05 /1,96 =0,0255.

Partie C.
On procède à de nouveaux réglages.
Le responsable de l’atelier affirme alors être en mesure de commercialiser 97% des pièces.
On procède à un contrôle de qualité en prélevant au hasard 300 pièces métalliques. On constate que 14 d’entre elles ne sont pas commercialisables.
Au seuil de 95%, faut-il mettre en doute l’affirmation du responsable de l’atelier ? Justifier la réponse.
Fréquence observée f = 14 / 300 = 0,0467.
1,96 [ f(1-f) / n ]^½ =1,96 [0,03 (1-0,03) / 300]^½= 0,0193.
Intervalle de fluctuation asymptotique [ 0,03-0,0193 ; 0,03 +0,0193) soit [0,0107 ; 0,0493 ]
0,0467 appartient à cet intervalle. L'affirmation n'est pas remise en cause au risque de 5 %.

.

.

menu