Math�matiques,
bac St2S Polyn�sie septembre 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
|
|
......
.....
|
Exercice 1.
7 points.
Un nutritionniste consulte les fiches de ses patients de l’ann�e 2018
qui suivent tous un r�gime avec ou sans gluten.
Les deux parties du probl�me sont ind�pendantes.
Partie A.
Le nutritionniste fait les trois constats suivants :
• parmi ses patients, il compte 312 femmes ce qui repr�sente 60 % de sa
patient�le ;
• 25 % de ses patients suivent un r�gime sans gluten ;
• parmi ses patients suivant un r�gime avec gluten, 70 % sont des
femmes.
1. a. Justifier que
le nombre total de ses patients s’�l�ve � 520.
312 / 0,60 = 520.
b. En d�duire le
nombre de patients suivant un r�gime sans gluten.
520 x0,25 =130.
c. Compl�ter le
tableau d’effectifssuivant.
Nombre
de patients
|
Femmes
|
Hommes
|
Total
|
qui
suivent un r�gime avec gluten
|
390
x0,7=273
|
208-91=117
|
390
|
qui
suivent un r�gime sans gluten
|
312-273=39
|
130-39=91
|
130
|
Total
|
312
|
520-312=208
|
520
|
2. Dans les
questions suivantes, on exprimera les proportions en pourcentage, et
on arrondira les r�sultats � 0,1 %.
a. Calculer la
proportion d’hommes suivant un r�gime avec gluten dans l’ensemble de la
patient�le.
117 / 520 x100 =22,5 %.
b. Calculer la
proportion de femmes parmi les patients suivant un r�gime sans gluten.
39 / 520 x100 =7,5 %.
Partie B.
Le
nutritionniste isole les fiches de ses patients seniors (plus de 60
ans). Parmi eux, certains, souffrant de troubles cardio-vasculaires,
doivent suivre un r�gime sans sel. Il remarque que :
• parmi ses 200 patients seniors, 96 sont des hommes et 104 sont des
femmes ;
• parmi les hommes seniors, 60 suivent un r�gime sans sel ;
• parmi les femmes seniors, 26 suivent un r�gime sans sel.
Le nutritionniste choisit une fiche au hasard parmi celles des patients
seniors. Chaque fiche a la m�me probabilit� d’�tre choisie.
On consid�re les �v�nements suivants :
- H : � la fiche est celle d’un homme � ;
- F : � la fiche est celle d’une femme �.
- R : � la fiche est celle d’un patient senior suivant un r�gime sans
sel �.
Dans les questions
suivantes, on donnera les valeurs exactes des probabilit�s demand�es.
1. a. V�rifier que
P (H) = 0,48.
P(H) = 96 / 200 =0,48.
b. Recopier et
compl�ter l’arbre pond�r� de probabilit�s ci-dessous.
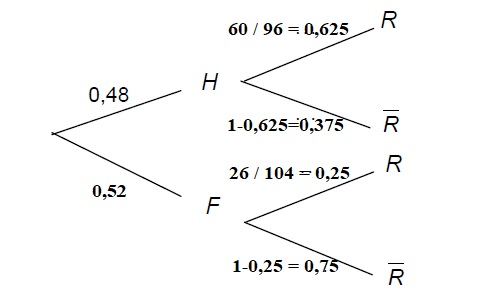
2. a. D�crire par
une phrase l’�v�nement H ∩R , puis calculer P (H ∩R)
Le senior est un homme et il suit un r�gime sans sel.
P (H ∩R) =0,48 x 0,625 =0,30.
b. Montrer que la
probabilit� de l’�v�nement R est �gale � 0,43.
Formule des probabilit�s totales : P (H ∩R) +P
(F ∩R) =0,30 +0,52 x0,25 =0,30 +0,13 = 0,43.
c. Les �v�nements R et H sont-ils
ind�pendants ? Justifier la r�ponse.
P (H ∩R) =0,30 ;
P(H) = 0,48 ; P(R) =0,43 ; 0,48 x0,43 =0,2064 diff�rent de 0,30.
P (H ∩R) diff�re de P(H) x P(R) ; les
�v�nements R et H ne sont pas ind�pendants.
|
...
|
|
Exercice 2.
(5 points)
Cet exercice est un questionnaire � choix multiples (QCM).
Pour chaque question, quatre r�ponses sont propos�es parmi lesquelles
une seule est correcte.
Indiquer sur la copie le num�ro de la question suivi de la r�ponse
choisie. Aucune justification n’est demand�e.
Chaque bonne r�ponse rapporte un point. Aucun point n’est enlev� pour
une absence de r�ponse ou pour une r�ponse inexacte.
La courbe C ci-dessous est la repr�sentation graphique d’une fonction ƒ
d�finie sur l’intervalle [−2;3]. La droite T est la tangente � la
courbe C au point d’abscisse 2.
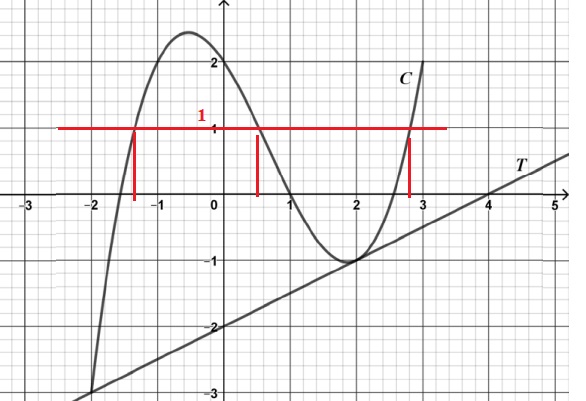
1. L’image de 0
par la fonction ƒ est :
a. 0 ; b. 1 ; c. 2 vrai
; d. 2,58
2. Par la fonction
ƒ, le r�el 1 admet :
a. un ant�c�dent ; b. deux ant�c�dents ;
c. trois ant�c�dents
vrai ; d. aucun ant�c�dent
3. L’in�quation
ƒ(x) < 2 a pour
ensemble de solutions :
a. [−2;−1] ; b. [−1;0] ; c.
[−2;−1]∪[0;3] vrai ; d. {−1; 0 ; 3}
4. On note ƒ' la
fonction d�riv�e de la fonction ƒ sur l’intervalle [−2;3]. Alors :
a. ƒ'(2) = −1 ; b. ƒ'(2) = −2 ; c.
ƒ'(2) = 0,5 vrai ; d. ƒ'(2) = 4
5. La fonction ƒ
est d�finie sur l’intervalle [−2;3] par : ƒ(x) = 0,5x3 − x2
−1,5x + 2 . Alors :
a. ƒ'(−2) = 8,5 vrai
; b. ƒ'(−2) = 9 ; c. ƒ'(−2) = −3 ; d. ƒ'(−2) = 2.
f '(x) = 1,5 x2 -2x-1,5 ; f '(-2) =1,5 x4 +2 x2 -1,5 = 8,5.
|
....
|
Exercice 3. 8 points.
Au sein
d’une entreprise de pr�paration de colis, un m�decin du travail
r�pertorie les maladies et accidents professionnels des salari�s
survenus depuis 2012.
Les deux parties du probl�me sont ind�pendantes.
Partie A :
maladies et accidents professionnels.
En regroupant les maladies et accidents professionnels par ann�e, il
obtient le tableau suivant :
ann�e
|
2012
|
2013
|
2014
|
2015
|
2013
|
2017
|
2018
|
rang
( xi)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
nombre
de maladies et accidents ( yi)
|
243
|
257
|
264
|
277
|
296
|
302
|
314
|
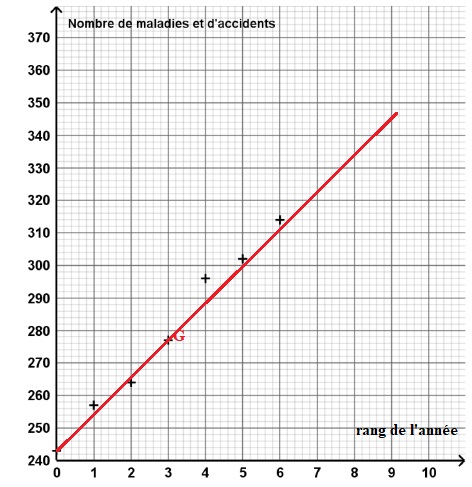
on a repr�sent�, dans un rep�re orthogonal, le nuage de points de
coordonn�es (xi ; yi) associ� � cette s�rie
statistique.
1. Calculer les
coordonn�es du point moyen G du nuage et placer G dans le rep�re
pr�c�dent.
xG =(0 +1 +2 +3 +4 +5 +6) / 7= 3
yG=(243 +257 +264 +277 +296 +302 +314) / 7 =279.
2. On consid�re la
droite D d’�quation : y = 12x + 243 . On admet que cette droite r�alise
un ajustement affine de cette s�rie valable jusqu’en 2025.
a. Tracer la
droite D dans le rep�re en annexe. Indiquer les coordonn�es des points
utilis�s.
Point G et point de coordonn�e (0 ; 243).
b. Selon ce mod�le,
donner une estimation du nombre de maladies et accidents professionnels
en 2022. Justifier la r�ponse.
x = 10 ; y = 12 x10 +243 = 363.
Partie B :
am�liorations des conditions de travail
En fin d’ann�e 2018, la direction a d�cid� de faire appel � un
ergonome, expert en conditions de travail. Celui-ci �tudie
l’organisation de l’entreprise, les cadences de travail et la fa�on de
travailler des salari�s. Il recommande la mise en place de nouveaux
rythmes de travail, des investissements dans des machines pour le
transport de charges lourdes et propose un ensemble de bonnes pratiques
� respecter. Ces consignes sont mises en application � partir du mois
de janvier 2019.
En janvier 2019, on a comptabilis� 26 maladies et accidents
professionnels dans l’entreprise.
L’ergonome estime que le nombre de maladies et d’accidents
professionnels diminuera chaque mois de 6 % � partir de f�vrier 2019.
1. Estimer le
nombre de maladies et d’accidents professionnels attendus par
l’ergonome en f�vrier 2019. Arrondir le r�sultat � l’unit�.
26 x(1-0,06) =26 x0,94 =24,44 ~24.
2. L’ergonome
propose d’estimer le nombre de maladies et d’accidents professionnels
dans les mois � venir � l’aide d’un tableur. Il a commenc� � remplir le
tableau ci-dessous. Les cellules de la ligne 3 sont au format nombre
arrondi � l’unit�.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
1
|
mois
|
janvier
2019
|
f�vrier
|
mars
|
avril
|
mai
|
juin
|
juillet
|
2
|
rang
du mois
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
3
|
nombres
maladies et accidents
|
26
|
|
|
|
|
|
|
Quelle formule entr�e dans la cellule C3, puis recopi�e vers la droite,
permet d’obtenir le nombre de maladies et d’accidents professionnels
dans l’entreprise dans les mois � venir ?
=0,94*B3
3. On mod�lise le
nombre de maladies et d’accidents professionnels ayant lieu le n-i�me
mois apr�s janvier 2019 par une suite (un ). Ainsi u0
= 26 .
a. Quelle est la
nature de la suite (un ) ? Quelle est sa raison ?
On passe d'un terme au suivant en le multipliant par 0,94 ; suite
g�om�trique de raison 0,94 et de premier terme 26.
b. Pour tout
entier n , exprimer un en fonction de n.
un = 26 x0,94n.
c. Calculer le
nombre de maladies et d’accidents professionnels pr�visibles en juillet
2019.
u6 = 26 x0,946 =17,93 ~18.
4. a. R�soudre dans
R l’in�quation : 26�0,94x < 12.
0,94x <
12 /26 ; x ln(0,94) <
ln(12 /26) ; -0,061875 x <
-0,7731 ; x >
0,7731 / 0,061875 ; x >12,49 soit 13.
b. L’ergonome
estime que descendre � 12 maladies et accidents professionnels par mois
est un bon objectif. � partir de quel mois et de quelle ann�e cet
objectif sera-t-il atteint conform�ment au mod�le ?
x = 13 ; fin f�vrier 2020 ou d�but mars 2020.
|
|
