Physique
chimie,
bac St2S Polynésie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1. Imagerie fonctionnelle du corps humain 8 points
1. Orienter l’axe dans le sens des longueurs d’onde croissantes. Placer sur ce même document les rayonnements g.

2. L’isotope 123 I émet un rayonnement g d’énergie 159 keV ou 2,54×10-14 J.
Calculer la longueur d’onde correspondant à ce rayonnement.
Données : h = 6,63×10-34 J·s, c = 3,00×108 m·s-1.
l = hc / E =6,63 10-34 x3,.0 108 / (2,54 10-14)=7,83 10-12 m.
3. Décrire précisément la composition des noyaux d’iode 123I et 131I.
123I : 53 protons et 123-53 =70 neutrons ; 131I : 53 protons et 131 -53 =78 neutrons.
4. Désintégration radioactive de l’iode.
4.1. Rappeler les lois de conservation qui caractérisent les réactions nucléaires.
Conservations de la charge et du nombre de nucléons.
4.2. La désintégration de l’iode 131 est de type ß-. Écrire l’équation de désintégration de l’iode 131, en choisissant le noyau formé dans le tableau suivant :
| Noyau
|
Sb
|
Te
|
I
|
Xe
|
Cs
|
Nombre de protons Z
|
51
|
52
|
53
|
54
|
55
|
13153I --->13154Xe +0-1e.
5. Demi-vie d’un isotope radioactif.
5.1. Définir la période (ou demi-vie) d’un isotope radioactif.
La demi-vie est la durée au bout de laquelle l'activité initiale est divisée par deux.
5.2. Indiquer en justifiant lequel de ces deux isotopes est le plus adapté à l’imagerie médicale.
La période radioactiveemi- (ou dvie) de 123I est de l’ordre de 13 heures, celle du 131I est d’environ 8 jours.
Les noyaux radioactifs sont considérés totalement désintégrés au bout de 20 périodes radioactives (ou demi-vies).
L'iode 123 est le plus adapté. La radioactivité a disparu au bout de 20 x13 = 260 heures ( environ 11 jours).
6. Impact de l’examen sur la santé
6.1. On injecte une dose d’iode 123I
à monsieur X., l’activité vaut 7 MBq au moment de l’injection. L’examen
a lieu trois heures plus tard. À ce moment-là, l’activité de l’iode
est-elle supérieure ou inférieure à 3,5 MBq ? Justifier.
L'activité diminue de manière exponentielle au cours du temps. Trois
heures après l'injection, l'activité est inférieure à 3,5 MBq.
6.2. Pour vérifier
les effets du traitement sur monsieur X., une seconde scintigraphie est
pratiquée six semaines plus tard. Préciser si ce délai est suffisant
pour que le premier examen ne perturbe pas le deuxième. Justifier.
6 semaines = 6 x7 x24 =1008 heures soit environ 1008 / 13 ~77 périodes.
L'activité de la première injection a disparu au bout de 20 périodes.
Le premier examen ne perturbe pas le deuxième.
Le patient doit être perfusé afin de recevoir l’injection du produit iodé.
Données :
Masse volumique du liquide à perfuser : ρliquide perfusé = 1080 kg·m-3
Intensité de la pesanteur terrestre : g = 9,81 N·kg-1
Loi de la statique des fluides : Δp = ρ∙g∙h
Section de la veine en m2 : S = π∙(d /2)2 avec d en m
Le débit volumique Dv en m3∙s-1 est donné par : Dv=v∙S avec v en m∙s-1 et S en m2.
7. Indiquer la
condition sur la pression du liquide au niveau de l’aiguille pour que
le liquide contenu dans l’aiguille de la perfusion puisse pénétrer dans
la veine du patient.
La pression du liquide au niveau de l'aiguille doit être supérieure à la tension veineuse.
8. La tension veineuse du patient est de 8000 Pa. On rappelle que la tension veineuse correspond à la différence de pression Dp entre la pression du sang dans les veines et la pression atmosphérique : Δp = Psang - Patm.
Calculer la hauteur h à laquelle la poche de perfusion doit être placée.
8000 < ρliquide perfusé g h ; h > 8000 /(1080 x9,81) ; h > 0,76 m.
9. Une fois perfusé, le liquide contenant le produit de contraste se mêle au flux sanguin et se déplace à la vitesse vsang = 5 cm·s-1. Une veine a un diamètre moyen d = 0,5 cm.
9.1. Calculer la section S en m2 de la veine.
Donnée : 1cm2 = 1x10-4 m2.
S =3,14 x(0,5 /2)2 =0,196 cm2 = 1,96 10-5 m2 ~2 10-5 m2.
9.2. Calculer le débit volumique du sang et du liquide mêlés dans la veine.
Dv = S v =1,96 10-5 x5 10-2 =9,8 10-7 m3 s-1 =9,8 10-4L s-1 =0,98 mL s-1 ~1 mL s-1.
9.3.
Une des pathologies de ce patient fait que ses veines sont rétrécies.
Si le débit sanguin est inchangé, préciser en la justifiant la
variation de la vitesse v du sang
Le débit sanguin étant constant, si la section de la veine diminue, alors la vitesse du sang augmente.
|
...
|
|
Exercice 2. Contrôle qualité de la solution iodée (6 points)
Afin de compléter le premier diagnostic, monsieur X. se voit prescrire
une coronarographie. Cet examen utilise également du diiode, mais cette
fois-ci en tant que produit de contraste. Afin de s’assurer de la bonne
teneur en iode dans la solution injectée un technicien de laboratoire
va réaliser un titrage de la solution d’iode I2 par les ions thiosulfate S2O32-.
Le fabriquant qui fournit les hôpitaux assure que ses solutions de diiode sont dosées à 350 mg / mL.
Couples redox : I2 / I- ; I2 + 2e- = 2I-.
S4O62-/ S2O32-: S4O62-+ 2e- = 2S2O32-.
Concentration molaire de la solution contenant les ions thiosulfate : C2 = 2,0 mol·L-1.
Volume de la solution d’iode titrée : V1 = 10 mL
Masse molaire du diiode I2 : M = 246 g·mol-1.
1. Compléter le schéma suivant.
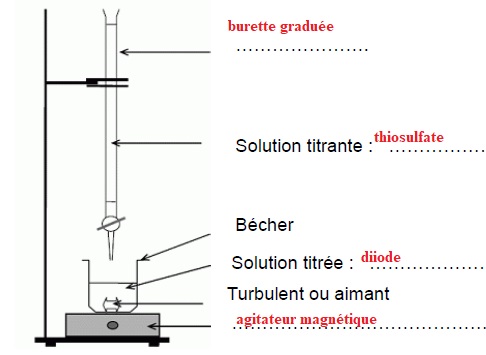
2. Donner la définition d’une espèce chimique oxydante et indiquer le réactif oxydant lors de cette réaction.
Un oxydant est une espèce chimique capable de gagner un ou plusieurs électrons. Le diiode joue le rôle d'oxydant.
3. Montrer que l’équation de la réaction de titrage est :
2S2O32- =S4O62-+ 2e- ;
I2 + 2e- = 2I-.
Ajouter et simplifier.
2S2O32- + I2 ---> S4O62-+ 2I-.
4. L’équivalence est observée pour un volume de solution titrante versé VE = 14,2 mL.
4.1. Donner la définition de l’équivalence d’un titrage.
A l'équivalence, les réactifs mis en présence sont en proportions stoecjiométriques.
4.2. Calculer la quantité de matière de thiosulfate versée à l’équivalence, notée nE.
nE =C2 VE =2,0 x14,2 =28,4 mmol.
4.3. Montrer que la relation entre les quantités de matière des espèces chimiques titrante et titrée à l’équivalence est : n(I2)=0,5 nE.
Une mole de diiode réagit avec 2 moles d'ions thiosulfate.
0,5 nE mole de diiode réagit avec nE moles d'ions thiosulfate.
5. En déduire la concentration molaire C de diiode I2 dans l’échantillon analysé.
n(I2)= 28,4 / 2 =14,2 mmol dans 10 mL.
14,2 / 10 = 1,42 mol / L.
6. Calculer la valeur de la concentration massique du diiode I2 dans l’échantillon analysé.
1,42 x M(I2) = 1,42 x 246 =349,32 ~349 g / L ou 349 mg / mL.
7. Indiquer si la concentration massique est en accord avec les données du fabriquant.
Les deux valeurs sont en accord, l'écart relatif étant inférieur à 1 %.
|
....
|
Exercice 3.
Conseils alimentaires. 6 points.
Au cours de l’examen médical monsieur X. est pesé, sa masse est de 86 kg.
Un extrait du bilan sanguin de monsieur X. indique les résultats suivants.
Analyses de Monsieur X
|
Valeurs de référence
|
Cholestérol HDL : 0,001 mol / L ( 1 mmol / L)
|
cholestérol HDL : > 0,90 mmol / L
|
| Cholestérol LDL : 0,004 mol / L ( 4 mmol / L) |
Cholestérol LDL : < 4,1 mmol / L. |
Triglycérides : 2,9 mmol /L
|
Triglycérides : < 1,7 mmol / L
|
Par ailleurs monsieur X. présente un taux de sucres trop élevé dans le sang. Un régime alimentaire lui est conseillé.
1. Interpréter l’extrait du bilan sanguin de monsieur X.
Le cholestérol est à peu près correct ; par contre le taux de triglycérides est trop élevé. Il en est de même pour les sucres.
2. Définir un triglycéride.
Un triglycéride est un triester du glycérol. ( glycérol + 3 acide gras).
3. Les triglycérides sont hydrolysés lors de la digestion. Compléter la réaction d’hydrolyse.
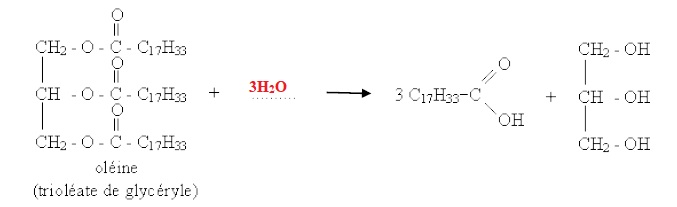
4. Le médecin
conseille à monsieur X de privilégier les graisses insaturées. L’huile
d’olive est riche en triglycéride dont l’hydrolyse conduit à de l’acide
oléique de formule C17H33COOH.
4.1. Justifier si cet acide gras est saturé ou insaturé.
Une chaine à 17 atomes de carbone est saturée si elle compte 17 x2 +1 = 35 atomes d'hydrogène.
Cet acide gras est insaturé.
4.2. L’huile d’olive peut-elle être conseillée dans le régime de monsieur X. ? Justifier.
Oui. Le médecin conseille à monsieur X de privilégier les graisses insaturées.
5. Pour
réduire sa consommation en sucres, monsieur X. remplace les boissons
sucrées par des boissons « light » qui contiennent de l’aspartame.
Entourer et nommer les groupes caractéristiques de la molécule
d’aspartame.
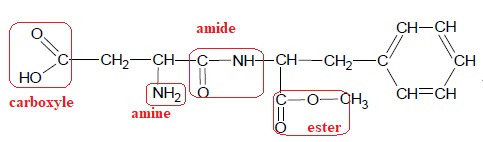
6. La Dose Journalière Admissible de l’aspartame est de 40 mg/kg. Définir la DJA.
C'est la masse maximale d'aspartame que l'on peut absorber par jour et par kg de masse corporelle sans risque pour la santé.
7. Calculer la quantité maximale d’aspartame que ce patient pourra consommer quotidiennement.
40 x 86 = 3440 mg ou 3,44 g.
8. Une canette de
soda de 33 cL apporte environ 40 mg d’aspartame. Monsieur X. a
l’habitude de boire au moins un café par jour dans lequel il ajoute
deux comprimés contenant chacun 18 mg d’aspartame. Calculer combien de
cafés et de canettes de soda monsieur X. peut consommer au maximum par
jour en respectant la DJA. Commenter ce résultat.
36 mg pour un café et 44 mg pour une canette soit 80 mg.
36 x5 = 180 mg pour 5 café et (3440-180) /40~81 canettes.
36 x10 = 360 mg pour 10 café et (3440-360) /40~77 canettes. Cela est peu probable.
|
|



