Mathématiques,
bac St2S Antilles septembre 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1.
6 points
L’animatrice
d’une maison de retraite propose deux sorties aux 80 résidents : la
visite d’une fromagerie et la visite d’un musée.
Sur les 80 résidents,
• 30 résidents se sont inscrits à la visite de la fromagerie,
• 25 résidents se sont inscrits à la visite du musée,
• 20 résidents se sont inscrits aux deux visites.
1. Compléter le tableau d’effectifs. Aucune justification n’est exigée.
|
Inscrits à la fromagerie
|
Non inscrits à la fromagerie
|
Total
|
Inscrits à la visite du musée
|
20
|
25-20=5
|
25
|
Non inscrits à la visite du musée
|
30-20=10
|
50-5=45
|
80-25=55
|
Total
|
30
|
80-30 = 50
|
80
|
2. On choisit un résident au hasard.
On note F l’évènement : « le résident est inscrit à la visite de la fromagerie ».
On note M l’évènement : « le résident est inscrit à la visite du musée ».
a. Déterminer les probabilités P(F) et P(M).
P(F) = 30 / 80 =0,375.
P(M) =25 / 80 =0,3125.
b. Définir par une phrase l’évènement F ∩M et calculer la probabilité de cet évènement.
Probabilité q'un résident se soit inscrit aux deux visites : 20 /80 = 0,25.
c. Calculer la probabilité que le résident choisi au hasard soit inscrit à la visite de la fromagerie ou à la visite du musée.
P(F u M) =P(F) + P(M) -P(F n M) =0,375 +0,3125 -0,25 =0,4375.
3. Déterminer PF (M). Interpréter le résultat dans le contexte de l’exercice.
PF (M) =P(F n M) / P(M) =0,25 / 0,3125 =0,80.
Probabilité qu'un résident visite le musée sachant qu'il a visité la fromagerie.
4. a.
Montrer que si un résident n’est pas inscrit à la visite du musée,
alors il y a plus de 8 chances sur 10 pour qu’il ne soit pas inscrit à
la visite de la fromagerie.
Pnon M( non F) =45 / 50 =0,90.
b.
L’animatrice affirme que si un résident n’est pas inscrit à une des
visites, il y a une forte probabilité qu’il ne soit pas inscrit à
l’autre.
Cette affirmation est-elle correcte ? Justifier la réponse.
Pnon F( non M) =10 / 45 ~0,222.
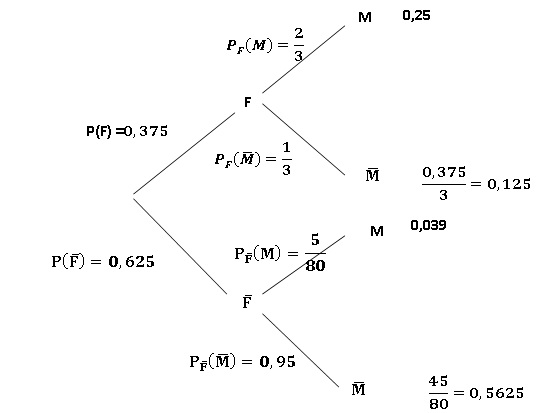
L'affirmation est vraie.
|
...
|
|
Exercice 2. 8 points.
En France, nous sommes tous des donneurs potentiels d’organes et de tissus, sauf en cas de refus explicite.
Dans un rapport sur l’application de la loi de bioéthique, en date de
janvier 2018, l’agence de biomédecine fait état de l’évolution du
nombre de donneurs décédés en état de mort encéphalique, et des
prélèvements effectifs sur ces donneurs.
Les parties A et B de cet exercice peuvent être traitées de manière indépendante.
Partie A : donneurs décédés
Le nombre de donneurs décédés, en état de mort encéphalique, de 2012 à 2016, est donné par le tableau suivant :
Année
|
2012
|
2013
|
2014
|
2015
|
2016
|
Rang
de l'année xi
|
0
|
1
|
2
|
3
|
4
|
Nombre
de donneurs yi
|
3301
|
3336
|
3547
|
3579
|
3676
|
1. Représenter le nuage de points de coordonnées (xi ; yi ) associé aux données du tableau précédent.
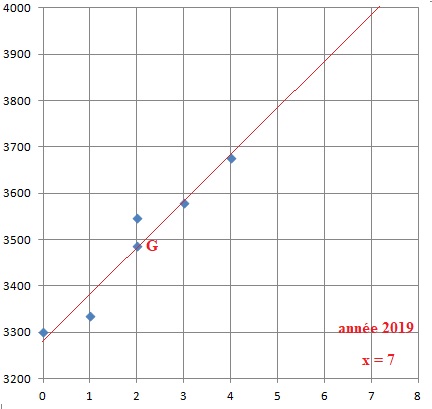
2. a. Montrer que les coordonnées du point moyen G de ce nuage sont G(2; 3487,8).
(0 +1 +2 +3 +4 ) 5 =2.
(3301 +3336 +3547 +3579 +3676) / 5 = 3487,8.
b. Placer G sur le graphique.
3. Soit (D) la droite d’équation = 99,1x +3289,6.
a. Montrer que G appartient à cette droite (D).
99,1 x2 +3289,6 =3487,8 = yG.
b. Tracer la droite (D) en précisant les coordonnées des points utilisés.
Point G et point de coordonnées (0 ; 3289,6).
4. On décide de
faire un ajustement affine du nuage de points par la droite (D). On
considère que cet ajustement est valable jusqu’en 2025. À l’aide de cet
ajustement, estimer :
a. graphiquement, l’année à partir de laquelle le nombre de donneurs dépassera 4 000 ;
b. par le calcul, le nombre de donneurs en 2023.
x = 11 ; y = 99,1 x11 +3289,6 ~4380.
PARTIE B :
Les donneurs décédés, en état demort encéphalique, effectivement prélevés sont donnés par le tableau suivant :
Année
|
2012
|
2013
|
2014
|
2015
|
2016
|
Nombre de donneurs prélevés
|
1589
|
1627
|
1655
|
1769
|
1770
|
La tendance de croissance observée sur la période 2012-2016 permet de
modéliser l’évolution du nombre de donneurs prélevés chaque année, par
une augmentation annuelle de 2,7% à partir de l’année 2016.
On note alors vn l’estimation, selon ce modèle, du nombre de donneurs prélevés au cours de l’année (2016+n), pour n entier naturel.
Ainsi v0 = 1770.
1. Calculer v1 et v2 (arrondir les résultats à l’unité). Interpréter le résultat trouvé pour v2 dans le contexte de l’exercice.
v1 = 1,027 v0 = 1,027 x1770 ~1818.
v2 = 1,027 v1 = 1,027 x1818 ~1867.
2. On utilise la feuille de calcul ci-dessous pour calculer l’estimation selon ce modèle du nombre de donneurs prélevés.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
Année
|
2016
|
2017
|
2018
|
2019
|
2020
|
2021
|
2022
|
2023
|
2
|
Nombre de donneurs prélevés
|
1770
|
|
|
|
|
|
|
|
Quelle formule, à recopier vers la droite, peut-on saisir dans la
cellule C2 pour obtenir l’estimation du nombre de donneurs prélevés les
années suivantes ?
=B2*1,027
3. Indiquer, sans justification, la nature de la suite (vn) et préciser sa raison.
Suite géométrique de raison 1,027.
4. Pour tout entier naturel n, exprimer vn en fonction de n.
vn = 1770 x1,027n.
5. Montrer que, selon ce modèle, on peut estimer à 2 133 le nombre de donneurs prélevés en 2023.
n =7 ; v7 = 1770 x1,0277 ~2133.
Partie C :
Un analyste affirme que, selon les estimations des parties A et B, la
proportion de donneurs décédés en état de mort encéphalique en 2023 qui
seront effectivement prélevés ne dépassera pas 50%. Cette affirmation
est-elle correcte ? Justifier la réponse.
2133 /4380 x100 =48,7 %. L'affirmation est correcte.
|
....
|
Exercice 3. 6 points.
Le
réseau Sentinelles a recensé en continu le nombre de personnes
atteintes de la grippe sur une période de 15 semaines au cours de
l’hiver 2017.
Le seuil épidémique étant fixé à 175 cas pour 100 000 habitants, le
suivi épidémiologique est déclenché après 7 semaines de recensement et
s’achève à la fin de la 15e semaine.
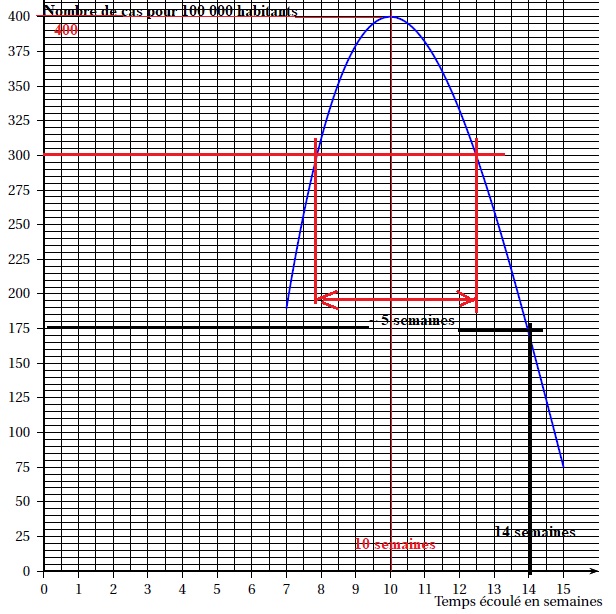
La courbe suivante représente l’évolution du nombre de cas pour 100 000 habitants sur la période de suivi épidémiologique.
Partie A : Lectures graphiques
On fera apparaÎtre les traits utiles à la lecture.
1. a. Après combien de semaines de recensement, le pic épidémiologique a-il été atteint ?
10 semaines
b. Quel a été le nombre de cas recensés pour 100 000 habitants au moment de ce pic ?
400
2. Durant combien de semaines, le nombre de cas de grippe pour 100 000 habitants a-t-il été supérieur à 300?
environ 5 semaines.
3. Après combien de
semaines de recensement le nombre de cas de grippe pour 100 000
habitants est-il redevenu inférieur au seuil épidémique ?
14 semaines.
Partie B : Étude de fonction
Soit la fonction f définie sur l’intervalle [7; 15] par :
f (x) = 1,3x3 −58,5x2 +780x −2850.
Cette fonction f permet de modéliser, en fonction du temps x exprimé en
semaines, l’évolution du nombre de cas de grippe pour 100 000 habitants
sur la période de suivi épidémiologique.
1. Calculer f (7), f (10) et f (15).
f(7) = 1,3 x73 -58,5 x72 +780 x7 -2850 =445,9- 2866,5 +5460 -2850 =189,4.
f(10) = 1,3 x103 -58,5 x102 +780 x10 -2850 =1300- 5850 +7800 -2850 =400.
f(15) = 1,3 x153 -58,5 x152 +780 x15 -2850 =4387,5- 13162,5 +11700 -2850 =75.
2. On note f ′ la fonction dérivée de la fonction f .
a. Déterminer f ′(x) pour tout réel x de l’intervalle [7; 15].
f 'x) =1,3 x3 x2 -2 x58,5 x +780 =3,9 x2 -117 x +780
b. Vérifier que f ′(x) = 3,9(x −10)(x −20).
On développe : 3,9 x2 -39 x -78 x +780 = 3,9 x2 -117 x +780.
3. Compléter le tableau, qui donne le signe de la dérivée f ′ et les variations de f .
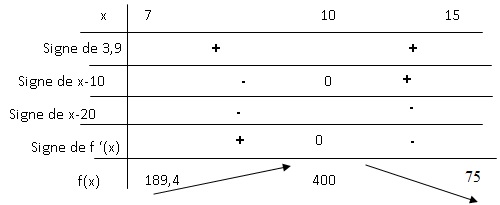
|
|