Mathématiques,
bac St2s Nlle Calédonie 03 / 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Exercice 1. ( 5 points)
Cet exercice est un questionnaire à choix multiples (QCM).
Pour chaque question, quatre réponses sont proposées parmi lesquelles une seule est correcte.
Indiquer sur la copie le numéro de la question suivi de la réponse choisie. Aucune justification n’est demandée.
Chaque bonne réponse rapporte un point. Aucun point n’est enlevé pour une absence de réponse ou pour une réponse inexacte.
L’évolution des dépenses annuelles de protection sociale par habitant
en France est donnée par le tableau ci-dessous, extrait d’une feuille
de calcul. (Source : Eurostat).
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
1
|
Année
|
2011
|
2012
|
2013
|
2014
|
2015
|
2016
|
2017
|
2
|
Dépenses par habitant (€)
|
10182
|
10402
|
10539
|
10721
|
|
|
|
3
|
Pourcentage d'évolution entre deux années consécutives
|
|
|
|
|
|
|
|
1. Le pourcentage d’augmentation du montant des dépenses par habitant entre les années 2011 et 2012, arrondi à 0,01%, est :
a. 2,16% ; b. 0,0216% ; c. 1,021% ; d. −2,11%.
(10402 -10182) / 10182 x100 =2,16 %
À partir de l’année 2014, on admet que les dépenses de protection sociale par habitant augmentent de 1,7% par an.
2. La formule à
saisir dans la cellule F2, qui recopiée vers la droite, permettra
d’afficher les valeurs en euro du montant des dépenses de protection
sociale par habitant pendant les années qui suivent 2014 est :
a. = E2 * 0,017 ; b. 10 721 * 1,017 ; c. $E$2 * 1,017 ; d. = E2 * 1,017 .
3. Dans le tableau,
les cellules C3 à H3 sont au format pourcentage. Une formule à saisir
dans la cellule C3 qui, recopiée vers la droite, permet d’afficher le
pourcentage d’évolution du montant des dépenses de protection sociale
par habitant entre deux années consécutives est :
a. = C2/B2 ; b. =C2−B2/B2 ; c. =(C2−B2)/B2 ; d. =(C2−$B2)/$B2.
4. On désigne par n un entier naturel. On note un le montant des dépenses par habitant pour l’année (2014+n) ; ainsi u0 = 10721. Le montant des dépenses de protection sociale par habitant pour l’année 2018 est :
a. 10721×1,0174 euros ; b. 10721×1,0175 euros
c. 10721×0,0174 euros ; d. 10721×0,0175 euros
5. L’année à partir de laquelle le montant des dépenses de protection sociale par habitant aura dépassé 12 000 euros est :
a. 2020 ; b. 2021 ; c. 2022 ; d. 2016 .
10721 x 1,017n > 12000 ; 1,017n > 12000 / 10721 ; 1,017n > 1,119 ;
n log (1,017) > log 1,119 ; n > 6,68 soit 7.
Année 2014 +7 = 2021.
|
|
|
Exercice 2. 6 points.
Une étude portant sur l’évolution du nombre de médecins exerçant en
Espagne a été effectuée durant 11 ans. Elle a permis d’établir le
tableau suivant qui donne le nombre moyen de médecins pour 100 000
habitants, de 2005 à 2015.
Année
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
2014
|
2015
|
Rang de l'année xi
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Nombre de médecins
pour 100 000 habitants yi
|
458
|
460
|
463
|
469
|
477
|
485
|
490
|
489
|
499
|
512
|
522
|
1. a. Représenter le nuage de points de coordonnées (xi ; yi ) dans un repère orthogonal.
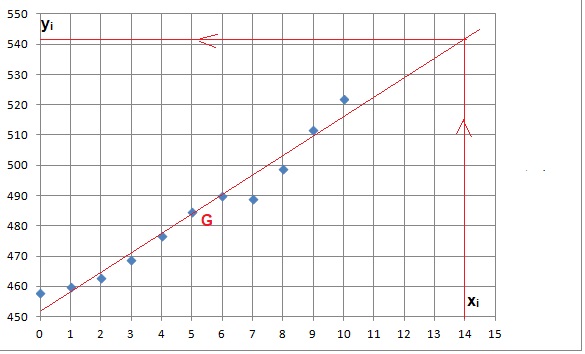
b. Déterminer les coordonnées du point moyen G de ce nuage de points et le placer dans le repère précédent.
xG = 5 ; yG = 484.
2. Pour estimer le
nombre de médecins en Espagne dans les années futures, on utilise un
ajustement affine de ce nuage de points. On admet que la droite D
d’équation y = 6,3x + 452,5 réalise un tel ajustement, valable jusqu’en
2025.
a. Donner les coordonnées de deux points de la droite D puis la tracer dans le repère précédent.
La droite passe par le point G et le point de coordonnée ( 0 ; 452,5).
b. Déterminer graphiquement le nombre de médecins pour 100 000 habitants en 2019 selon cette estimation.
En 2019, x = 14 , donc 541 médecins pour 100 000 habitants.
3. Lorsque le
pourcentage de médecins dans une population est supérieur à 0,55%, on
dit que cette population est suffisamment pourvue. Dans les questions
suivantes, les résultats seront arrondis à l’unité.
a. Calculer le nombre minimum de médecins pour qu’une population de 100 000 habitants soit suffisamment pourvue.
100 000 x0,55 / 100 = 550.
b. En utilisant
l’ajustement affine précédent, déterminer à partir de quelle année la
population espagnole sera suffisamment pourvue en médecins ; justifier
la réponse en précisant la méthode utilisée.
550 = 6,3 x +452,5 ; 6,3 x = 550 -452,5 =97,5 ; x = 97,5 / 6,3 ; x 15,47 ; x = 16 ; année 2021.
|
|
|
|
Exercice 3. 9 points
Partie A.
Une entreprise fabrique des emballages en carton spécifiques aux médicaments.
La production quotidienne sur une de ses lignes de production, exprimée en millier d’emballages, varie entre 5 et 20.
Le coût correspondant à la fabrication de x milliers d’emballages,
exprimé en euro, est modélisé par la fonction f définie sur
l’intervalle [5; 20] par :
f (x) = x3 −24x2 +180x +250.
1. On note f ′ la fonction dérivée de la fonction f sur l’intervalle [5; 20].
a. Calculer f ′(x).
f '(x) = 3x2 -48x+180.
b. Démontrer que, pour tout nombre réel x de l’intervalle [5; 20], on a : f ′(x) = 3(x −10)(x −6).
f '(x) = 3 (x2 -8x +60).
On développe : (x-10)(x-6) = x2-6x-10x+60 = x2 -8x +60
2. a. Étudier le signe de f ′(x) pour tout x de l’intervalle [5; 20].
b. Construire le tableau de variation de la fonction f sur l’intervalle [5; 20].
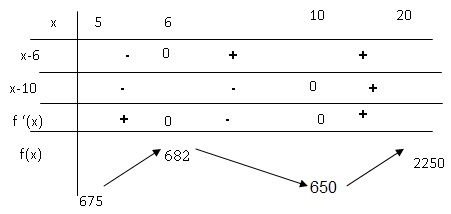
c. Quel est le nombre d’emballages à fabriquer pour obtenir le coût minimal ? Quel est alors ce coût minimal ?
10 000 emballages ; coût minimum 650 € pour 1000 emballages.
Partie B.
Chaque année depuis 1995, un institut de sondage mène une étude auprès
du grand public sur les comportements en matière du tri des Médicaments
Non Utilisés (M.N.U.). L’étude est effectuée sur un panel de 1 000
personnes représentatif de la population française
âgée de 18 ans et plus.
L’enquête de 2017 montre que 79% des Français déclarent déposer leurs Médicaments Non Utilisés (M.N.U.) chez le pharmacien.
Parmi ceux qui n’ont pas déposé leurs M.N.U. en pharmacie en 2017, 87% se déclarent prêts à le faire en 2018.
Parmi ceux qui le faisaient déjà, 99% déclarent qu’ils continueront à le faire en 2018.
On choisit au hasard une personne du panel. Chaque personne a la même probabilité d’être choisie.
Pour tout évènement E, on note non E l’évènement contraire de E.
On considère les évènements suivants :
• D : « la personne déclare avoir déposé en 2017 ses M.N.U. en pharmacie » ;
• F : « la personne déclare qu’elle déposera ses M.N.U. en pharmacie en 2018 ».
1. Reproduire et compléter l’arbre de probabilité ci-dessous qui représente la situation.
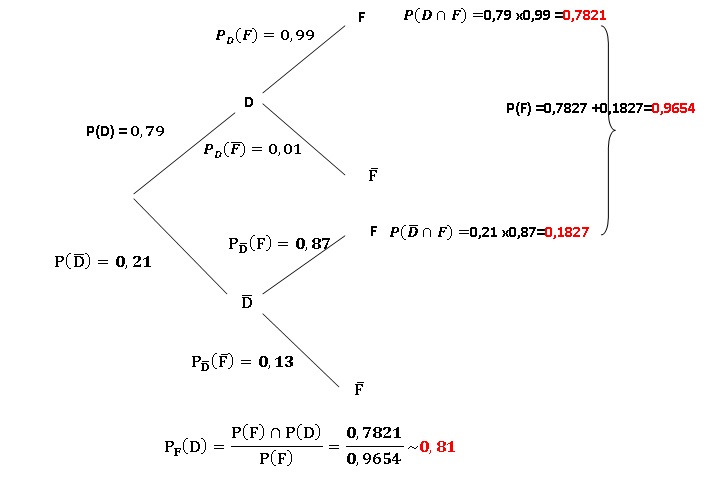
2. a. Calculer la
probabilité que la personne choisie déclare avoir déposé ses M.N.U. en
pharmacie en 2017 et prévoit de les déposer en 2018.
b. Montrer que la probabilité de l’évènement non D ∩F est égale à 0,1827.
c. En déduire la probabilité de l’évènement F.
3. Sachant que la
personne choisie déclare qu’elle déposera ses médicaments en 2018,
calculer la probabilité qu’elle les ait déjà déposés en 2017. Arrondir
le résultat au centième.
|
|
|