Mathématiques,
bac S Polynésie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
..
|
|
Exercice 1 : Commun à tous les
candidats (5 points).
Les probabilités seront arrondies à 0,01.
Un commerçant vient de s'équiper d'un distributeur de glace.1.
La durée, en mois, de fonctionnement sans panne de son distributeur de
glaces à l’italienne est modélisée par une variable aléatoire X qui
suit une loi exponentielle de paramètre l¸ où l ¸
est un réel strictement positif (on rappelle que la fonction f de
densité de la loi exponentielle est donnée sur [0 ; +∞[ par f (x) = le−lx.
Le vendeur de l’appareil assure que la durée moyenne de fonctionnement
sans panne de ce type de distributeur, c’est-à-dire l’espérance
mathématique de X, est de 10 mois.
a. Justifier que l= 0,1.
l = 1 / E = 1 /10 = 0,1 mois-1.
b. Calculer la probabilité que le distributeur de glaces à l’italienne n’ait connu aucune panne pendant les six premiers mois.
P(X > 6) = e-0,6=0,55.
c.
Sachant que le distributeur n’a connu aucune panne pendant les six
premiers mois, quelle est la probabilité qu’il n’en connaisse aucune
jusqu’à la fmde la première année ? Justifier.
La loi exponentielle est sans mémoire.
PX >6(X >12) =P(X >6) = 0,55.
d.
Le commerçant remplacera son distributeur de glaces à l’italienne au
bout d’un temps t , exprimé en mois, qui vérifie que la probabilité de
l’évènement (X > t ) est égale à 0,05. Déterminer la valeur de t
arrondie à l’entier.
P(X > t) = 0,05 =e-lt ; -lt = ln (0,05) ; t = - ln(0,05 ) 0,1 =29,96.
t ~ 30 mois.
2.
La notice du distributeur de glaces précise que le distributeur fournit
des glaces à l’italienne dont la masse est comprise entre 55 g et 65 g.
On considère la variable aléatoire M représentant la masse, en grammes,
d’une glace distribuée.
On admet que M suit la loi normale d’espérance 60 et d’écart-type 2,5.
a. Calculer
la probabilité que la masse d’une glace à l’italienne choisie au hasard
parmi celles distribuées soit comprise entre 55 g et 65 g.
P(X < 55) =0,02275 ; P(X < 65) =0,9773 :
P( 55 < X < 65) = 0,9773 -0,02275 ~0,95.
b.
Déterminer la plus grande valeur de m, arrondie au gramme près, telle
que la probabilité P(M > m) soit supérieure ou égale à 0,99.
P(M > 54) = 0,9918 ; P(M > 55) = 0,9772 ; m = 54.
3.
Le distributeur de glaces à l’italienne permet de choisir un seul des
deux parfums : vanille ou fraise. Pour mieux gérer ses achats de
matières premières, le commerçant fait l’hypothèse qu’il y aura en
proportion deux acheteurs de glace à la vanille pour un acheteur de
glace à la fraise.
Le premier jour d’utilisation de son distributeur, il constate que sur
120 consommateurs, 65 ont choisi de la glace à la vanille.
Pour quelle raison mathématique pourrait-il mettre en doute son hypothèse ? Justifier.
n = 120 ; p = 2 / 3 ;
n > 30 ; np = 120 x 2 /3 = 80 > 5 ; n(1-p) = 120 / 3 = 40 > 5.
Les conditions sont réunies pour définir un intervalle de fluctuation asymptotique au seuil de 95 %.
1,96 (p(1-p) / n)½ =1,96 (2 / (9 x120))½ =0,0843.
Intervalle de fluctuation :[0,667 -0,0843 ; 0,667 +0,0843] soit : [0,58 ; 0,76 ].
La fréquence observée est égale à 65 / 120 = 0,54. Elle n'appartient pas à cet intervalle.
Au risque d'erreur de 5 %, l'hypothèse du commerçant est fausse.
|
|
|
Exercice
2 : Commun à tous les candidats (5 points)
L’écoulement de l’eau d’un robinet a un débit constant et modéré.
On s’intéresse en particulier à une partie du profil d’écoulement
représentée en annexe 1 par la courbe C dans un repère orthonormé.
Partie A.
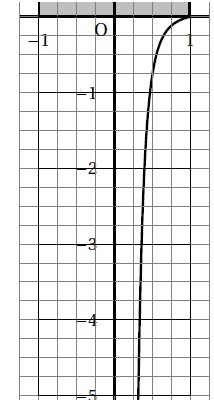
On considère que la courbe C donnée en annexe 1 est la représentation
graphique d’une fonction f dérivable sur l’intervalle ]0; 1] qui
respecte les trois conditions suivantes :
(H) : f (1) = 0 ; f ′(1) = 0,25 et la limite en O+ de f(x) est égale à moins l'infini.
1. La fonction f peut-elle être une fonction polynôme du second degré ? Pourquoi ?
f(x) = ax2 +bx +c ; a, b, c réels et a différents de zéro.
La limite de f en 0+ est égale à c et non pas à moins l'infini.
2. Soit g la fonction définie sur l’intervalle ]0; 1] par g (x) = k lnx.
a. Déterminer le réel k pour que la fonction g respecte les trois conditions (H).
g(1) = k ln(1) =0 ; la première condition est vérifiée.
g'(x) = k /x ; g'(1) = k = 0,25.
g(x) = 0,25 ln(x).
La limite en O+ de ln(x) est égale à moins l'infini : condition 3 respectée.
b. La courbe représentative de la fonction g coïncide-t-elle avec la courbe C ? Pourquoi ?
g(0,5) = 0,25 ln (0,5) ~0,173 ;
f(0,5) ~ -0,7 ( lecture courbe).
Les courbes ne coïncident pas.
3. Soit h la fonction définie sur l’intervalle ]0; 1] par h(x) = a /x4 +bx où a et b sont des réels.
Déterminer a et b pour que la fonction h respecte les trois conditions (H).
h(1) = a +b = 0 ; a = -b.
h'(x) = -4a / x5 +b ; h'(1) = 0,25 =-4a +b ; 5b = 0,25 ; b = 1 /20 =0,05 ; a = -0,05.
h(x) = 0,05( -1 /x4 +x).
Partie B.
On
admet dans cette partie que la courbe C est la représentation graphique
d’une fonction f continue, strictement croissante, définie et dérivable
sur l’intervalle ]0; 1] d’expression :
f (x) = 0,05 (x-1 /x4).
1. Justifier que l’équation f (x) = −5 admet sur l’intervalle ]0; 1] une unique solution qui seranotée a. Déterminer une valeur approchée de a à 10−2 près.
f '(x) = 0,05 (1+4 /x5) est positive sur ]0; 1] ; f(x) estcontinue et strictement croissante sur cet intervalle.
De plus f(1) = 0 et la limite de f(x) en 0+ est moins l'infini.
D'après le corollaire du théorème des valeurs intermédiaires, f(x) =-5 admet une solution unique sur ]0; 1].
f(-0,31) = -5,399 ; f(-0,32) = -4,752 ; a ~0,31.
2. On admet que le volume d’eau en cm3, contenu dans les 5 premiers centimètres de l’écoulement, est donné par la formule :
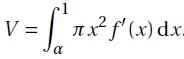
a. Soit u la fonction dérivable sur ]0; 1] définie par u(x) =1/(2x2). Déterminer sa fonction dérivée.
u'(x) = -1 / x3.
b. Déterminer la valeur exacte de V . En utilisant la valeur approchée de a obtenue à la question 1, donner alors une valeur approchée de V .
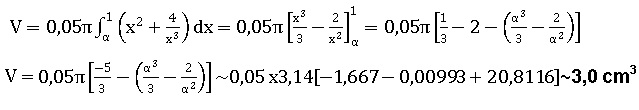
|
|
|
|
Exercice 3 : Commun à tous les
candidats (5 points)
On considère la suite (In) définie par 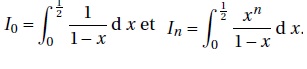
1. Montrer que I0 = ln(2).
Une primitive de 1 / (1-x) est -ln(1-x) ; I0 =- [ln(1-0,5) -ln(1)] = -ln(0,5) = ln(2).
2. a. Calculer I0 −I1.
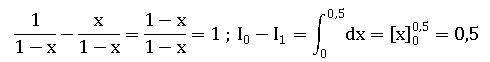
b. En déduire I1.
I1 =ln(2)- 0,5.
3. a. Montrer que, pour tout entier naturel n, In −In+1 =0,5n+1 / (n+1).
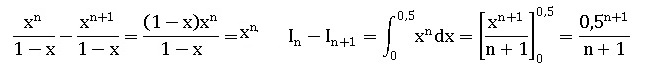 . .
b. Proposer un algorithme permettant de déterminer, pour un entier naturel n donné, la valeur de In.
Variables
I, réel ; a, n entier
I = ln(2)
Pour a allant de 1 à n
I =I- 0,5a / a
Fin pour.
4. Soit n un entier naturel non nul.
On admet que si x appartient à l’intervalle [0 ; 0,5] alors 0 < xn / (1-x) < 1 / 2n-1.
a. Montrer que pour tout entier naturel n non nul, 0 < In < 1 / 2n.
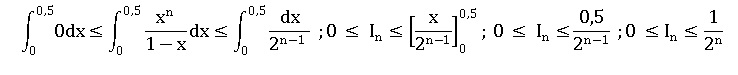
b. En déduire la limite de la suite (In) lorsque n tend vers +∞.
1 / 2n tend vers zéro si n tend vers plus l'infini.
D'après le théorème d'encadrement, In tend vers zéro si n tend vers plus l'infini.
5. Pour tout entier naturel n non nul, on pose
Sn =0,5 +0,52 /2 +0,53 / 3 +.... +0,5n / n.
a. Montrer que pour tout entier naturel n non nul, Sn = I0 - In.
Sn = 0,5 +0,52 /2 +0,53 / 3 +.... +0,5n / n.
I0 −I1 =0,5 ; I1 −I2 =0,52 / 3 ; I2 −I3 =0,53 / 4 ; In-1 −In =0,5n / n.
Sn =I0 −I1 + I1 −I2 +I2 −I3 +..... + In-1 −In =I0 - In.
b. Déterminer la limite de Sn lorsque n tend vers +oo.
In tend vers zéro si n tend vers plus l'infini.
Sn tend vers I0 = ln(2) si n tend vers plus l'infini.
|
|
Exercice 4 5 points
Pour les candidats n’ayant pas suivi la spécialité
Sur la figure donnée en annexe 2 à rendre avec la copie :
• ABCDEFGH est un parallélépipède rectangle tel que AB = 12, AD = 18 et AE = 6
• EBDG est un tétraèdre..
L’espace est rapporté à un repère orthonormal d’origine A dans lequel
les points B, D et E ont pour coordonnées respectives B(12; 0; 0), D(0;
18; 0) et E(0; 0; 6).
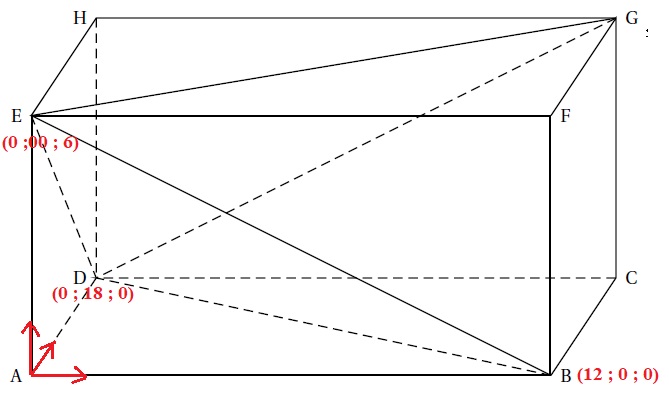
1. Démontrer que le plan (EBD) a pour équation cartésienne 3x +2y +6z −36 = 0.
Equation cartésienne d'un plan : ax +by +cz +d=0.
E (0 ; 0 ; 6) appartient à ce plan : 6c +d = 0 ; c = -d /6.
B (12 ; 0 ; 0) appartient à ce plan : 12a +d = 0 ; a = -d / 12
D (0 ; 18 ; 0) appartient à ce plan : 18b +d = 0 ; b = -d /18.
-d x /12 -d y /18 -d z /6 +d =0 ;
en multipliant par -36 et en simplifiant par d : 3x+2y+6z -36 =0.
2. a. Déterminer une représentation paramétrique de la droite (AG).
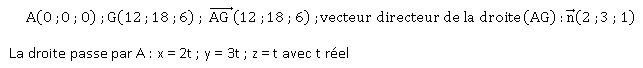
b. En déduire que la droite (AG) coupe le plan (EBD) en un point K de coordonnées (4; 6; 2) .
K appartient à la droite : 4 = 2t ; t = 2 ; y = 6 ; z = 2.
Si K appartient au plan, les coordonnées de K vérifient l'équation cartésienne du plan (EBD).
3 x4 +2 x6 +6 x2 -36 = 0 est vérifié. Donc K appartient à ce plan.
3. La droite (AG) est-elle orthogonale au plan (EBD) ? Justifier.
Coordonnées d'un vecteur perpendiculaire au plan (EBD): ( 3 ; 2 ; 6)
Coordonnées du vecteur directeur de la droite (AG) : (2 ; 3 ; 1 )
Ces deux vecteurs n'étant pas colinéaires, la droite (AG) n'est pas parpendiculaire au plan( EBD).
4. a. Soit M le milieu du segment [ED]. Démontrer que les points B, K et M sont alignés.
M((xE +xD) / 2 ; (yE +yD) / 2 ; (zE +zD) / 2 ;) soit M(0 ; 9 ; 3).

b. Construire alors le point K sur la figure donnée en annexe 2 à rendre avec la copie.
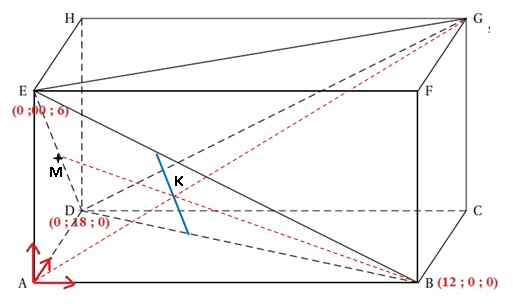
On note P le plan parallèle au plan (ADE) passant par le point K.
a. Démontrer que le plan P coupe le plan (EBD) selon une parallèle à la droite (ED).
b. Construire alors sur l’annexe 2 à rendre avec la copie l’intersection du plan P et de la face EBD du tétraèdre EBDG.
Les plans (AED) et (EBD) se coupent suivant la droite (ED).
Le plan P est parallèle au plan (AED) et de plus il passe par le point K.
Par suite K appartient aux plans P et (EBD).Les plans P et (EBD) se coupent selon une droite parallèle à (ED).
|
|
|