Accorder
un diapason,
bac S M�tropole 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
.
.
|
|
Un
groupe de quatre �l�ves dispose
de quatre diapasons en aluminium ayant des branches de m�me largeur d =
7 mm et de longueurs L diff�rentes. En modifiant la largeur des
branches ou leur longueur, il est possible d’ajuster la fr�quence du
son �mis par le
diapason.
Le but de cet exercice est de comprendre comment on peut modifier ces
quatre diapasons afin qu’ils �mettent tous un son de fr�quence f = 440 Hz,
c'est-�-dire un La3.
Chaque �l�ve a enregistr� le son �mis par les quatre diapasons
(num�rot�s de 1 � 4) � l’aide d’un microphone reli� � un ordinateur. Le signal obtenu a
permis de d�terminer
la fr�quence du son �mis par chacun des diapasons.
Le tableau 1 ci-dessous regroupe les r�sultats obtenus et fait le lien
entre la fr�quence f du son �mis et la longueur L des branches du diapason.
Num�ro du diapason
|
1
|
2
|
3
|
|
Fr�quence du son �mis ( Hz)
|
485
|
384
|
320
|
256
|
Longueur des branches (m)
|
0,108
|
0,121
|
0,133
|
0,147
|
1/L2 ( m-2)
|
85,7
|
68,3
|
56,5
|
46,3
|
(1/L2 ) / f
|
0,177
|
0,179
|
0,177
|
0,181
|
En
utilisant un mod�le th�orique, on peut �tablir qu’un diapason en
aluminium dont les branches ont une largeur d et une longueur L �met un
son de fr�quence f telle que :
f = 0,16 [EA / rA]� d / L2 (1).
o� : - EA (en kg�m-1�s-2) est une constante caract�ristique de l’aluminium ;
- ρA (en kg�m-3) est la masse volumique de l’aluminium ;
- f, d et L sont exprim�es dans les unit�s de base du Syst�me International.
Lorsqu’il est tenu � la main, le son produit par le diapason est
difficilement audible. Pour le rendre pur et l’amplifier, Albert
Marloye eut l’id�e, en 1839, de poser la base du diapason sur une
caisse de r�sonance. Il s’agit d’une bo�te en bois ouverte � l’une de
ses extr�mit�s. Dans le cadre d’un mod�le simplifi�, une onde sonore
sinuso�dale de longueur d’onde λ est amplifi�e par la caisse �
condition que la profondeur D de la cavit� interne soit un multiple
entier impair de λ/4 (exemples : λ/4 ; 3λ/4 ;
5λ/4 ; …).
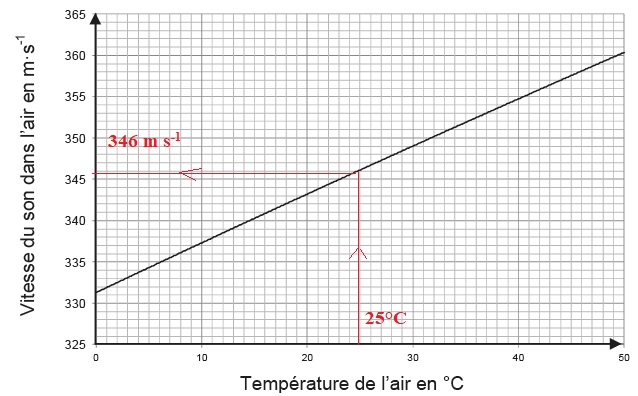
La vitesse du son dans l’air d�pend de la temp�rature selon la courbe ci-dessous.
|
|
........
|
|
Questions pr�liminaires.
1. Montrer, par une
analyse dimensionnelle, que la formule (1) est homog�ne et qu’elle est
compatible avec les mesures du tableau 1.
EA / rA s'exprime en m2 s-2 ; [EA / rA]� s'exprime en m s-1 ;
d / L2 s'exprime en m-1 ; [EA / rA]� d / L2 s'exprime en s-1 ;
de plus une fr�quence s'exprime en s-1.
0,16 [EA / rA]� est constant dans cette �tude.
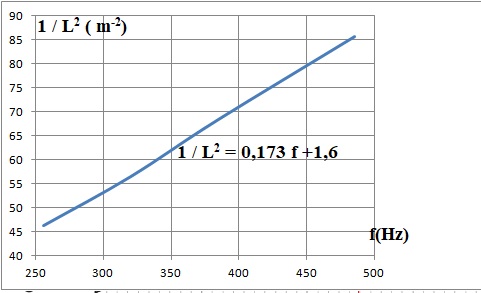
f est donc proportionnel � d /L2 ( mais aussi � 1 /L2, d �tant constant) ainsi que le confirme le graphe suivant :
2. D�terminer la longueur d’onde d’un son de fr�quence 440 Hz se propageant dans l’air � 25 �C.
l = v / f =346 / 440 ~ 0,786 m = 78,6 cm.
Probl�me.
Dans un atelier disposant d’outils de pr�cision, on peut couper les
branches d’un diapason en aluminium � la longueur L d�sir�e ou diminuer
la largeur d des branches. On peut �galement y fabriquer des caisses de
r�sonance en bois.
On dispose des quatre diapasons num�rot�s de 1 � 4. Indiquer la ou les
instruction(s) � donner � l’atelier pour que chacun des quatre
diapasons �mette un son de fr�quence f = 440 Hz (La3) amplifi� de fa�on
optimale par une caisse de r�sonance en bois. Le dispositif sera
utilis� dans une salle � 25�C.
La
profondeur D de la cavit� interne soit un multiple entier impair de λ/4
(exemples : λ/4 =19,6 cm ; 3λ/4 =59 cm, trop encombrant )
Diapason 1 : 1 /L2 = 0,173 x440 +1,6 = 77,72 ; L = 0,113 m =11,3 cm. Impossible de rallonger les branches.
Il faut diminuer la largeur d :
1 /L2 = 0,173 f +1,6 ; on multiplie chaque membre par d = 7 10-3.
d /L2 = 7 10-3 / L2 = 2,211 10-3 f +1,12 10-2.
d' /L2 = 1,211 10-3 x 440 +1,12 10-2 =0,544 ;
d' = 0,544 x 0,1082 =6,35 10-3 m = 6,35 mm.
Diapason 2 : on racourcit les branches de 12,1-11,3 =0,8 cm. La largeur reste inchang�e.
Diapason 3 : on racourcit les branches de 13,3-11,3 =2 cm. La largeur reste inchang�e.
Diapason 4 : on racourcit les branches de 14,7-11,3 =3,4 cm. La largeur reste inchang�e.
|
|
|
