On vous donne le la, bac S Métropole 2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Un diapason à fourche est constitué d’une pièce métallique en forme de U, à la base de laquelle est fixée une tige qui sert à le tenir à la main ou à le fixer à un support. Lorsqu’on frappe le diapason, il « sonne ». Cet objet a été inventé au début du XVIIIème siècle par le luthiste anglais John Shore. Il servait alors à accorder tous les instruments d’un orchestre entre eux afin qu’ils jouent « juste ». La note de référence utilisée étaitsouvent le « La3 » soit un son de fréquence 440 Hz. 1. Caractéristiques du son produit par le diapason. On enregistre à l’aide d’un microphone relié à un dispositif d’enregistrement le signal sonore émis par un diapason, tenu à la main (sans caisse de résonance). On obtient le signal suivant. 1.1. Dans ces conditions d’utilisation du diapason, le son obtenu est-il pur ? Justifier. La courbe n'étant pas uns sinusoïde, le son n'est pas pur, il est complexe. 1.2. Le constructeur annonce que le diapason étudié est en acier et qu’il émet un La3, soit un son de fréquence 440 Hz. En exploitant au mieux l’enregistrement de la figure 1, estimer la période de ce signal. Le résultat est-il cohérent avec la donnée annoncée par le constructeur ? Justifier. T = 16,3 / 7 =2,33 ms ; f = 1 /(2,33 10-3) =430 Hz. Ecart relatif  ( 440-430) / 440 ~0,02 ( 2%). Donc valeurs cohérentes. 2. Numérisation d’un signal analogique. On enregistre le son émis par le diapason à l’aide d’un micro relié à un ordinateur. La tension aux bornes du micro est un signal analogique qui sera converti en signal numérique avant d’être stocké en mémoire. Un logiciel permet d’obtenir son spectre. 2.1. Parmi les spectres ci-dessous , lequel correspond au son enregistré ? Justifier. 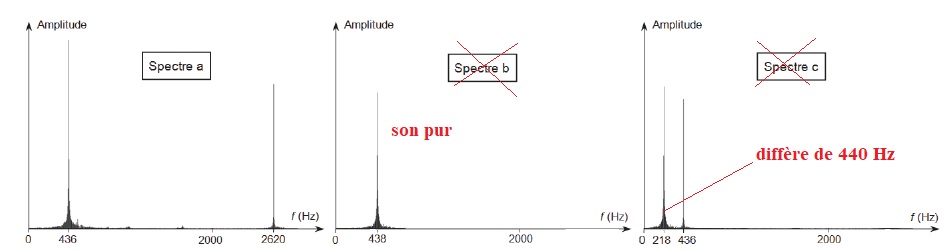2.2. Comment distingue-t-on un signal analogique d’un signal numérique ? Dans un signal analogique toutes les valeurs sont possibles. ( continuité ). Dans un signal numérique, seules un petits nombre de valeurs sont possibles ( discontinuité). La première étape de la conversion d’un signal analogique en signal numérique est appelée « échantillonnage ». Cette étape consiste à prélever à intervalle de temps régulier des valeurs du signal analogique. Cet intervalle de temps régulier est la période d’échantillonnage Te. Après quantification, chacune des valeurs échantillonnées se voit attribuer un nombre binaire codé sur N bits : c’est le codage. Le logiciel d’acquisition utilisé permet de choisir la durée totale Δt de l’enregistrement, la fréquence d’échantillonnage fe ainsi que le nombre N. Pour faciliter le transfert des données, on impose de réaliser un enregistrement dont la taille ne doit pas dépasser 500 ko. 2.3. Montrer qu’en choisissant Δt = 2,0 s, fe = 44 kHz et N = 32 bits, la condition sur la taille du fichier est respectée. Nombre d'échantillons = fréquence d'échantillonage fois durée ; 44 103 x 2,0 =  8,8 104 échantillons. Chaque échantillon est codé sur 4 octets. soit 8,8 104 x4 = 3,52 105 octets ~ 3,5 102 ko, valeur inférieure à 500 ko.  Quel est l’intérêt d’augmenter la valeur de la fréquence d’échantillonnage ? Quel serait l’inconvénient ? La conversion du signal est améliorée, mais la taille du fichier sera beaucoup plus grande.( temps de transfert plus long ). ........   3. Émission du son produit par un diapason à 440 Hz L’émission d’un son par un diapason est un phénomène complexe qui n’a été correctement décrit qu’au milieu du XXe siècle. 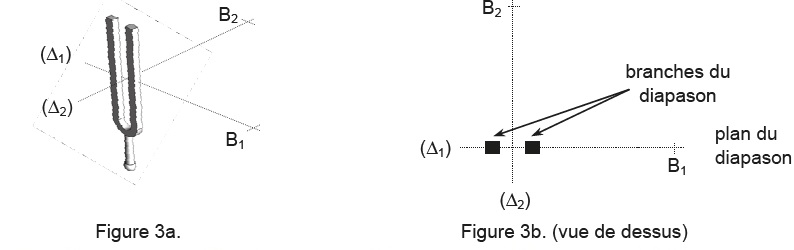3.1. Afin d’étudier la manière dont le son est émis autour d’un diapason, on dispose de deux sonomètres en B1 et B2 à 1,0 m du diapason (figures 3a et 3b sans souci d’échelle). Après avoir frappé le diapason, on relève au même instant les niveaux d’intensité sonore mesurés par chacun des sonomètres placés en B1 et B2 situés à 1,0 m du diapason. On obtient LB1 = 59 dB et LB2 = 42 dB. Soient IB1 et IB2 les intensités sonores mesurées à l’instant considéré aux points B1 et B2, vérifier que IB1 et IB2 sont reliés approximativement par la relation : IB2 = IB1/ 50. IB1 = I0 105,9 ; IB2 = I0 104,2 ; IB2 / IB1=104,2-5,9=10-1,7 =0,0199 ~ 1 /50. 3.2. On étudie le niveau d’intensité sonore à un mètre du diapason à 440 Hz en tournant autour de celui-ci. La position du sonomètre est repérée par l’angle θ dont l’origine correspond au plan du diapason (figure 4a). La courbe (figure 4b) représente l’atténuation de l’intensité sonore en fonction de l’angle θ. L’atténuation de l’intensité sonore est donnée par la relation : L – Lmax avec L, le niveau d’intensité sonore dans la direction repérée par l’angle θ et Lmax le niveau d’intensité sonore maximal. 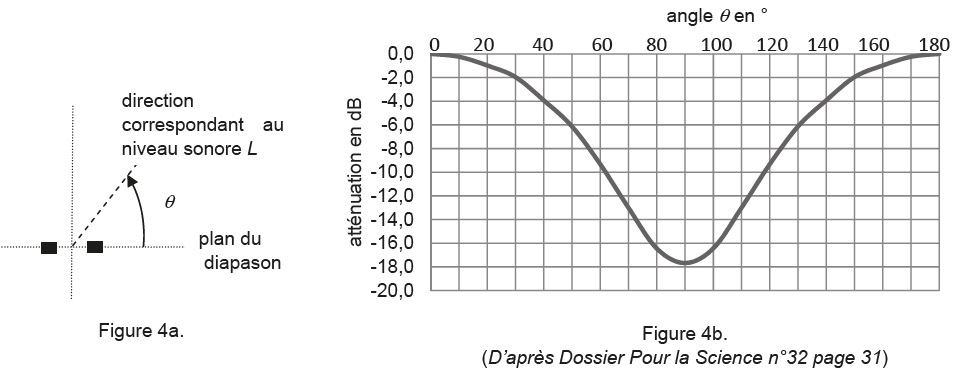Montrer quantitativement que les deux mesures précédentes, LB1 et LB2, sont cohérentes avec la courbe de la figure 4b. B1 est dans le plan du diapason, l'atténuation est nulle. B2 est dans une direction perpendiculaire au plan du diapason, l'atténuation est voisine de -18 dB. LB2 = 59-18 = 41 dB. Les mesures donnent LB2 = 42 dB.  Ces valeurs sont cohérentes. ..

menu