Fonctions
logarithme et exponentielle, bac S 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
......
.....
|
Amérique du nord.
Partie A : établir
une inégalité
Sur l’intervalle [0;+∞[ , on définit la fonction 𝑓 par
𝑓(𝑥)=𝑥−ln(𝑥+1).
1. Étudier le sens
de variation de la fonction 𝑓 sur l’intervalle [0;+∞[.
f '(x) = 1-1/(x+1) = x /(x+1), positive sur [0;+∞[.
f(x) est strictement croissante sur [0;+∞[.
2. En déduire que
pour tout 𝑥∈[0;+∞[, ln (𝑥+1)≤𝑥.
f(0) = 0 -ln(1) = 0.
De plus f(x) est strictement croissante.
par suite f(x) > 0
; ln (𝑥+1)≤𝑥.
Partie B :
application à l’étude d’une suite
On pose 𝑢 0=1 et pour tout entier naturel 𝑛, 𝑢 𝑛+1=𝑢 𝑛−ln
(1+𝑢 𝑛). On admet que la suite de terme général 𝑢 𝑛
est bien définie.
1. Calculer une
valeur approchée à 10 −3 près de 𝑢 2.
u 1 = u 0 -ln(1+u 0) = 1 - ln2 ~ 0,307
u 2 = u 1 -ln(1+u 1) ~ 0,307 -ln1,307 ~ 0,039.
2. a. Démontrer par
récurrence que pour tout entier naturel 𝑛, 𝑢 𝑛≥0.
Initialisation
: la propriété est vraie au rang zéro.
Hérédité :
la propriété est suposée vraie au rang p : 𝑢 p ≥0.
u p+1 =u p - ln(1+u p) ; or ln(1+u p)
< u p
; donc u p+1 >
0.
Conclusion :
la propriété est vraie au rang zéro et héréditaire, elle est donc vraie
quel que soit n.
b. Démontrer que
la suite (𝑢 𝑛) est décroissante, et en déduire que pour
tout entier naturel 𝑛, 𝑢 𝑛≤ 1 .
u n+1-u n = - ln(1+u n) avec n(1+u n)
>0 ;
donc u n+1 < u n.
La suite est décroissante.
c. Montrer que la
suite (𝑢𝑛) est convergente.
La suite est décroissante et minorée par 0, donc elle converge.
3. On note 𝑙 la
limite de la suite (𝑢 𝑛) et on admet que 𝑙=𝑓(𝑙) où 𝑓
est la fonction définie dans la partie A. En déduire la valeur de 𝑙.
l = l-ln(1+ l) ; ln(1+ l) = 0 = ln(1) ; l = 0.
4. a. Écrire un
algorithme qui, pour un entier naturel 𝑝 donné, permet de déterminer
le plus petit rang N à partir duquel tous les termes de la suite (𝑢 𝑛)
sont inférieurs à 10 −𝑝.
à U on affecte 1
à N on affecte 0
Tant que U > 10-p
à U on affecte U-ln(1+U)
N = N+1
Fin tant que.
b. Déterminer le
plus petit entier naturel 𝑛 à partir duquel tous les termes de la
suite (𝑢𝑛) sont inférieurs à 10 −15 .
u 0 = 1 ; u 1 = 1 -ln(2) = 0,307 ; u 2 =
0,307 -ln(1,307) = 3,9 10 -2 ; u 3 = 3,9 10 -2
-ln(1,039) = 7,4 10 -4 ;
u 4 = 7,4 10 -4 -ln(1+7,4 10 -4) = 1,013
10 -6 ; u 5 = 1,013 10 -6 -ln(1+1.013 10 -6)
= 5,131 10 -13 ;
u 6 = 5,131 10 -13 -ln(1+5,131 10 -13) =
1,58 10 -17 ;
n = 6.
Liban.
Le plan est muni d’un repère orthogonal .
1. On considère la fonction f définie sur l’intervalle ]0; 1] par
f (x) = x(1−lnx)
2
.
a. Déterminer une expression de la fonction dérivée de f et vérifier que pour tout x ∈]0 ; 1],
f
′
(x) = (lnx +1)(lnx −1).
On pose u = x et v = (1-ln x)2 ; u' = 1 ; v' = - 2(1-ln x) / x .
u'v +v'u = (1-ln x)2 -2(1-ln x) =(1-ln x) ( 1-ln x -2) = -(1-ln x)(1+ln x) =(lnx +1)(lnx −1).
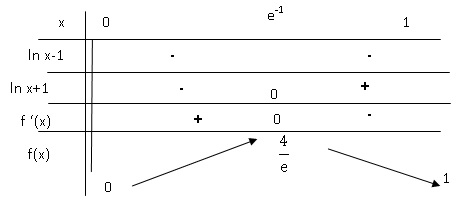
b. Étudier les variations de la fonction f et dresser son tableau de variations sur l’intervalle
]0; 1] (on admettra que la limite de la fonction f en 0 est nulle).
lnx-1 est négatif ;
ln x +1 = 0 ; ln x = -1 ; x = e-1.
On note Γ la courbe représentative de la fonction g définie sur l’intervalle ]0; 1] par g (x) = lnx.
Soit a un réel de l’intervalle ]0; 1]. On note Ma le point de la courbe Γ d’abscisse a et da la tangente à
la courbe Γ au point Ma . Cette droite da coupe l’axe des abscisses au point Na et l’axe des ordonnées
au point Pa .
On s’intéresse à l’aire du triangle ONaPa quand le réel a varie dans l’intervalle ]0; 1].
2. Dans cette question, on étudie le cas particulier où a = 0,2 et on donne la figure ci-dessous.
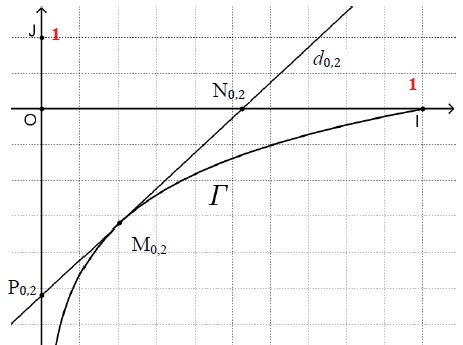
a. Déterminer graphiquement une estimation de l’aire du triangle ON0,2P0,2 en unités d’aire.
0,52 x2,6 / 2 = 0,676 unité d'aire.
b. Déterminer une équation de la tangente 𝑑0,2 .
Coefficient directeur : g'(0,2) = 1 / 0,2 = 5.
La tangente passe par le point M02 (0,2 ; ln(0,2) : y = 5 x0,2 +b = ln(0,2) = -ln(5) ; b = -1-ln(5).
y = 5x -1-ln 5.
c. Calculer la valeur exacte de l’aire du triangle ON0,2P0,2 .
OP02 =(1+ln 5) ; ON02 =(1+ln 5) / 5 ; Aire = (1+ln 5)2 / 10.
Dans ce qui suit, on admet que, pour tout réel 𝑎 de l’intervalle ]0
;1], l’aire du triangle ON𝑎P𝑎 en unités d’aire est donnée par :
𝐴(𝑎)=0,5𝑎 (1 –ln𝑎)2.
3. À l’aide des
questions précédentes, déterminer pour quelle valeur de 𝑎 l’aire
𝐴(𝑎) est maximale. Déterminer cette aire maximale.
f(x) passe par un maximum pour x = e-1.
L'aire est maximale pour x = e-1 et vaut : 0,5 e-1 (1+ln e)2 = 2 e-1.
|
...
|
|
Asie.
Partie A.
Soit 𝑎 et 𝑏 des nombres réels. On considère une fonction 𝑓 définie
sur [0 ; +∞[ par
𝑓(𝑥) =a / (1+e-bx).
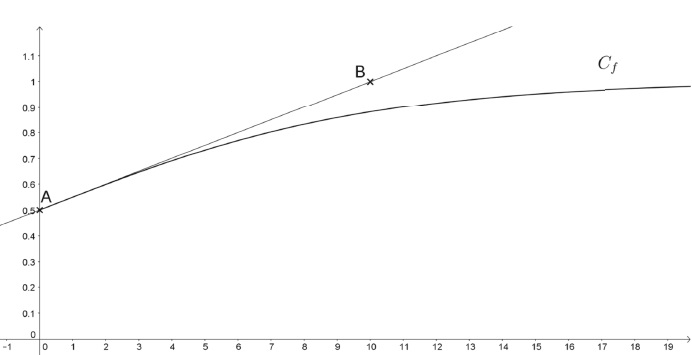
La courbe Cf représentant la fonction 𝑓 dans un repère
orthogonal est donnée ci-dessous.
La courbe Cf passe par le point A(0 ; 0,5).
La tangente à la courbe Cf au point A passe par le point
B(10 ; 1).
1. Justifier que a
= 1.
f(0) = 0,5 = a /(1+e0) = a / (1+1) =0,5 a ; a = 1.
On obtient alors, pour tout réel 𝑥 ≥ 0, f(x) =1 / (1+e-bx).
2. On admet que la
fonction f est dérivable sur [0 ; +∞[ et on note f ' sa fonction
dérivée.
Vérifier que, pour tout réel 𝑥 ≥ 0, f '(x) = be-bx / (1+e-bx)2.
On pose u = 1+e-bx ; u' = -be-bx
; f '(x) = -u' / u2 =
be-bx / (1+e-bx)2.
3. En utilisant
les données de l’énoncé, déterminer b
Equation de la tangente y = c x +d.
c = f '(0) = b / 4 ;
La tangente passe en A(0 ; 0,5) : 0,5 = d.
La tangente passe en B(10 ; 1) : 1 = 2,5b +0,5 ; b = 0,2.
Equation de cette tangente
: y = 0,05 x +0,5.
Partie B.
La proportion d’individus qui possèdent un certain type d’équipement
dans une population est modélisée par la fonction p définie sur [0 ;
+∞[ par p(x) =1 / (1 +e-0,2x)
Le réel x représente le temps écoulé, en année, depuis le 1er
janvier 2000.
Le nombre p(x) modélise la proportion d’individus équipés après x
années.
Ainsi, pour ce modèle, p(0) est la proportion d’individus équipés au 1er
janvier 2000 et p(3,5) est la proportion d’individus équipés au milieu
de l’année 2003.
1. Quelle est, pour
ce modèle, la proportion d’individus équipés au 1er janvier
2010 ? On en donnera une valeur arrondie au centième.
p(10) = 1 / (1 +e-2)=0,88.
2. a. Déterminer le
sens de variation de la fonction p sur [0 ; +∞[.
p '(x) = 0,2e-0,2x / (1+e-0,2x)2.
p'(x) étant strictement positive sur [0
; +∞[ , p(x) est strictement croissante sur cet intervalle.
b. Calculer la limite de la fonction
𝑝 en +∞.
Le terme en exponentielle tend vers zéro si x tend vers plus l'infini.
p(x) tend vers 1 si x tend vers plus l'infini.
c. Interpréter
cette limite dans le contexte de l’exercice.
Au bout d'un temps très long, tous les
individus sont équipés de ce matériel.
3. On considère que, lorsque la
proportion d’individus équipés dépasse 95 %, le marché est saturé.
Déterminer, en expliquant la démarche, l’année au cours de laquelle
cela se produit.
1 / (1 +e-0,2x) > 0,95 ; 1 +e-0,2x < 1 / 0,95 ; e-0,2x < 1 / 0,95 -1 ;
e-0,2x < 0,05 / 0,95 ;
La fonction logarithme étant strictement croissante sur [0
; +∞[.
-0,2x < ln(0,05 /
0,95) ; 0,2 x > ln
(0,95 / 0,05) ;
x > ln (19) / 0,2 ; x >14,7.
Courant 2014, le marché sera saturé.
En 2015, plus de 95 % des individus seront équipés.
4. On définit la proportion moyenne
d’individus équipés entre 2008 et 2010 par :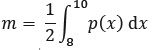
a. Vérifier que,
pour tout réel 𝑥 ≥ 0, p(x) =e0,2x / (1+e0,2x).
p(x) =1 / (1 +e-0,2x)
On multiplie numérateur et dénominateur par e0,2x : Par
suite p(x) =e0,2x / (1+e0,2x).
b. En déduire une
primitive de la fonction p sur [0 ; +∞[.
On pose u = 1 +e0,2x ; u' = 0,2e0,2x ; 5 u'
= e0,2x ; p(x) = 5 u' / u.
Une primitive de la fonction p est p(x) = 5 ln(u) = 5 ln (1+e0,2x).
c. Déterminer la
valeur exacte de 𝑚 et son arrondi au centième.
m = 2,5 [ ln(1+e2) -ln(1+e1,6)] ~0,86.
Antilles.
Soit g la fonction définie sur ]0 ; +∞[ par
g (x)= 4x −x ln x.
On admet que la fonction g est dérivable sur ]0 ; +∞[ et on note g ′ sa dérivée.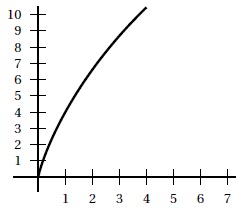
Partie A.
Le graphique ci-dessus représente une partie de la courbe
représentative de la fonction g obtenue par un élève sur sa
calculatrice. Cet élève
émet les deux conjectures suivantes :
• il semble que la fonction g soit positive;
• il semble que la fonction g soit strictement croissante.
L’objectif de cette partie est de valider ou d’invalider chacune de ces conjectures.
1. Résoudre l’équation g (x) = 0 sur l’intervalle ]0 ; +∞[.
x(4-ln(x))=0 ; solution retenue : ln(x) = 4 soit x =e4 ~55.
2. Déterminer le signe de g (x) sur l’intervalle ]0 ; +∞[.
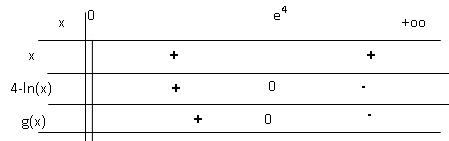
3. Les conjectures de l’élève sont-elles vérifiées ?
La première conjecture est vérifiée sur l'intervalle ]0 ; 6].
La fonction g ne peut pas être strictement croissante. La seconde conjecture est fausse.
Partie B.
Dans cette partie, on poursuit l’étude de la fonction g .
1. a. On rappelle que la limite en plus l'infini de ln(t) / t est égale àzéro.
En déduire que la limite en zéro de x ln(x) est égale à zéro.
ln (-x) = ln (1/x) ; x = 1 / (1/x) ; on pose t = 1/x ; -x ln(x) = -ln(t) / t.
Quand x tend vers 0+, t tend vers +oo et ln(t) / t tend vers zéro.
b. Calculer la limite de g (x) lorsque x tend vers 0.
4x tend vers zéro ; xln(x) tend vers zéro ; g(x) tend vers zéro.
2. a. Démontrer que, pour tout réel x strictement positif, g ′(x) = 3−lnx.
On pose u = x ; v = ln(x) ; u' = 1 ; v' = 1/x ; (uv)' = u'v+v'u = ln(x) +1.
g'(x) = 4-ln(x) -1 = 3 -ln(x).
b. Dresser le tableau de variations de la fonction g.
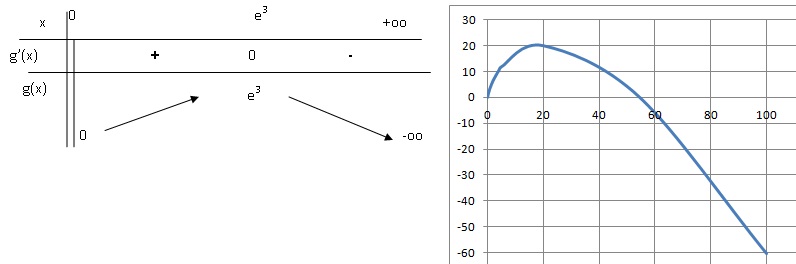
3. On désigne par G la fonction définie sur ]0 ; +∞[ par
G(x) =0,25 x2 (9-2ln(x))
On admet que la fonction G est dérivable sur ]0 ; +∞[.
a. Démontrer que la fonction G est une primitive de la fonction g sur ]0 ; +∞[.
On dérive G en posant u = 0,25 x2 et v = 9-2ln(x) ; u' =0,5x ; v' = -2 /x.
u'v+v'u = 0,5x(9-2ln(x)) -0,5x =0,5x(8-2ln(x) = x(4-ln(x)) = g(x).
b. L’affirmation suivante est-elle vraie?
« Il n’existe aucun réel α strictement supérieur à 1 tel que :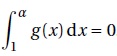
G(a) -G(1) =0,25 a2 (9-2ln(a))-2,25 =0.
a2 (9-2ln(a))- 9 =0 ; affirmation fausse.

|
....
|
Nlle Calédonie.
Soient f et g les fonctions définies sur ]0 ; +∞[ par f (x) = e−x et g (x) =1 / x2 e-1/x.
On admet que f et g sont dérivables sur ]0 ; +∞[. On note f ′ et g ′ leurs fonctions dérivées respectives.
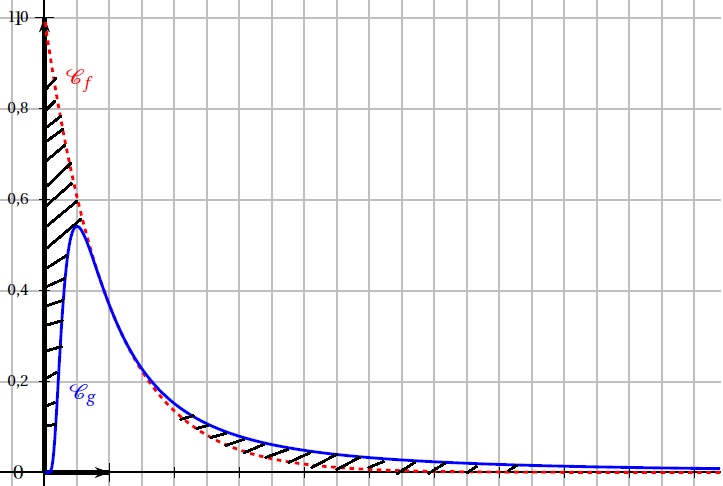
Les représentations graphiques de f et g dans un repère orthogonal, nommées respectivement Cf et Cg sont données ci-dessous
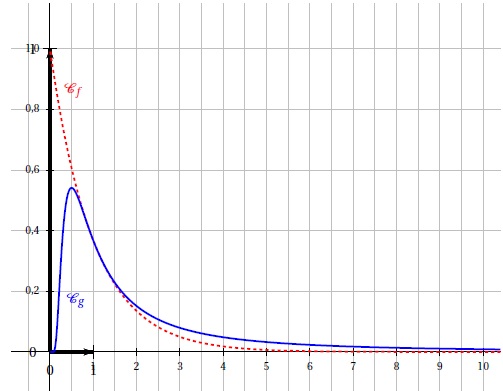
Partie A – Conjectures graphiques.
Dans chacune des questions de cette partie, aucune explication n’est demandée.
1. Conjecturer graphiquement une solution de l’équation f (x) = g (x) sur ]0 ; +∞[.
Abscisse de l'intersection des deux courbes : x = 1.
2. Conjecturer graphiquement une solution de l’équation g ′(x) = 0 sur ]0 ; +∞[.
Abscisse du maximum : x = 0,5.
Partie B – Étude de la fonction g.
1. Calculer la limite de g (x) quand x tend vers +∞.
1 / x tend vers zéro ; e-1/x tend vers e0 = 1 ; 1/x2 tend vers zéro ; produit des limites g(x) tend vers zéro.
2. On admet que la fonction g est strictement positive sur ]0 ; +∞[.
Soit h la fonction définie sur ]0 ; +∞[ par h(x) = ln(g (x)).
a. Démontrer que, pour tout nombre réel x strictement positif,
h(x) =(−1−2x ln(x) ) / x.
ln(1 / x2 e-1/x)=ln(1 / x2) +ln(e-1/x) = -ln(x2) -1 /x = -2ln(x) -1 / x = (-2x ln(x)-1) / x.
b. Calculer la limite de h(x) quand x tend vers 0.
x ln(x) tend vers zéro ;(-2x ln(x)-1) tend vers -1 ; -1 / x tend vers moins l'infini.
h(x) tend vers moins l'infini quand x tend vers zéro.
c. En déduire la limite de g (x) quand x tend vers 0.
g(x) = eh(x) ; eh(x) tend vers zéro quand x tend vers zéro.
3. Démontrer que, pour tout nombre réel x strictement positif,
g ′(x) =e− 1/x (1−2x) / x4 .
On pose u = 1 /x ; u' = -1 /x2.
g(x) = u2 e-u ; on pose v = u2 et w = e-u ;
v' = 2uu' = -2/ x3 ; w' = -e-u u'= e-1/x/x2.
v' w + w' v = -2e-1/x / x3 +e-1/x / x4 =e-1/x/ x4 (1-2x)
4. En déduire les variations de la fonction g sur ]0 ; +∞[.
e-1/x/ x4 est toujours positif.
Le signe de g'(x) est celui de (1-2x).
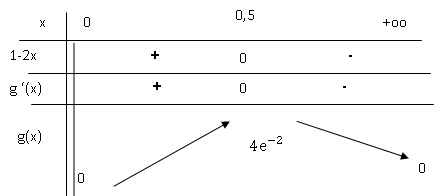
Partie C – Aire des deux domaines compris entre les courbes Cf et Cg.
1. Démontrer que la point A de coordonnées (1 ; e−1) est un point d’intersection de Cf et Cg .
On admet que ce point est l’unique point d’intersection de Cf et Cg , et que Cf est au dessus de Cg sur l’intervalle ]0 ; 1[ et en dessous sur l’intervalle ]1 ; +∞[.
e−x = 1 / x2 e-1/x ; e−x = 1 / (x2 e1/x ) ; x2 e-x e1/x = 1 ;
ln(x2) +ln(e-x) + ln(e1/x) = ln(1) = 0 ;
2ln(x) -x +1/x = 0 ; solution de cette équation x = 1 ; par suite f(1)=g(1) = e-1.
2. Soient a et b deux réels strictement positifs. Démontrer que
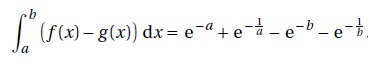
On pose u = 1 / x ; u' = -1/x2 : g(x) = -u' e-u ; primitive de g(x) :e-u =e-1/x ;
primitive de f(x) : -e-x.
Par suite : [-e-x -e-1/x]ba = -e-b -e-1/b +e-a +e-1/a.
3. Démontrer que 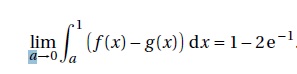
Quand a tend vers zéro : e-a tend vers 1 ; e-1/a tend vers zéro ;
Quand b est égal à 1 : -e-b = -e-1 et -e-1/b = -e-1 ;
par suite -e-b -e-1/b +e-a +e-1/a tend vers 1-2e-1.
4. On admet que
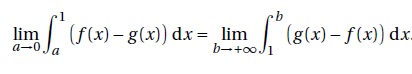
Interpréter graphiquement cette égalité.
Les aires hachurées sont égales.
Amérique du sud.
La vasopressine est une hormone favorisant la réabsorption de l’eau par l’organisme.
Le taux de vasopressine dans le sang est considéré normal s’il est inférieur à 2,5 μg/mL.
Cette hormone est sécrétée dès que le volume sanguin diminue. En
particulier, il y a production de vasopressine suite à une hémorragie.
On utilisera dans la suite la modélisation suivante :
f (t ) = 3te-0,25t +2 avec t >0,
où f (t ) représente le taux de vasopressine (en μg/mL) dans le sang en
fonction du temps t (en minute) écoulé après le début d’une hémorragie.
1. a. Quel est le taux de vasopressine dans le sang à l’instant t = 0 ?
f(0) = 2 µg / mL.
b. Justifier que douze secondes après une hémorragie, le taux de vasopressine dans le sang n’est pas normal.
12 s ou 12 / 60 = 0,2 minute.
f(0,2) = 3 x0,2 exp(-0,25 x0,2) +2 = 2,57 µg / mL, valeur supérieure à 2,5 µg / mL.
c. Déterminer la limite de la fonction f en +∞. Interpréter ce résultat.
Le terme en exponentielle tend vers zéro si t tend vers plus l'infini.
3te-0,25t tend vers zéro et f(t) tend vers 2.
Au bout d'un temps suffisamment long le taux de vasopresine dans le sang tend vers 2 µg / mL.
2. On admet que la fonction f est dérivable sur [0 ; +∞[.
Vérifier que pour tout nombre réel t positif,
f ′(t )=0,75 (4-t) e-0,25t .
On pose u = 3t et v = e-0,25t ; u' = 3 et v' = -0,25 e-0,25t ;
u'v + v' u = 3e-0,25t -0,75t e-0,25t = (3-0,75 t)e-0,25t =0,75 (4-t) e-0,25t .
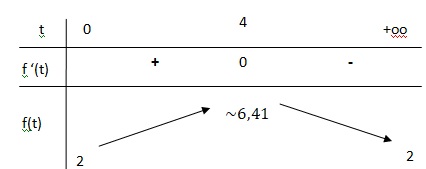
3. a. Étudier le sens de
variation de f sur l’intervalle [0 ; +∞[ et dresser le tableau de
variations de la fonction f (en incluant la limite en +∞).
e-0,25t est positif ; le signe de f '(t) est celui de 4-t.
Si t < 4, f '(t) est positive et f(t) est croissante.
Si t >4, f '(t) est négative et f(t) est décroissante.
Si t = 4, f '(t) est nulle est f(t) présente un maximum.
b. À quel instant le taux de vasopressine est-il maximal ?
Quel est alors ce taux ? On en donnera une valeur approchée à 10−2 près.
4. a. Démontrer qu’il existe une unique valeur t0 appartenant à [0; 4] telle que f (t0) = 2,5.
En donner une valeur approchée à 10−3 près.
Sur cet intervalle, f(t) est continue ( car dérivable) et strictement croissante ; f(0) = 2 et f(4) ~6,41 µg / mL.
D'après le théorème de la bijection, l'équation f(t0) = 2,5 admet une unique solution sur cet intervalle.
t0 ~0,174 minute.
On admet qu’il existe une unique valeur t1 appartenant à [4 ; +∞[ vérifiant f (t1) = 2,5.
On donne une valeur approchée de t1 à 10−3 près : t1 ≈ 18,930.
b. Déterminer
pendant combien de temps, chez une personne victime d’une hémorragie,
le taux de vasopressine reste supérieur à 2,5 μg/mL dans le sang.
t1-t0 = 18,930 -0,174 ~18,756 minutes.
5. Soit F la fonction définie sur [0 ; +∞[ par F(t ) = −12(t +4)e−0,25t +2t .
a. Démontrer que la fonction F est une primitive de la fonction f et en déduire une valeur approchée de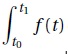 à l’unité près. à l’unité près.
On pose u = t+4 et v = e-0,25t ; u' = 1 et v' = -0,25 e-0,25t ;
u'v + v' u = e-0,25t -0,25(t+4) e-0,25t = -0,25 t e-0,25t .
F'(t) = 12 x0,25 t e-0,25t +2 = 3t e-0,25t +2 = f(t).
b. En déduire une
valeur approchée à 0,1 près du taux moyen de vasopressine, lors d’un
accident hémorragique durant la période où ce taux est supérieur à 2,5
μg/mL.
(F(t1-F(t0) ) / (t1-t0).
F(18,93)= -12x22,93 exp(-0,25 x18,93) +2 x18,93 ~35,43.
F(0,174)= -12x4,174 exp(-0,25 x0,174) +2 x0,174 ~-47,608.
(35,43 -(- 47,608)) / 18,756 ~4,4 µg / mL.
|
|