Mathématiques,
bac S Centres étrangers 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
| .
. |
Exercice 1 : Commun à tous les
candidats (4 points)
Cet exercice est un questionnaire à choix multiples (Q.C.M.) qui envisage quatre situations relatives à une station de ski.
Les quatre questions sont indépendantes.
Pour chacune des questions, une seule des quatre réponses est exacte.
Le candidat indiquera sur sa copie le numéro de la question et la
lettre correspondant à la réponse exacte. Aucune justification n’est
demandée. Une réponse exacte rapporte un point, une réponse fausse ou
une absence de réponse ne rapporte ni n’enlève aucun point.
1. Une étude statistique a établi qu’un client sur quatre pratique le surf.
Dans une télécabine accueillant 80 clients de la station, la
probabilité arrondie au millième qu’il y ait exactement 20 clients
pratiquant le surf est :
a) 0,560; b) 0,25; c) 1 ; d) 0,103.
La variable aléatoire X représente le nombre de surfeurs.
Les événements sont indépendants, identiques ; chaque tirage a deux issues possibles.
X suit la loi de Bernoulli de paramètre n = 80 et p = 0,25.
p(X = 20) ~ 0,103
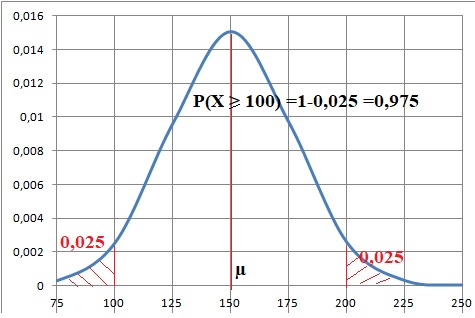
2. L’épaisseur
maximale d’une avalanche, exprimée en centimètre, peut être modélisée
par une variable aléatoire X qui suit une loi normale de moyenne μ =
150 cm et d’écart-type inconnu.
On sait que P( X > 200) = 0,025. Quelle est la probabilité P( X >100) ?
a) On ne peut pas répondre car il manque des éléments dans l’énoncé.
b) 0,025 ; c) 0,95 ; d) 0,975.
3. Dans un couloir
neigeux, on modélise l’intervalle de temps séparant deux avalanches
successives, appelé temps d’occurrence d’une avalanche, exprimé en
année, par une variable aléatoire T qui suit une loi exponentielle.
On a établi qu’une avalanche se déclenche en moyenne tous les 5 ans. Ainsi E (T ) = 5 .
La probabilité P(T > 5) est égale à :
a) 0,5 ; b) 1 e−1 ; c) e−1 ; d) e−25.
l = 1 / 5 = 0,2.
P(T > 5) = e-5l = e-1.
4.
L’office de tourisme souhaite effectuer un sondage pour estimer la
proportion de clients satisfaits des prestations offertes dans la
station de ski. Pour cela, il utilise un intervalle de confiance de
longueur 0,04 avec un niveau de confiance de 0,95.
Le nombre de clients à interroger est :
a) 50 ; b) 2 500 ; c) 25 ; d) 625.
Longueur de l'intervalle de confiance : 2 / n½ = 0,04 ; n = (2 /0,04)2 = 2500.
Exercice 2 ( 6 points ).
Le but de cet exercice est d’étudier la suite (un) définie par la donnée de son premier terme u1 et, pour tout entier naturel n supérieur ou égal à 1, par la relation :
un+1 = (n+1) un-1.
Partie A.
1. Vérifier, en détaillant le calcul, que si u1 = 0 alors u4 = −17
u2 = (1+1) u1-1=-1 ;
u3 = (2+1) u2-1=-4 ;
u4 = (3+1) u3-1=-17.
2. Recopier et compléter l’algorithme ci-dessous pour qu’en saisissant préalablement dans U une valeur de u1 , il calcule les termes de la suite (un ) de u2 à u13
U = "valeur de u1".
Pour N allant de 1 à 12
U = (N+1) *U-1
Fin Pour
3. On a exécuté cet algorithme pour u1 = 0,7 puis pour u1 = 0,8 . Voici les valeurs obtenues.
Pour u1 = 0,7
|
0,4
|
0,2
|
-0,2
|
-2
|
-13
|
-92
|
-737
|
-6634
|
-729752
|
-8757025
|
Pour u1 = 0,8
|
0,6
|
0,8
|
2,2
|
10
|
59
|
412
|
3295
|
29654
|
296539
|
3261928
|
Quelle semble être la limite de cette suite si u1 = 0,7 et si u1 = 0,8 ?
Si u1 = 0,7 la suite tend vers moins l'infini et si u1 = 0,8 la suite tend vers plus l'infini.
Partie B.
On considère la suite ( In) définie pour tout entier naturel n, supérieur ou égal à 1, par :
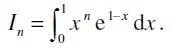
On rappelle que le nombre e est la valeur de la fonction exponentielle en 1, c’est-à-dire que e = e1 .
1. Prouver que la fonction F définie sur l’intervalle [0;1] par F(x) =(-1-x)e1-x est une primitive sur l’intervalle [0;1] de la fonction f définie sur l’intervalle [0;1] par f(x) = xe1-x.
Dériver F(x) en posant u = -1-x et v = e1-x ; u' = -1 ; v' = -e1-x ;
u'v + v'u = -e1-x +(1+x)e1-x = xe1-x = f(x).
2. En déduire que I1 = e − 2 .
I1 = F(1) -F(0) = (-1-1)e1-1 - (-1-0)e1-0 = -2+e.
3. On admet que, pour tout entier naturel n supérieur ou égal à 1, on a :
In+1 = (n+1)In-1.
Utiliser cette formule pour calculer I2 .
I2 = (1+1)I1-1 = 2(e-2)-1=2e-5.
4. a)
Justifier que, pour tout nombre réel x de l’intervalle [0;1] et pour
tout entier naturel n supérieur ou égal à 1, on a : 0 < xne1-x < xne.
0 < x <1 ; 0 > -x > -1 ; 0+1 > -x+1 > -1 +1 ; 1 > -x+1 > 0 ou encore 0 < -x+1 < 1.
La fonction exponentielle étant strictement croissante sur R :
e0 =1 < e1-x < e1.
Multiplier par xn strictement positif :
xn < xne1-x < xne1.
cette inégalité est aussi vérifiée pour x = 0.
b) Justifier que :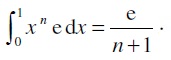
Une primitive de xn est xn+1 / (n+1) ;
pour n > 1, une primitive de e xn est e xn+1 / (n+1) ;
par suite sur l'intervalle [0 ; 1 ] : e 1n+1 / (n+1)- e 0n+1 / (n+1) = e / n+1).
.
c) En déduire que, pour tout entier naturel n supérieur ou égal à 1, on a : 0 < In < e /(n+1).
D'après la question B.4.a : 0 < xne1-x < xne.
Intégrer sur [0 ; 1] cette inégalité : 0 < In < e /(n+1)..
d) Déterminer la limite de In en plus l'infini.
D'après le théorème d'encadrement In tend vers zéro si n tend vers plus l'infini.
Partie C.
Dans cette partie, on note n! le nombre défini, pour tout entier naturel n supérieur ou égal à 1, par :
1!=1
2!= 2×1
et si n > 3 :
n!= n x (n −1)×....×1
On a ainsi par exemple
3!= 3×2×1= 3×(2×1) = 3×2!
4!= 4×3×2×1= 4×(3×2×1) = 4×3!
8!= 8×7×6×5×4×3×2×1= 8×(7×6×5×4×3×2×1) = 8×7!
Et, plus généralement :
(n +1)! = (n +1)× n!
1. Démontrer par récurrence que, pour tout entier naturel n supérieur ou égal à 1, on a : un =n!(u1-e+2)+In.
On rappelle que, pour tout entier naturel n supérieur ou égal à 1, on a :
un+1 = (n+1) un -1 et In+1 =(n+1)In-1.
Inittialisation : I2 = 2e-5 ; u2 = 2u1-1 ; u2-I2 =2u1-1-2e+5 =2u1+4-2e = 2(u1+2-e) =2!(u1+2-e).
u2 =2!(u1+2-e)+I2. La relation est vraie au rang 2.
Hérédité : la relation est supposée vraie au rang p : up =p!(u1-e+2)+Ip.
(p+1)up =(p+1)p!(u1-e+2)+(p+1)Ip.
(p+1)up -1=(p+1)p!(u1-e+2)+(p+1)Ip-1.
Or (p+1)p! = (p+1)!.
up+1=(p+1)! (u1-e+2)+Ip+1-1.
La relation est vraie au rang p+1.
Conclusion : la relation est vraie au rang 2 et héréditaire, elle est vraie pour tout entier n supérieur ou égal à 1.
2. On admet que la limite en plus l'infini de n! est égale à plus l'infini.
a) Déterminer la limite de la suite (un ) lorsque u1 = 0,7 .
un =n!(0,7-e+2)+In = n!(2,7-e)+In.
In tend vers zéro si n tend vers plus l'infini ; la limite en plus l'infini de n! est égale à plus l'infini.
De plus 2,7-e est négatif.
Si u1 = 0,7 la suite tend vers moins l'infini
b) Déterminer la limite de la suite ( un) lorsque u1 = 0,8 .
un =n!(0,8-e+2)+In = n!(2,8-e)+In.
In tend vers zéro si n tend vers plus l'infini ; la limite en plus l'infini de n! est égale à plus l'infini.
De plus 2,8-e est positif.
Si u1 = 0,8 la suite tend vers plus l'infini
|
|
|
Exercice 3 : Commun à tous les candidats (5 points)
Le plan est muni d’un repère orthonormé direct.
Le but de cet exercice est de déterminer les nombres complexes � non nuls tels que les points d’affixes 1, z2 et 1/z soient alignés.
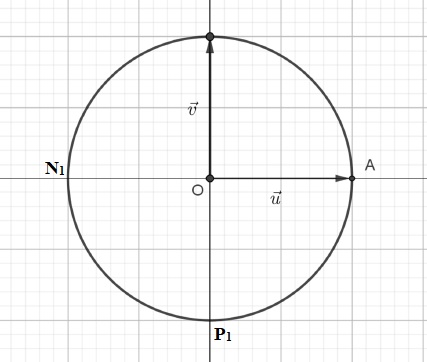
Sur le graphique fourni, le point A a pour affixe 1.
Partie A : étude d’exemples.
1. Un premier exemple
Dans cette question, on pose : z = i .
a) Donner la forme algébrique des nombre complexes z2 et 1 /z.
z2 = i2 = -1.
1/z = 1 /i = i / i2 = -i..
b) Placer les points N1 d’affixe z2 et P1 d’affixe 1/z sur le graphique.
On remarque que dans ce cas les points A, N1 et P1 ne sont pas alignés.
2. Une équation
Résoudre dans l’ensemble des nombres complexes l’équation d’inconnue z : z2 + z +1 = 0 .
D = 12-4 = -3 = 3 i2.
z1 = (-1 +3½i) /2 ; z1 = (-1 -3½i) /2 ;
3. Un deuxième exemple
Dans cette question, on pose : z = (-1 +3½i) /2
a) Déterminer la forme exponentielle de z, puis celles des nombres complexes z2 et 1 / z.
|z |=(1 +3)½ /2 = 1.
z / |z|= -0,5 +i 3½/2 = cos (2p/3) + i sin(2p/3) =exp(i 2p/3 ).
z2 = exp(i 4p/3 ).
1 /z = exp( -i 2p/3 ).
.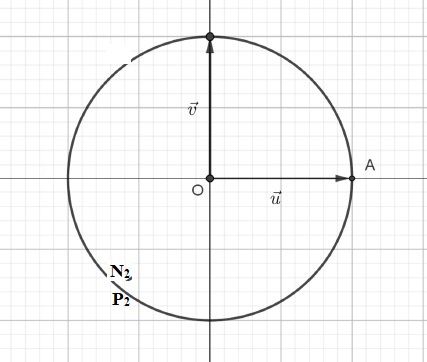
b) Placer les points N2 d’affixe z2 et P2 d’affixe 1 /z sur le graphique.
On remarque que dans ce cas les points A, N2 et P2 sont alignés.
Partie B : étude du cas général
Soit z un nombre complexe non nul.
On note N le point d’affixe z2 et P le point d’affixe 1 /z.
1. Établir que, pour tout nombre complexe z différent de 0, on a :
z2 -1 /z = (z2+z+1)(1-1/z).
On dévellope :(z2+z+1)(1-1/z) = z2-z+z-1+1-1/z =
z2 -1 /z.
2. On rappelle que :
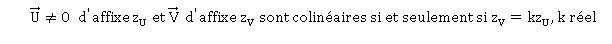
En déduire que, pour z différent de zéro, les points A, N et P définis ci-dessus sont alignés si et seulement si z2 + z +1 est un réel.
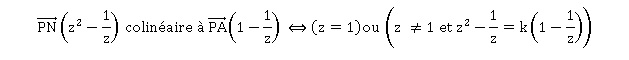
Si z diffère de 1 : (z2+z+1)(1-1/z) = k(1-1 / z) ;
z2+z+1 = k ; k étant réel, alors z2+z+1 est réel.
De plus si z = 1 ; z2+z+1 =3, nombre réel.
Donc, les points A, N et P définis ci-dessus sont alignés si et seulement si z2 + z +1 est un réel.
3. On pose z = x + i y , où x et y désignent des nombres réels.
Justifier que : z2 + z +1= x2 − y2 + x +1+ i (2xy + y) .
(x+iy)2 +x+iy +1 = x2 +i2y2+2ixy +x+iy+1=x2 − y2 + x +1+ i (2xy + y).
4. a) Déterminer l’ensemble des points M d’affixe z différent de zéro tels que les points A, N et P soient alignés.
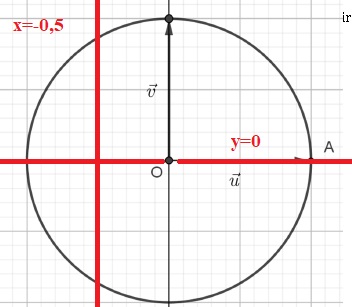
b) Tracer cet ensemble de points sur le graphique donné.
z2 + z +1 doit être un réel ;
donc x2 − y2 + x +1+ i (2xy + y) doit être un nombre réel : 2xy + y = 0.
y(2x+1)=0 ; y = 0 ou x = -½.
L'ensemble des points M est constitué des droites d'équation y = 0 et x = -0,5, privé de zéro.
|
|
|
|
Exercice 4 : Commun à tous les
candidats (5 points)
Dans l’espace, on considère un cube ABCDEFGH de centre Ω et d’arête de longueur 6.
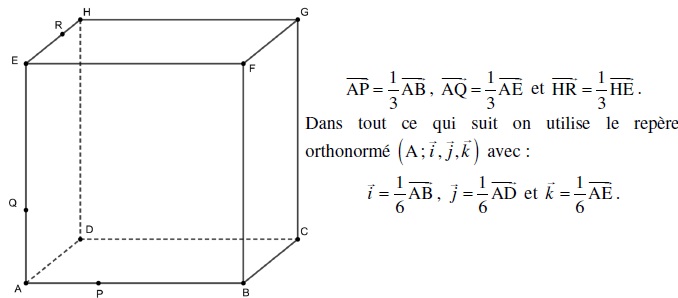
.
Dans ce repère, on a par exemple : B(6;0;0) , F(6;0;6) et R(0;4;6) .
1. a) Donner, sans justifier, les coordonnées des points P, Q et Ω.
P(2 ; 0 ; 0) ; Q(0 ; 0 ; 2) ; W(3 ; 3 ; 3 ).
b) Déterminer les nombres réels b et c tels que 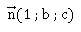 soit un vecteur normal au plan (PQR). soit un vecteur normal au plan (PQR).
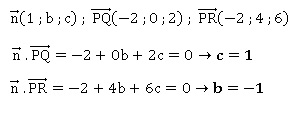
c) En déduire qu’une équation du plan (PQR) est : x − y + z − 2 = 0 .
Equation de ce plan : x -y +z +d = 0.
P(2 ; 0 ; 0) appartient à ce plan : 2-0+0+d = 0 ; d = -2.
x-y+z-2=0.
2. a) On note Δ la droite perpendiculaire au plan (PQR) passant par le point Ω, centre du cube.
Donner une représentation paramétrique de la droite Δ.
Le vecteur 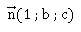 est un vecteur directeur de la droite. est un vecteur directeur de la droite.
x = t +xW ; y =- t +yW ; z = t +zW ;
x = t+3 ; y = -t+3 ; z = t+3.
b) En déduire que la droite Δ coupe le plan (PQR) au point I de coordonnées ( 8 /3 ; 10 /3 ; 8 / 3 ).
xM -yM +zM-2=0.
t+3 -(-t+3) +t+3 -2 = 0 ; 3t+1 = 0 ; t = -1 /3.
xM = -1 / 3+3 =8 /3 ; yM =1 /3 +3 = 10 / 3 ; zM=-1 /3 +3 = 8 /3.
c) Calculer la distance WI .
[(8 /3 -3)2 +(10 /3 -3)2 +(8 /3 -3)2 ]½ =(1 /9 +1/9 +1/9)½ =1 /3½.
3. On considère les points J(6;4;0) et K(6;6;2) .
a) Justifier que le point J appartient au plan (PQR) .
Les coordonnées du point J doivent vérifier l'équation du plan ( PQR) :
xJ -yJ +zJ-2= 6 -4+0-2 =0.
b) Vérifier que les droites (JK) et (QR) sont parallèles.
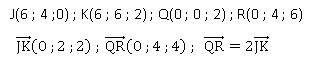
Ces deux vecteurs étant colinéaires, les droites (JK) et (QR) sont parallèles.
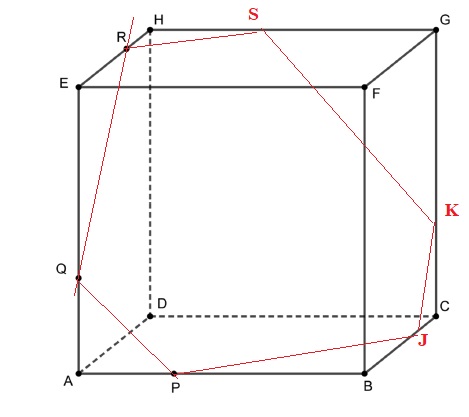
c) Sur la figure donnée, tracer la section du cube par le plan (PQR) .
On laissera apparents les traits de construction, ou bien on expliquera la démarche.
Placer le point J (6 ; 4 ; 0).
Tracer la parallèle à la droite (QR) passant par J. Elle coupe la droite (GC) en K.
Tracer la parallèle à la droite (PJ) passant par R. Elle coupe la droite (HG) en S.
|
|
|