Une
céramique comme réservoir d'énergie, bac S Amérique du sud 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
| .
. |
......
.....
|
Des chercheurs de l'Université de
Tokyo ont découvert une céramique capable de stocker de l’énergie. Son principe de fonctionnement est extrêmement simple ;
une courte exposition au Soleil permet de la « charger » ! Cette énergie peut être
stockée pendant une longue durée et restituée selon les besoins.
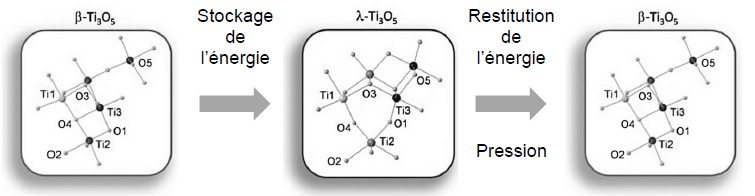
Le secret de ce matériau (pentoxyde de trititane, Ti3O5) réside dans sa
structure. En effet, sous certaines conditions (élévation de la température, exposition à un
rayonnement électromagnétique, application d’un courant électrique…), le matériau
change de structure
cristalline ; l’énergie reçue permet le passage du
beta-pentoxyde de trititane (𝛽-Ti3O5) au lambda-pentoxyde de trititane (𝜆-Ti3O5). Cette
nouvelle structure est stable.
Pour restituer l’énergie, il suffit de soumettre ce matériau à une
certaine pression.
Données
Constante de Planck : h = 6,63×10-34 J.s
Intensité de la pesanteur : g = 9,81 m.s-2
Volume V d’un cylindre de base circulaire de rayon r et de hauteur H : V = p. r 2.H
Surface S d’un disque de rayon R : S = p.R 2
Caractéristiques de la pastille cylindrique de pentoxyde de trititane
utilisée dans les expériences présentées dans cet exercice :
Diamètre : 13,0 mm. Épaisseur : 0,500 mm. Masse : 0,265 g
D’après Tokoro, H. et al. (2015). External stimulation-controllable heat-storage ceramics.
Nature communications. 6. 7037. 10.1038/ncomms8037.
1. Stockage de l’énergie.
Pour modifier la structure cristalline du pentoxyde de trititane, on
utilise un laser. L’énergie électromagnétique du faisceau de lumière
permet de modifier les liaisons à l’intérieur du cristal. Au cours de
cette étape, l’énergie du rayonnement doit être focalisée sur la
pastille de pentoxyde de trititane.
Pour modifier sa structure cristalline et effectuer le passage du 𝛽-Ti3O5 au 𝜆-Ti3O5, le matériau doit recevoir une énergie volumique E = 230 J.cm-3.
1.1. Parmi les
schémas suivants, identifier celui qui illustre le stockage de
l’énergie par le pentoxyde de trititane. Justifier votre réponse.
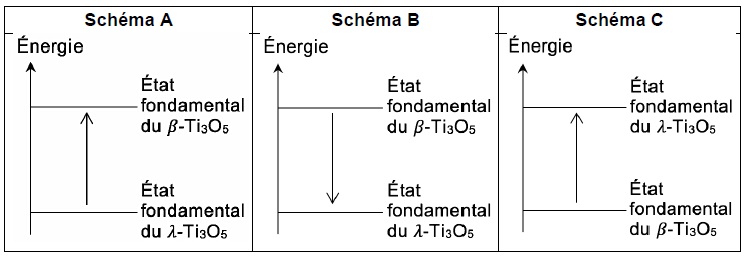
L’énergie reçue par le
beta-pentoxyde de trititane (𝛽-Ti3O5) permet le passage au lambda-pentoxyde de trititane (𝜆-Ti3O5). Cette
nouvelle structure est stable. Le schéma A ne convient pas.
Dans son état fondamental, le lambda-pentoxyde de trititane (𝜆-Ti3O5) a une énergie supérieure à celle de l'état fondamental du
beta-pentoxyde de trititane (𝛽-Ti3O5). Le schéma C convient.
1.2.
Sachant que la totalité de la surface de la pastille est éclairée,
vérifier que l’énergie qu’il faut fournir à la pastille utilisée dans
l’expérience vaut Ep = 15,3 J.
Volume de la pastille : V = p. r 2.H =3,14 x 0,652 x0,05 ~ 0,066 cm3.
Energie reçue : 0,066 x 230 ~ 15,3 J.
|
|
.
|
....
|
Caractéristiques du laser utilisé.
Longueur d’onde du rayonnement : 𝜆 = 410 nm
Débit de photons : il correspond à un nombre de photons reçu par le matériau par unité de temps.
DLaser = 1021 photons par seconde ; DSoleil = 1017 photons par seconde
1.3. En utilisant vos connaissances, citer une propriété du laser qui justifie son utilisation dans cette expérience.
Le faisceau laser étant très directif, la densité énergétique ( énergie par unité de surface) est très grande.
1.4. Calculer le nombre de photons nécessaires pour fournir l’énergie Ep à la pastille.
Energie d'un photon : E = h c / l = 6,63×10-34 x 3,00 108 / (410 10-9) ~4,85 10-19 J.
Nombre de photons : 15,3 / (4,85 10-19) ~3,15 1019.
1.5. Donner
l’ordre de grandeur de la durée minimale d’irradiation de la pastille
par le laser pour permettre la transition 𝛽-Ti3O5 → 𝜆-Ti3O5 et commenter la phrase : « une courte exposition au Soleil permet de la « charger » ! ».
Durée minimale d'irradiation par le laser : 3,15 1019 / 1021 ~0,03 s.
Durée minimale d'irradiation par le soleil : 3,15 1019 / 1017 ~300 s ou 5 minutes..
5 minutes correspond à une courte exposition au soleil.
2. Restitution de l’énergie.
Pour libérer l’énergie stockée au sein de la structure cristalline, il
suffit d’exercer une pression sur le matériau qui va entraîner une
réorganisation de la structure en provoquant la transition 𝜆-Ti3O5 → 𝛽-Ti3O5.
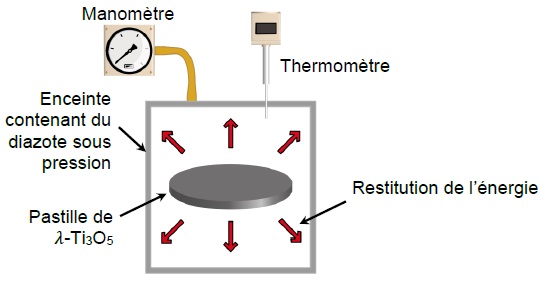
Le dispositif utilisé pour les tests en laboratoire est une enceinte
dans laquelle du diazote est mis sous pression que l’on peut faire
varier.
Variation d’énergie interne d’un gaz parfait
En faisant l’hypothèse que le diazote contenu dans l’enceinte est un
gaz parfait, la variation d’énergie interne ΔU du gaz s’exprime grâce à
la relation :
ΔU =2,5 .ngaz.R.ΔT
ΔU désigne la variation d’énergie interne du gaz (J)
ngaz désigne la quantité de matière de gaz présente dans l’enceinte (mol)
R désigne la constante des gaz parfaits, R = 8,31 J.K-1.mol-1
ΔT désigne la variation de température du gaz (K)
2.1. Que représente l’énergie interne d’un système ?
L'énergie
interne est l'énergie emmagasinée par un système, autre que l'énergie
cinétique macroscopique et l'énergie potentielle due à l'action des
corps extérieurs.
L'énergie interne est la somme de l'énergie cinétique microscopique de
chaque entité du système et de l'énergie potentielle d'interactions
entre les entités élémentaires du système.
Au
cours de l’expérience, l’enceinte utilisée est considérée comme
parfaitement isolée thermiquement. Elle contient 40,0 mmol de diazote.
Lorsque la pression P est exercée, la pastille restitue l’énergie
stockée qui entraîne une élévation de température du gaz de 18,2 K.
L’équilibre thermique est alors atteint.
2.2. Calculer l’énergie Q restituée par la pastille au cours de l’expérience.
ΔU =2,5 .ngaz.R.ΔT = 2,5 x 40,0 10-3 x8,31 x18,2 ~15,1 J.
2.3.
En considérant que les échanges thermiques s’effectuent sans perte,
calculer la masse de pentoxyde de trititane nécessaire pour chauffer
250 mL d’eau pure depuis la température ambiante jusqu’à 80°C.
Commenter le résultat obtenu en dégageant l’intérêt de ce matériau.
Données :Capacité thermique massique de l’eau liquide ceau = 4,18 J.g-1.°C-1.
Masse volumique de l’eau 𝜌eau = 1,00 g.mL-1.
Estimation de la température initiale de l'eau : 15 °C.
Energie reçue par 250 g d'eau pour l'ammener de 15°C à 80 °C :
Q = 250 x 4,18 x(80-15) ~6,8 104 J.
0,265 g de cette pastille libère 15,3 J.
6,8 104 /15,3 x 0,265 ~1,2 103 g = 1,2 kg.
L'énergie solaire étant intermittente, ces pastilles permettent
de stocker cette énergie renouvelable sur une longue période.
|
|


