Fonctions logarithme et exponentielle,concours avenir

Fonctions logarithme et exponentielle, Concours Advance.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

......

.....

2019.
4. Soit f la fonction définie sur R par f(x) = xe^1−x et C la courbe représentant f dans un repère orthonormé.
Soit d la droite d’équation y = e x + 15 et D la droite d’équation y = x.
A. La limite en plus l'infini de f(x) est égale à plus l'infini. Faux.
e^1-x tend vers zéro quand x tend vers plus l'infini.
B. La limite en moins l'infini de f(x) est égale à moins l'infini. Vrai.
C. Pour tout réel x, f '(x) = (1-x) e^1-x. Vrai.
On pose u = x et v =e^1-x ; u'=1 et v' = -e^1-x ;
u'v +v'u = e^1-x -xe^1-x .
D. Il existe une tangente T à C qui est parallèle à la droite d. Vrai.
Coefficient directeur de T : (1-x) e^1-x ; pour x = 0 ce coefficient vaut e.
E. C est en dessous de la droite D sur ]−∞, 0[. Vrai.
sur ]−∞, 0[, xe^1−x est inférieur à e x +15 .

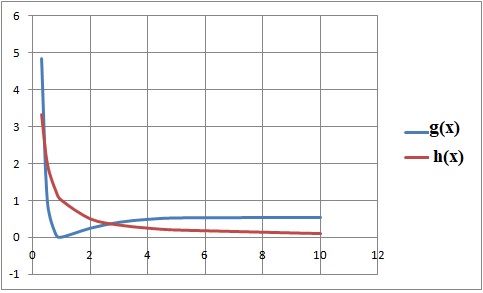
5. Soit g la fonction définie sur ]0,+∞[ par g(x) =(ln(x))² / x, représentée par la courbe C dans un repère orthonormal.
Soit h la fonction définie sur ]0,+∞[ par h(x) =1 /x, représentée par la courbe C′.
A. La limite en zéro de g(x) est égale à zéro. Faux.
(ln(x))² tend vers plus l'infini quand x tend vers zéro.
B. Pour tout réel x strictement positif, g′(x) =[2 ln(x) -(ln(x))²] / x². Vrai.
On pose u =( ln(x))² et v = x ; u' = 2 ln(x) / x ; v' = 1.
(u'v-v'u) / v² = (2ln(x) -( ln(x))² ) / x² .
C. Pour tout réel x strictement positif, g(x) /2 =[ln(x^½) / x^½]². Faux.
[ln(x^½) / x^½]² =[ ln(x^½)]² / x = [0,5 ln(x)]² /x.
D. C admet une asymptote parallèle à l’axe des abscisses. Vrai.
E. C est au-dessus de C′ sur ]1 /e ; +oo[ . Faux.
(ln(x))² / x -1/x =[(ln(x))² -1] / x > 0 si x appartient à ]1 /e ; +oo[

...

2018.
Exercice 3. Fonction.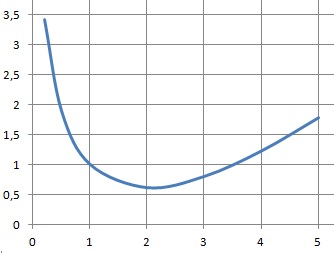
Soit f la fonction dérivable sur ]0 ; +oo[ définie par f(x) = x-ln(x²). On donne ln(2) ~0,69.
A Quand x tend vers zéro par valeur positive, f(x) tend vers plus l'infini. Vrai.
ln(x²) tend vers moins l'infini et -ln(x²) tend vers plus l'infini.
B Quand x tend vers plus l'infini, f(x) tend vers plus l'infini. Vrai.
C f(x) est croissante sur ]0 ; +oo[ Faux.
On pose u = x² ; dérivée de ln(u) = u' / u = 2x / x² = 2 /x ; f '(x) = 1 -2 / x ;
f '(x) s'annule pour x = 2 ; f '(x) est positive si x >2 et négative si x < 2.
f(x) est décroissante sur ]0 ; 2 [ et croissante sur ]2 ; + oo[.
D f '(1) = 0. Faux.
f '(1) = 1-2 = -1.
E Pour tout x de ]0 ; 2[, f(x) est positive. Vrai.
f(x) décroît de plus l'infini à f(2) = 2-ln(4) = 2-2 ln(2) ~2(1-0,69)=0,62, puis croît de0,62 à plus l'infini.

Exercice 4. Fonction.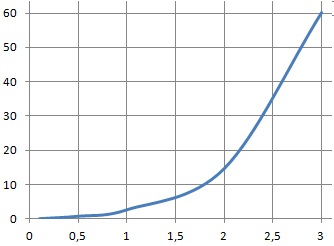
Soit f la fonction dérivable sur ]0 ; +oo[ définie par f(x) = exp(x+ln(x)).
A f(1) = e. Vrai.
f(1) = exp(1 +ln(1) = exp(1+0) = e.
B Pour tout x de ]0 ; +oo[ , f(x) = e^x+x. Faux.
f(x) = exp(x) * exp(ln(x)) = e^x x.
C f(x) est croissante sur ]0 ; +oo[. Vrai.
On pose u = e^x et v = x ; u' = e^x ; v' = 1 ; u'v +v'u = e^x(x+1) >0.
D Pour tout x de ]0 ; +oo[, f '(x) = e^x(x+1). Vrai.
E Quand x tend vers zéro par valeuur positive, f(x) tend vers 1.. Faux.
e^x tend vers 1 et x tend vers zéro ; xe^x tend vers zéro.

Exercice 5. Fonction.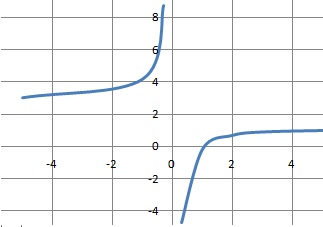
Soit f la fonction dérivable sur R-{0} définie par f(x) = (e^x-3) / (e^x-1).
A Quand x tend vers plus l'infini, f(x) tend vers 1. Vrai.
Mettre e^x en facteur au numérateur et au dénominateur puis simplifier.
f(x) = (1-3 / e^x) / (1-1/e^x) ; 1/e^x tend vers zéro et f(x) tend vers 1. Faux.
B Quand x tend vers moins l'infini, f(x) tend vers 1.
Quand x tend vers moins l'infini e^x tend vers zéro et f(x) tend vers 3.
C Quand x tend vers zéro par valeur positive, f(x) tend vers moins l'infini. Vrai.
e^x tend vers 1 ; (e^x-3) tend vers -3 ; (e^x-1) tend vers 0 par valeur positive ; f(x) tend vers moins l'infini.
D f '(x) = 2 /(e^x-1)². Faux.
On pose u = e^x-3 et v = e^x-1 ; u' = e^x ; v' = e^x ; (u'v-v'u) / v² =e^x( e^x-1-e^x+3) / (e^x-1)² = 2e^x /(e^x-1)².
E f est croissante sur ]0 ; +oo[. Vrai.
Sur ]0 ; +oo[, f '(x) est positive.

....

2017.
2. Pout tout x réel.
A. e^x+2 = e^x +e². Faux.
e^x+2 = e^x fois e².
B. e^2x-2e^x+1 >0. Vrai.
On pose X = e^x ; X²-2X+1 = (X-1)² >0.
C. racine carrée (e^x)=e^0,5x. Vrai.
racine carrée (e^x) = (e^x)^0,5.
D. Si x >0, exp (x ln(x)) = x^x. Vrai.
exp (xln(x))=exp( ln(x^x).
E. Si x <0, e^1-x -e^-x <0. Faux.
On pose u = -x >0 ; e^1+u -e^u >0.

3. Soit f la fonction dérivable sur ]0 ;+oo[ définie par f(x) = x ln(x)-x.
A. Quand x tend vers 0⁺, la limite de f(x) est égale à zéro. Vrai.
Quand x tend vers 0⁺ : ln(x) tend vers moins l'infini ; ln(x)-1 tend vers moins l'infini.
x(ln(x) -1) tend vers zéro.
B. Quand x tend vers plus l'infini, la limite de f(x) est égale à zéro. Faux.
Quand x tend vers +oo : ln(x) tend vers plus l'infini ; ln(x)-1 tend vers plus l'infini.
x(ln(x) -1) tend vers plus l'infini.
C. Pour tout x appartenant à ]0 ; +oo[, f '(x) = ln(x). Vrai.
On pose u = x ; v = ln(x)-1 ; u' = 1 ; v' = 1/x.
u'v +v'u = ln(x)-1 +1.
D. f est croissante sur ]0 ; +oo[. Faux.
f '(x) est négative si x appartient à ]0 ; 1[ et positive si x >1.
f(x) strictement décroissante sur ]0 ; 1[ et croissante si x >1.
f(x) présente un minimum égal à -1 pour x = 1
E. Pour tout x appartenant à ]0 ; +oo[, f(x) > 0. Faux.

4 Soit f la fonction dérivable sur R définie par f(x) = x-e^-x.
A. f est strictement croissante sur R. Vrai.
f '(x) = 1 +e^-x >0.
B. f(1) >0. Vrai.
f(1) = 1 -1/e ~1-1 /2,7 ~0,63.
C. Il existe x appartenant à ]0 ; 1 [ tel que f(x)=0. Vrai.
f(0) = -1 ; f(1) >0 ; f(x) est strictement croissante.
D. Pour tou x réel, f(x) est négative ou nulle. Faux..
E. Pour tou x réel, f '(x) <1. Faux.

2016.
2. Soient deux fonctions définies sur R par f(x) = 1-4e^x / (e^2x+1) et g(x) = e^2x-1.
A. Pour tout x appartenant à ]-oo ; 0], g(x) est négatif ou nul. Vrai.
1 / e^-2x est inférieur ou égal à 1 sur ]-oo ; 0].
B. Pour tout x appartenant à [0 ; +oo[, f '(x) est positif ou nul. Vrai.
On pose u = e^x et v = e^2x+1 ;u' = e^x ; v' = 2e^2x.
(u'v -v'u) / v² = (e^x(e^2x+1) - 2e^xe^2x ) / (e^2x+1)² = e^x (1-e^2x) / (e^2x+1)²
f '(x) = 4e^x (e^2x-1) / (e^2x+1)² .
C. f(x) est décroissante sur ]-oo ; 0]. Vrai.
La dérivée f '(x) est du signe de e^2x-1.
1 / e^-2x est inférieur ou égal à 1 sur ]-oo ; 0] ;
f '(x) est donc négative et f(x) est décroissante sur ]-oo ; 0].
D. La limite de f(x) est égale à 1 lorsque x tend vers moins l'infini. Vrai .
Au voisinage de moins l'infini, le terme en exponentielle tend vers zéro.
E. La limite de f(x) est égale à 1 lorsque x tend vers plus l'infini. Vrai .
Par croissance comparée e^x / (e^2x+1) tend vers zéro lorsque x tend vers l'infini.

4. Soit f la fonction numérique définie sur [1 ; +oo[ par f(x) = ln(2x) +1-x.
A. f(1) >0. Vrai.
f(1) = ln(2)+1-1 = ln(2).
B. Pour tout x appartenant à [1 ; +oo[, f '(x) = (1-x) / x. Vrai.
f '(x) = 2 /(2x) -1 = (1-x) / x.
C. f(x) est strictement décroissante sur [1 ; +oo [. Vrai.
f '(x) est négative sur ]1 ;+ oo [ ; f (x) est strictement décroissante sur ]1 ;+ oo [
D. La limite de f(x) est égale à -oo quand x tend vers plus l'infini. Vrai.
Par croissance comparée, x croît plus vite que ln(2x) quand x tend vers l'infini.
E. Il existe un unique réel a appartenant à [1 ; +oo [, a = ln(2a) +1. Vrai.

menu