Physique,
concours Orthoptie Paris Descartes 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Exercice VI. Guitare classique ou guitare folk.
Pour chaque guitare, le son est enregistré par un microphone à l'aide d'une interface d'acquisition.
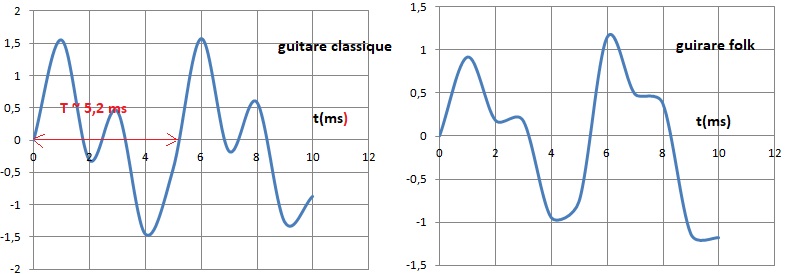
Guitare classique : fondamental f0 = 192 Hz, première harmonique f1 = 394 Hz.
Guitare folk : fondamental f0 = 192 Hz, harmoniques f1 = 394 Hz ; f2 = 576 Hz ; f3 = 768 Hz et f4 = 960 Hz.
Un sonomètre a permis de mesurer le niveau sonore des deux guitares placées à un mètre de celui-ci. L1 = 59 dB pour la guitare classique et L2 = 52 dB pour la guitare folk.
1.a Evaluer le caractère pur ou complexe des deux sons enregistrés.
1.b Quelle est la conséquence sur les spectres en fréquence.
Le
signal temporel d'un son pur est sinusoïdal et son spectre en fréquence
comporte une seule raie. Les sons sont donc complexes, présence d'une
ou plusieurs harmoniques.
2. Calculer la période et la fréquence du son émis.
Fréquence du fondamental f0 = 192 Hz ; période T = 1 / 192 =5,2 10-3 s.
3. Quel caractère physiologique commun possèdent les deux sons.
Les deux sons ont la même hauteur ( même fréquence du fondamental)..
4. Qu'est qui différencie les signaux temporels ? Quel caractère physiologique du son cela met-il en évidence ?
Les deux sons ne possèdent pas le même nombre d'harmoniques : ils n'ont pas le même timbre.
Le son émis par la guitare folk est plus riche en harmoniques.
5. Donner
l'expression du niveau sonore d'une source sonore d'intensité I.
Calculer les intensités sonores correspondant aux niveaux L1 et L2.
L = 10 log ( I / I0) avec L en dB et I en W m-2.
I = I0 100,1 L ;
I1 = 10-12 x 105,9 =10-6,1 = 7,94 10-7 W m-2.
I2 = 10-12 x 105,2 =10-6,8 = 1,58 10-7 W m-2.
6. Si les deux guitares jouent en même temps et dans les mêmes conditions, quel aurait été le niveau sonore ?
Itotal = I1 + I2 = 9,52 10-7 W m-2.
L = 10 log ( 9,52 10-7 / 10-12) =59,8 dB.
Exercice VII. Le lanceur Ariane.
texte : le premier lanceur Ariane est une fusée )
trois étages dont la hauteur totale est de 47,4 m et qui pèse, avec sa
charge utile (satellite), 208 tonnes au décollage. Le premier étage,
qui fonctionne pendand 145 s est équipé de 4 moteurs Viking V alimentés
par du peroxyde d'azote N 2O 4 ( masse de peroxyde
emportée 147 tonnes). L'intensité de la force de poussée totale F de
ces 4 moteurs est constante pendant leur fonctionnement : elle vaut F=
2445 kN.
Le lanceur peut mettre en orbite circulaire basse de 200 km
d'altitude un satellite de 4850 kg. Il peut également placer en orbite
géostationnaire un satellite de 965 kg. Il peut être aussi utilisé pour
placer en orbite héliosynchrone des satellites très utiles pour les
applications météorologiques.
- L'ascension de la fusée Ariane :
Le champ de pesanteur est supposé uniforme : g0 = 9,8 m/s².
On choisit un axe Oz vertical vers le haut. On étudie le mouvement de
la fusée dans le référentiel terrestre supposé galiléen
a- Représenter sur un schéma en les nommant les deux forces qui
agissent sur la fusée Ariane lorsqu'elle s'élève verticalement. On
néglige les frottements et la poussée d'Archimède
b- A un instant quelconque, la masse de la fusée est m. Déterminer en
fonction de m et des intensités des deux forces précédentes la valeur
de l'accélération a.
c- On considère d'abord la situation au décollage. La masse de la fusée
vaut alors m1. Calculer la valeur numérique de
l'accélération a à cet instant. On envisage la situation qui est celle
immédiatement avant que tout le peroxyde d'azote ne soit consommé. La
masse de la fusée vaut alors m2 . Calculer la valeur
numérique de m2 puis celle de l'accélération a2 à
cet instant. Le mouvement de la fusée est-il uniformément accéléré ?
d- La vitesse d'éjection Ve des gaz issus de la combustion
du peroxyde d'azote est donnée par la relation : ( les vecteurs sont
écrits en bleu et en gras) Ve
= Dt / D m F. où Dt / D m est la variation de la masse de la fusée par
unité de temps et caractérise la consommation des moteurs. Vérifier
l'unité de Ve par analyse dimensionnelle. Calculer la valeur
numérique de Ve. Quel est le signe de Dt
/ D m ? En déduire le sens de Ve.
Qu'en pensez vous ?
A l'aide d'une loi connue que l'on énoncera, expliquer pourquoi
l'éjection des gaz propulse la fusée vers le haut.
Corrigé.
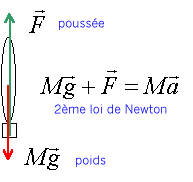
sur un axe Oz
vertical vers le haut : F-Mg=Ma
a = F/M -g0.
a1 = 2,445 106 / 2,08 105
-9,81 = 1,94 m/s².
m2 = 208-147,5 = 60,5 t = 6,05 104 kg
a2 = 2,445 106 / 6,05 104
-9,81 = 30,6 m/s².
l'accélération n'est pas constante : le mouvement n'est pas
uniformément accéléré.
Ve
= Dt / D m F.
force = masse * accélération ; force : [kg] [L][T]-2
;
Dt / D m
F : [T] [kg] -1
[kg] [L][T]-2 = [L][T]-1 ( mètre / seconde)
consommation des moteurs : 1,475 105 / 145 = 1017,5
kg/s
Dt / D m
= 1/1017,5 = 9,38 10-4s/kg.
Ve = 9,38 10-4* 2,445 106 = 2403 m/s.
D m est négatif, car la masse de
la fusée diminue ; Dt positif ;
Ve et F colinéaires mais de sens contraire ; F est dirigée vers le haut ; Ve est dirigée vers le bas.
principe des actions mutuelles ( 3 ème loi
de Newton) ou principe de l'action et de la réaction :
Si un corps A (fusée) exerce sur un corps B ( gaz éjectés) une
force FA-->B ,
inversement B exerce sur A une action opposée FB-->A
= - FA-->B
Propulsion par réaction.
|
|
|
Exercice VIII.
Lors
d’un match de football, un joueur doit tirer un penalty et décide de
tenter une « Panenka ». Le joueur dépose le ballon au point de penalty
O, pris comme origine du repère. Le joueur frappe le ballon en
direction du centre du but et lui communique une vitesse initiale �v0 de valeur 11,5 m/s
et dont la direction fait un angle a = 55° avec l’horizontale.
Données : intensité de la pesanteur : g = 9,81 N.kg-1; masse du ballon : m = 620 g ;· termes utilisés dans la pratique du football :
Les buts sont constitués de deux montants verticaux (poteaux) reliés en leur sommet par une
barre transversale. Le bord inférieur de la barre transversale se situe à une hauteur de 2,44 m par
rapport au sol.
Le penalty est une action consistant à frapper directement au but depuis un point nommé « point
de penalty » ou « point de réparation ». Un penalty est réussi si le ballon franchit la ligne de buts
en passant entre les montants et sous la barre transversale.
À l’intérieur de chaque surface de réparation, le point de penalty est marqué à 11,0 m du milieu de
la ligne de but et à égale distance des montants verticaux du but.
Schématisation du problème.
Tracer un repère orthonormé (Ox ; Oz) et représenter, dans ce repère,
la situation du penalty, sans souci d’échelle. Les grandeurs suivantes
devront apparaitre : le vecteur vitesse initiale �v0�, l’angle α, la hauteur h des buts et la distance d du point de pénalty à la ligne de but.
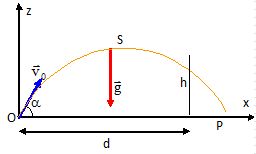
On note A le point où se situe le ballon lorsqu’il franchit la ligne de but. Quelles conditions
doivent vérifier les coordonnées (xA ; zA) de ce point pour que le pénalty soit réussi ?
xA = d = 11,0 m ; 0 < zA < h ; 0< zA < 2,44 m.
Étude dynamique du mouvement du ballon.
Dans cette partie, on étudie le mouvement du centre d’inertie G du ballon en négligeant les forces
de frottement de l’air sur le ballon ainsi que la poussée d’Archimède.
Établir l’expression du vecteur accélération �a��� du centre d’inertie
du ballon. Établir les équations horaires x(t) et z(t) du mouvement du
centre d’inertie G et montrer que l’équation de la trajectoire du
ballon, dans le plan (xOz), peut s’écrire :
z =-½gx2 /( v0 cosa)2 + x tan a.
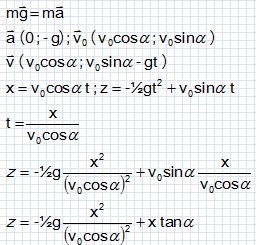 En exploitant les données et les documents, déterminer si le penalty décrit en début d’exercice
est réussi. Expliciter votre raisonnement.
Valeur de z pour x = 11,0 m :
z = -4,9 *11,02 /(11,5 *cos 55)2 +11,0 tan 55 = -13,64+15,71 ~2,1 m
Cette valeur étant inférieure à 2,44 m, le pénalty est réussi
Étude énergétique du mouvement du ballon.
On admet que le ballon passe au niveau de la ligne de but à une hauteur zA = hA.
Rappeler les expressions de l’énergie cinétique Ec, de l’énergie potentielle de pesanteur Epp et de l’énergie mécanique Em. On choisira un axe vertical ascendant et une énergie potentielle de pesanteur nulle à l’origine.
Ec = ½mv2 ; Epp = mgz ; Em = ½mv2 +mgz.
En explicitant votre
raisonnement, associer à chaque courbe la forme d’énergie
correspondante. Déterminer les valeurs de la hauteur hA et de la vitesse vA lorsque le
ballon franchit la ligne de but.
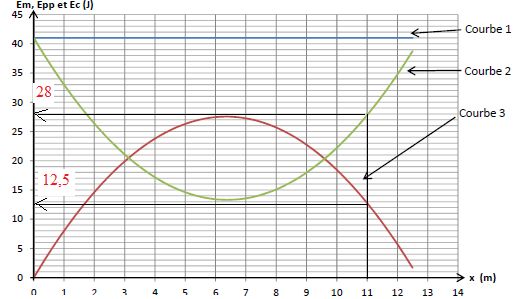
Courbe 1 : l'énergie mécanique se conserve en absence de frottement.
Courbe 2 : l'énergie cinétique initiale est maximale puis décroît jusqu'au sommet de la parabole.
Courbe 3 : l'énergie potentielle initiale est nulle puis croît jusqu'au sommet de la parabole.
Energie potentielle au point A : mghA = 12,5 ; hA =12,5 / (0,620 *9,81) =2,055 ~2,1 m.
Energie cinétique au point A : 28 = ½mv2A ; vA = (28*2 / 0,620)½ =9,5 m/s.
Que peut-on dire de l’énergie mécanique du ballon
lors de son mouvement ? Utiliser cette caractéristique du mouvement
pour retrouver la valeur vA de la vitesse du ballon lorsqu’il franchit la ligne de but. Conclure.
Lors d'une chute libre (absence de frottement ), l'énergie mécanique du ballon se conserve.
Energie mécanique initiale = énergie mécanique en A = 41 J.
½mv20 = ½mv2A +mghA ; v2A = v20 +2ghA ;
v2A =11,52 - 2*9,81 *2,055 =91,93 ; vA = 9,5 m/s.
On retrouve la valeur précédente : l'énergie mécanique du ballon est bien conservée.
A partir des courbes, déterminer la vitesse vC du ballon au point C d'abscisse 4 m. Montrer que l'altitude du point C vaut zC=3,9 m.
Exprimer la vitesse du point C en fonction de v0, m, g et zC. Calculer vC.
EC = 17 J ; vC = (2EC / m)½=(34 /0,62)½=7,4 m /s.
Ep = 24 J. zC = EP /(mg) = 24 /(0,62 x9,8) =3,95 m.
½mv20 = ½mv2C +mgzC ; v2C = v20 +2gzC ;
v2C =11,52 - 2*9,81 *3,95 =54,75 ; vC = 7,4 m/s.
|
|
|
|
Exercice IX. En panne d'essence.
Antoine pousse son véhicule en ligne droite sur une route
horizontale. Il exerce une force motrice F = 223 N. La force de
frottement f, supposée constante vaut f = 220 N. Masse de la voiture M
= 1,00 103 kg.
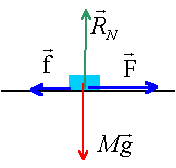
a. Faire le bilan des forces extérieures s'exerçant sur la voiture et les représenter.
La voiture est soumise à son poids, à l'action du plan, opposée au poids, à la force F et aux frottements f.
b. Quel est le référentiel le plus adapté pour l'étude du mouvement de la voiture ?
Le référentiel terrestre.
c. Ecrire l'expression vectorielle de la seconde loi de Newton.
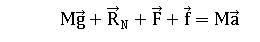
d. Montrer que la coordonnée suivant l'axe horizontal de l'accélération du véhicule est ax = 3 10-3 m s-2.
F -f = Max ; ax = (F-f) / M =(223-220) / 1000 = 3,00 10-3 m s-2.
e. L'expression de la vitesse du véhicule en fonction du temps est-elle : v =cste ; v = axt ?
L'expression horaire de la position est-elle x= Cste ; x = ½axt2 ?
La vitesse est une primitive de l'accélération et la vitesse initiale est nulle : v = axt.
La position est une primitive de la vitesse et la position initiale est l'origine de l'axe :x = ½axt2 .
f. Combien de temps faut-il pour parcourir 0,50 km ?
t =(2x / ax)½ =(2 x 500 / (3 10-3))½~5,8 102 s.
L'accident.
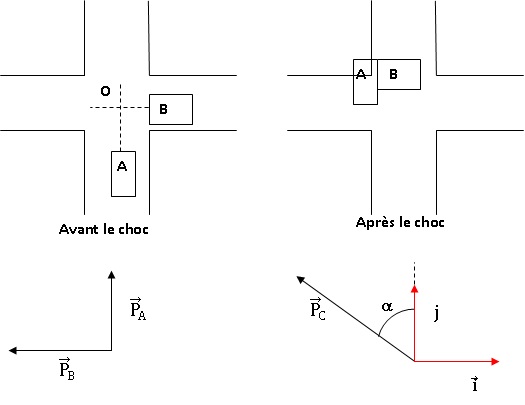
Le choc a lieu en O.
L'expert dispose des informations suivantes : vA = 45 km /h ; vB = 50 km / h.
MA = 1840 kg ; MB = 1800 kg. Sol glissant.
L'expert met en doute la vitesse déclarée par le conducteur B. Le
système étudié {voiture A + voiture B} est supposé pseudo-isolé.
1. Le mouvement est étudié dans le référentiel terrestre supposé galiléen. Que signifie référentiel galiléen ?
référentiel galiléen : dans ce référentiel le principe d'inertie ou 1ère loi de Newton s'applique " un point matériel pseudo-isolé demeure dans son état de repos ou de mouvement rectiligne uniforme".
2. En utilisant la
seconde loi de Newton, montrer que la quantité de mouvement reste
constante avant et après le choc. En déduire une relation entre les
vecteurs quantité de mouvement.
La somme des forces extérieures qui s'applique sur le système pseudo-isolé est nulle.
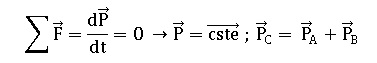
3. Déterminer les valeurs de PA et PB
des quantités de mouvement des deux voitures avant le choc. En déduire
les coordonnées du vecteur quantité de mouvement du système après le
choc.
PA = MA vA = 1840 x 45 / 3,6 = 2,3 104 kg m s-1.
PB = MB vB = 1800 x 50 / 3,6 = 2,5 104 kg m s-1.
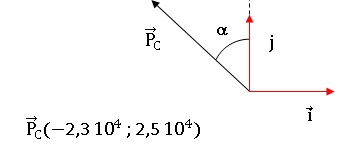
4. Déterminer la valeur de PC et de l'angle a.
Comparer a à l'angle de la direction indiquée sur le croquis. L'expert
a t-il raison de douter de la valeur de la vitesse déclarée par B
?
Pc = (PA2 +PB2)½ =(2,32 +2,52)½ 104 = 3,397 104 ~3,4 104 kg m s-1.
tan a =PA / PB = 2,3 / 2,5 = 0,92 ; a ~42,6 °.
Sur le croquis, a est plus proche de 60° que de 42 °. La vitesse de B est donc bien supérieure à la valeur 50 km/h déclarée.
.
|
|
|