Physique,
concours Orthoptie Paris Descartes 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Exercice I. Ultrasons.
On trouve dans le commerce des appareils de nettoyage utilisant des ultrasons. ( fréquence des ultrasons f = 42 kHz ± 2%)
On visualise le signal émis par l'émetteur E. On obtient le signal suivant.
Déterminer la période T du signal, puis sa fréquence.

T = 2,4 10-5 s ; f = 1 / T = 1 /(2,4 10-5) = 4,17 104 Hz ~42 kHz.
La fréquence donnée précédemment est comprise entre 41,16 kHz et 42,84 kHz.
La valeur déterminée graphiquement est donc en accord.
Exercice II. Météosat.
Les trois canaux de Météosat.
Le
radiomètre** des satellites Météosat comprend trois canaux de
télédétection : le canal C dans le visible et le proche infrarouge, le
canal E dans l’infrarouge moyen et le canal D dans l’infrarouge
thermique.
**
Un radiomètre est un appareil de mesure de l’intensité du flux de
rayonnement électromagnétique dans différents domaines de longueur
d’onde.
Canal
|
Gamme de longueurs d'onde en µm
|
Fonction principale
|
C
|
entre 0,4 et 1,1
|
Permet l'observation visuelle de la surface de la Terre et des nuages.
|
E
|
entre 5,7 et 7,1
|
Renseigne sur la teneur en humidité de l'atmosphère. La surface du sol n'est pas visible.
|
D
|
entre 10,5 et 12,5
|
Renseigne sur la température des nuages et de la surface terrestre.
|
Pourquoi
seule la télédétection sur les canaux C et D permet-elle d’obtenir des
informations en provenance de la surface terrestre ?
Courbe de transmission des radiations électromagnétiques par
l’atmosphère terrestre en fonction de la longueur d’onde l.
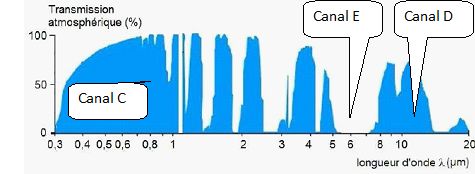
Les gammes des longueurs d'onde du canal E ne sont pas transmises par l'atmosphère. Celles des caneaux C et D le sont.
Quelles
sont les raisons qui ont guidé le choix de la gamme de longueurs d’onde
du canal D, compte tenu de sa fonction principale ?
Le canal D nous renseigne sur la température des nuages et du sol.
Loi de Wien : lmax
T = 2,90 x 103 μm.K
T = 2,90 x 103 /10,5 =276 K ou 3 °C.
T = 2,90 x 103 /12,5 =232 K ou -41 °C.
Cet intervalle de température correspond bien à celle des nuages, mais pas à la température du sol terrestre.
|
|
|
Exercice III.
Comment les ondes sismiques se
propagent-elles ?
Quand la Terre tremble, les vibrations se propagent dans
toutes les directions à partir du foyer du tremblement de terre situé
dans les profondeurs de la couche terrestre. Les vibrations sont
initialement de deux types : celles qui compriment et détendent
alternativement les roches, à la manière d'un accordéon, et celles plus
destructrices qui les cisaillent. Les premières, les plus rapides
(appelées ondes P), voyagent dans la croûte à une vitesse de 6 km/s
environ, mais peuvent être ralenties dans les roches peu consolidées.
Les secondes (appelées ondes S) sont, à cause des propriétés élastiques
des roches, systématiquement deux fois plus lentes mais environ cinq
fois plus fortes que les premières. Ainsi, lors d'un séisme lointain,
ayant ressenti l'onde P, on peut anticiper l'arrivée des ondes S.
Peut-on les distinguer quand un séisme a lieu sous nos pieds ?

|
Oui : les ondes P vibrent dans leur direction de
propagation, elles soulèvent ou affaissent le sol, tandis que les ondes
S vibrent perpendiculairement et nous secouent horizontalement.
|
Heureusement, lors de leur voyage à travers le sous-sol, les ondes
perdent de leur énergie. En s'éloignant du foyer, elles s'amortissent
et leurs effets s'atténuent. Voilà pourquoi les séismes superficiels,
trop proches pour être affaiblis, sont les plus destructeurs.
D'après La Recherche (n° exceptionnel août octobre 2001 LES
SEISMES)
Ondes mécaniques :
- Les ondes sismiques appartiennent au domaine des ondes
mécaniques. Donner la définition générale d'une onde mécanique.
- Dans le texte, on peut lire : "les premières voyagent dans
la croûte à une vitesse de 6 km/s environ". Quel terme plus approprié
que "vitesse" devrait-on utiliser ?
- Les ondes sismiques peuvent être, selon les cas, qualifiées
par les termes suivants : ondes longitudinales ; ondes de cisaillement
; ondes transversales ; ondes de compression.
- En utilisant deux termes de la liste ci-dessus, caractériser une onde
P. Justifier la réponse.
- En utilisant deux termes de la liste ci-dessus, caractériser une onde
S. Justifier la réponse.
- Associer chacun des deux schémas ci-dessous aux ondes P ou S.
Justifier la réponse.
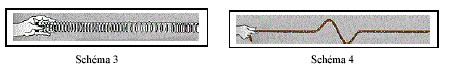
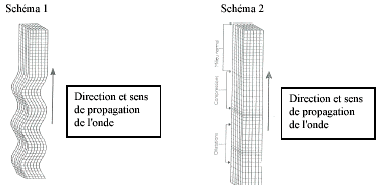
- Les expériences ci-dessous peuvent modéliser les ondes P ou
S. Associer chaque expérience à l'un des deux types d'onde.
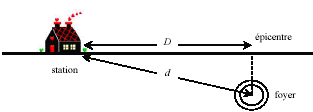
- Épicentre et foyer du séisme
- Une onde sismique commence à se propager à partir du foyer à la date t
= 0. Une station enregistreuse est située à une distance D de
l'épicentre et à une distance d du foyer. On note Vp la célérité de
l'onde P et Vs la célérité de l'onde S dans la croûte. Donner
l'expression de tp et tS, dates d'arrivée
respectivement des ondes P et S à la station enregistreuse
- On ne peut pas connaître précisément Vp et VS.
Cependant, on sait qu'elles obéissent à la relation :
1/VS -1/Vp = 1/8 avecVS et VP
étant exprimées en km.s-1. Si on mesure les dates tS
et tP, établir l'expression de la distance d en fonction de
ces dates.
- Un capteur de la station mesure l'intervalle de temps séparant
l'arrivée des deux ondes à la station : Dt.
= 25 s. En déduire la distance de la station au foyer du séisme.
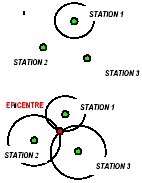
- On appelle foyer superficiel un foyer très proche de la surface
terrestre. Dans ce cas, on peut considérer que d = D. Une des méthodes
utilisées pour localiser l'épicentre du séisme dans ce cas est la
méthode dite des trois cercles : trois stations S1, S2
et S3 mesurent la distance à laquelle elles se trouvent du
foyer d'un séisme. On note des distances respectivement d1, d2
et d3. On suppose que le milieu est isotrope, c'est à dire
que les ondes se propagent à la même vitesse dans toutes les
directions. Expliquer le principe de la méthode dite « des trois
cercles ».
corrigé
On appelle onde mécanique le phénomène de
propagation d'une perturbation dans tout milieu matériel sans transport
de matière.
On devrait
utiliser le terme de célérité d'une onde.
Les ondes P (schéma
1 ) sont des ondes longitudinales : la direction de déplacement
temporaire de la matière et la direction de propagation de l'onde sont les
mêmes. On parle aussi d'ondes de compression : elles créent de proche
en en proche des ondes de compression-détente du milieu de propagation.
Les ondes S
sont des ondes transversales : la direction de déplacement temporaire
de la matière et la direction de
propagation de
l'onde sont perpendiculaires. On parle aussi d'ondes de cisaillement.
Si les ondes S et
P se propagent dans un milieu supposé non dispersif, la perturbation au point M' (station
enregistreuse) à
l'instant t' est
la même que celle qui existait au point M (foyer) à l'instant t= t'- t, avec t =MM'
/ V , t étant le retard et V la
célérité de
l'onde considérée. Donc,
en prenant l'origine des temps t = 0 à l'instant où le séisme démarre :
tP=d/Vp ; tS=d/VS ;
Dt =tS- tP=d
(1/VS -1/VP )=d/8
d = 8Dt = 8*25 = 200 km.
|
A
partir de la position de la station 1, on trace un cercle dont le
rayon d1
correspond à peu près à la distance épicentrale D1. On fait
de même pour les stations 2 et 3. Les arcs de cercle se coupent en un seul point si le
séisme est superficiel. Le point d'intersection donne la position de
l'épicentre.
|
|
|
|
|
Exercice IV. Doppler.
L'ambulance munie d'une sirène se déplace vers la droite à la vitesse v. La sirène émet un son de fréquence f = 680 Hz.
Le véhicule se rapproche d'un observateur immobile.
Pendant l'intervalle de temps T, le son parcourt la distance l. Pendant ce temps, le véhicule parcourt la distance d = v T.
La longueur d'onde l' perçue par l'observateur à droite de la source a pour expression : l' = l-vT.
1.1. Rappeler la relation liant la vitesse de propagation, la longueur d'onde et la fréquence.
l =cT = c / f.
1.2. En déduire la relation : f ' = f c / (c-v), f ' étant la fréquence perçue par l'observateur.
l' = l-vT = c / f - v / f = (c-v) / f.
D'autre part l' = c / f ' ; d'où : c / f ' = (c-v) / f ; soit : f ' = f c / (c-v).
1.3. Le son perçu est-il plus aigu ou plus grave ?
c / (c-v) > 1, donc f ' > f, le son est donc plus aigu.
2. Dans un deuxième temps, le véhicule s'éloigne de l'observateur à la même vitesse v.
2.1. Donner , sans démonstration, les expressions de la nouvelle longueur d'onde l" et de la nouvelle fréquence f" perçue par l'observateur.
l" = l + vT et f " = f c / (c+v).
1.3. Le son perçu est-il plus aigu ou plus grave ?
c / (c+v) < 1, donc f " < f, le son est donc plus grave.
3. Exprimer, puis calculer en km / h, la vitesse du véhicule qui se rapproche de l'observateur sachant que f ' = 716 Hz.
f ' (c-v) = f c ; c-v = f / f ' c ; v' = c( 1-f / f ').
v = 340 (1 -680 / 716) = 17,1 m /s soit 17,1 x3,6 = 61,54 ~ 62 km / h.
.
Exercice V. La lumière.
I- Première expérience
:
On place perpendiculairement au faisceau lumineux et à
quelques centimètres du laser, une fente fine et horizontale de largeur
a. Un écran situé à une distance D de la fente, montre des taches
lumineuses réparties sur une ligne verticale. La tache centrale plus
lumineuse que les autres, est la plus large.
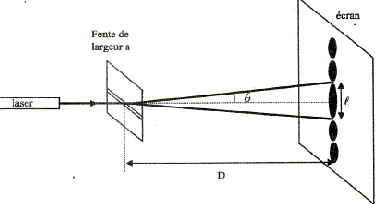
La lumière émise par le laser est diffracté
par le fente dont la largeur est du même ordre de grandeur que la
longueur d'onde l. Par analogie avec les
ondes mécaniques, cette expérience prouve le caractère ondulatoire de
la lumière.
L'angle q est donné par la
relation : q =l/a
ou demi écart angulaire correspondant à la tache centrale de
diffraction.
l et a s'expriment en mètre et q en radian.
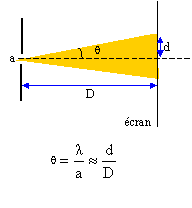
d'où d = lD/a ; en conséqence la
largeur de la tache centrale " 2d= l "
augmente lorsqu'on réduit la largeur "a" de la fente.
si l = 38 mm, l = 633 nm = 6,33 10-7 m et D = 3,00
m. la largeur a de la fente vaut : a = 2lD/l.
a = 2*6,33 10-7 *3,00 / 3,8 10-2 = 1,0 10-4 m.
|
|
Expérience 2
: interférences.
On
remplace la fente de largeur a, par deux fentes parallèles,verticales et distantes de b = 0,40 mm.
2.1. Quel phénomène observe t-on ? Schématiser la figure observée sur un écran.
Ces
deux
fentes se comportent comme deux sources S1 et S2
émettant en phase. Sur l'écran qui a été légèrement déplacé, on observe
la figure d'interférences ci-dessous.

2.2. L'interfrange est donné par la relation i = lD / b. Définir l'interfrange puis la calculer.
L'interfrage est la distance séparant deux franges consécutives de même nature.
i = 633 10-9 x 3,00 / (4 10-4) ~4,75,0 10-3 m = 4,75 mm.
2.3. Pourquoi faut-il mesurer expérimentalement six interfranges au l'ieu d'une ?
On augmente la précision sur la mesure de l'interfrange.
|
|