Mathématiques,
concours Audioprothésiste Nancy 2010.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
I ( 2 points)
Calculer la fonction dérivée de la fonction suivante : f(x) = 1 / (x4+x2+1)4.
On pose : u = x4+x2+1 ; u'=4x3 +2x.
f(u) = u-4 ; f '(u) = -4 u'u-5.
f '(x) = -4(4x3 +2x) / (x4+x2+1)5.
II (8 points)
Soit l'application f définie par : f(x) = (x2-6x+5)½.
1. Définir le domaine de définition D de la fonction f.
x2-6x+5 > 0 ; Chercher les solutions de x2-6x+5=0.
Discriminant D = (-6)2-4 x5 = 16 ; x1 = (6+4) / 2 = 5 et x2 = (6-4) / 2 = 1.
Domaine de définition : ]-oo ; 1] u [5 ; +oo[.
2. Démontrer que la droite x = 3 est axe de symétrie.
Le domaine de définition est symétrique par rapport 3.
Quelque soit h : on pose H = h+2.
f(3+H) appartient à D et f(3+H)=[(H+3)2-6(H+3)+5 ]½= (H2-4)½ .
f(3-H) appartient à D et f(3-H)=[(3-H)2-6(3-H)+5 ]½= (H2-4)½ .
f(3+H) =f(3-H) : la droite d'équation x=3 est axe de symétrie de la courbe.
f(3+h) appartient à D et f(3+h)=(h+3)2-6(h+3)+5 = h2+9+6h-6h-18+5 = h2-4.
3. Etudier le sens de variation de f sur D.
Dériver f en posant u = x2-6x+5 ; u' = 2x-6 ; f '(x) = ½u ' u-½.
f '(x) = (x-3) / (x2-6x+5)½.
Si x appartient à ]-oo ; 1], f '(x) <0 et la fonction f est strictement décroissante.
Si x appartient à [ 5 ; +oo (, f '(x) >0 et la fonction f est strictement croissante.
4. Déterminer les limites de f(x).
f(x) = (x2(1-6 / x+5 /x2))½ = |x| (1-6 / x+5 /x2)½ .
Si x tend vers plus ou moins l'infini :
6 / x+5 /x2tend vers zéro.
f(x) tend vers |x| soit plus l'infini.
Si x tend vers 1, f(x) tend vers zéro.
Si x tend vers 5, f(x) tend vers zéro.
|
|
|
5. Déterminer les équations des droites asymptotes.
Droite asymptote d'équation : y= ax +b.
Pour trouver a, on cherche la limite de f(x) / x =|x| (1-6 / x+5 /x2)½ / x.
Si x tend vers plus l'infini: f(x) / x tend vers 1.
Si x tend vers moins l'infini : f(x) / x tend vers -1.
Pour trouver b, on cherche la limite de f(x)-ax =(x2-6x+5)½ -ax.
Limite en plus l'infini : [(x2-6x+5)½ -x] [(x2-6x+5)½ +x] / [(x2-6x+5)½ +x]=(x2-6x+5-x2) / [(x2-6x+5)½ +x].
(-6x+5) / [(x2-6x+5)½ +x] = (-6 +5 /x) / (1-6 /x+5 / x2+1).
Cette expression tend vers -6/2 = -3 si x tend vers plus l'infini.
Equation de l'asymptote oblique y = x-3.
Limite en moins l'infini : [(x2-6x+5)½ +x] [(x2-6x+5)½ -x] / [(x2-6x+5)½ -x]=(x2-6x+5-x2) / [(x2-6x+5)½ -x].
(-6x+5) / [(x2-6x+5)½ -x] = (-6 +5 /x) / (|x|(1-6 /x+5 / x2)-1).
Cette expression tend vers -6 / (-2 )= +3 si x tend vers moins l'infini.
Equation de l'asymptote oblique y = -x+3.
6. Dresser le tableau de variation de f.
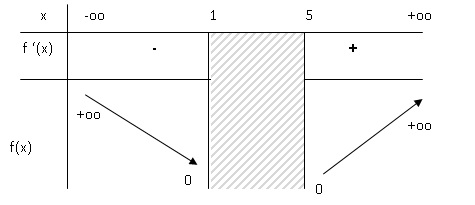
.
7. Tracer la courbe C et les asymptotes.
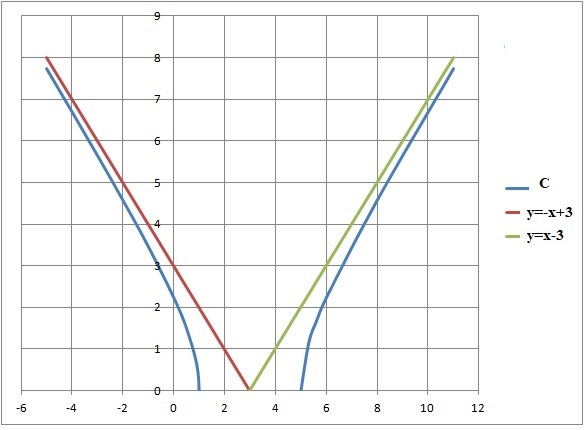
|
|
|
|
III ( 2 points )
Soit la fonction f définie sur [0 ; +oo[ par f(x) = ln(e2x+2e-x).
Montrer que pour tout réel x positif : f(x) = 2x + ln(1+2e-3x).
f(x) = ln ((e2x)(1+2e-3x)) =ln(e2x) + ln(1+2e-3x) = 2x + ln(1+2e-3x)..
IV. ( 3 points)
Calculer Les intégrales suivantes :
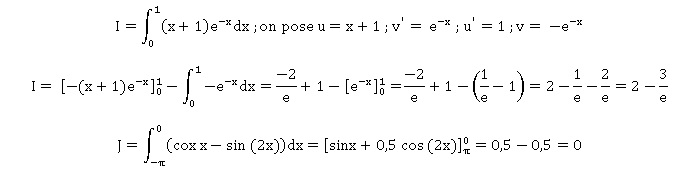
V. ( 5 points)
1. Ecrire sous forme algébrique les nombres complexes :
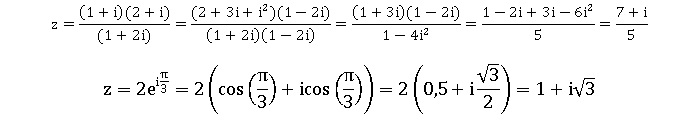
|
|
2. Ecrire sous forme trigonométriques les nombres complexes.
z = 1+i ; |z| = (12 +12)½ =2½.
z / |z| = 1 / 2½ +i /2½ = cos (p /4) + i sin(p/4) ; z = 2½(cos (p /4) + i sin(p/4)).
z = 1 +2i ; |z| = (12 +22)½ =5½.
z / |z| = 1 / 5½ +2i / 5½ = cos (63,43) + i sin(63,43) ; z = 5½(cos (63,43) + i sin(63,43)).
3. Ecrire z = 2-2i sous forme trigonométrique et en déduire la forme algébrique de z10.
|z| = (22 +(-2)2)½ =8½.
z / |z| = 2 / 8½ -2i / 8½ =1 / 2½ -i / 2½ = (cos (-p /4) + i sin(-p/4)) ;
z =8½(cos (-p /4) + i sin(-p/4)) = 8½exp(-ip/4).
z10 =85 exp(-i10p/4)=85 exp(-ip/2)=85 (cos (-p /2) + i sin(-p/2)) = -85i.
|
|