QCM mathématiques, concours Audioprothésiste Bordeaux 2018. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Question 1 La droite passant par les points A(2 ; 3) et B (-4 ; 5) a pour équation : A. y=-3x+9 B.y = -3x+3 C. y = 5 / 3 x -1/3 D. y = -1 /3 x+9 E. aucune des solutions proposées n'est correste. Vrai. y = ax+b. Le point A appartient à la droite : 3 = 2a+b; le point B appartient à la droite : 5 = -4a+b. 5-3 = -4a-2a soit a = -1 /3 et b = 11 /3. Question 2 La droite passant par les points A'(-5 ; 6) et B' (-5 ; -4) a pour équation : A. y=-x+1 B.y = -x-1 C. y = -4/5x+1 D. y = x+11 E. aucune des solutions proposées n'est correste. Vrai. Droite verticale d'équation x = -5. Question 3 Une équation paramétrique de la droite passant par les points A(-1 ; 2 ; -3) et B(1 ; 3 ; -2) est avec t réel. A. x = 1+t ; y = 3+2t ; z = -2+t. Coordonnées du vecteur directeur ( 1 ; 2 ; 1). B. x = -1+t ; y = 2-2t ; z = -3+t. Coordonnées du vecteur directeur ( 1 ; -2 ; 1) C. x = 1+2t ; y = 3+t ; z = -2+t. Coordonnées du vecteur directeur ( 2 ; 1 ; 1) D. x = -1+4t ; y = 2-2t ; z = -3+t. Coordonnées du vecteur directeur ( 4 ; -2 ; 1) E. x = 1-4t ; y = 3-2t ; z= -2+2t. Coordonnées du vecteur directeur ( -4 ; -2 ; 2) Coordonnées du vecteur AB ( 1-(-1) ; 3-2 ; -2-(-3) soit (2 ; 1 ; 1). Seule la proposition C pourrait convenir. Dans ce cas, B appartenant à la droite : 1 = 1+2t soit t =0 ; par suite yB = 3  et zB =-2. A appartenant à cette droite et t = 0 : xA =  1 ; différent de -1 ; Aucune des solutions proposées ne convient. Question 4 Une équation paramétrique de la droite passant par le point A' (2 ; -1 ; -3) et ayant un vecteur directeur de coordonnées (-6 ; 4 ; -2) est ( avec t réel) : A. x =2+6t ; y = -1+4t ; z = -3 +2t. Coordonnées du vecteur directeur de cette droite ( 6 ; 4 ; 2). B. x=-4+3t ; y = 3-2t : z  =-5+t. Vrai. Coordonnées du vecteur directeur de cette droite ( 3 ; -2 ; 1), colinéaire au vecteur de coordonnées (-6 ; 4 ; -2).. C. x=2-6t ; y = -1-4t ; z = -3-2t. Coordonnées du vecteur directeur de cette droite ( -6 ; -4 ; -2). D. x=2+3t ; y = -1+2t ; z = -3+t. Coordonnées du vecteur directeur de cette droite ( 3 ; 2 ; 1). E. x = -4+3t ; y = 3+2t ; z = -5+t. Coordonnées du vecteur directeur de cette droite ( 3 ; 2 ; 1). Seule la proposition B pourrait convenir. A' appartenant à la droite : 2 = -4+3t soit t = 2 ; par suite yA' = 3-4 = -1 et zA' = -5+2=-3. On considère le plan P d'équation 2x-y+3z+5=0. Question 5 La droite d'équation paramétrique x = 2-t ; y = -1+t ; z = 3+t avec t réel : A. est parallèle au plan P, non contenue dans P. Vrai. B. est perpendiculaire au plan P. C. est contenue dans P. D. est sécante et non perpendiculaire au plan P. E. aucune des solutions proposées ci-dessus n'est correcte. Coordonnées du vecteur directeur de la droite : ( -1 ; 1 ; 1). Coordonnées d'un vecteur perpendiculaire au plan P : (2 ; -1 ; 3). La droite n'est pas perpendiculaire au plan P. Si la droite et le plan sont sécants : 2(2-t)-(-1+t)+3(3+t)+5=0 ; 19+0t = 0, impossible. La droite et le plan ne se coupent pas. Le plan et la droite ne sont pas confondus, car quel que soit t : 2(2-t)-(-1+t)+3(3+t)+5 diffère de zéro.  La droite et le plan sont donc parallèles. Question 6 La droite d'équation paramétrique x = 1+4t ; y = 2-2t ; z=5+6t avec t réel : A. est parallèle au plan P, non contenue dans P. B. est perpendiculaire au plan P. Vrai. C. est contenue dans P. D. est sécante et non perpendiculaire au plan P. E. aucune des solutions proposées ci-dessus n'est correcte. Coordonnées du vecteur directeur de la droite : ( 4 ; -2 ; 6). Coordonnées d'un vecteur perpendiculaire au plan P : (2 ; -1 ; 3)  soit encore (4 ; -2 ; 6).  La droite est  perpendiculaire au plan P. Question 7 La droite d'équation paramétrique x = 2+2t ; y = 2-t ; z = 1-t avec t réel : A. est parallèle au plan P, non contenue dans P. B. est perpendiculaire au plan P. C. est contenue dans P. D. est sécante et non perpendiculaire au plan P. Vrai. E. aucune des solutions proposées ci-dessus n'est correcte. Coordonnées du vecteur directeur de la droite : ( 2 ; -1 ; -1). Coordonnées d'un vecteur perpendiculaire au plan P : (2 ; -1 ; 3). La droite n'est pas perpendiculaire au plan P. Si la droite et le plan sont sécants : 2(2+2t)-(2-t)+3(1-t)+5=0 ; 10+2t = 0, soit t = -5 La droite et le plan se coupent. On considère, pour tout entier naturel n, la suite (un) définie par un = exp(3-0,5n) et la suite (Sn) définie par Sn = u0 +u1 +u2....+un somme des n premiers termes de la suite (un). Question 8 La suite (un): A. est arithmétique de  raison -0,5 B.   est arithmétique de  raison 3 C. est géométrique de  raison e3. D. n'est ni arithmétique, ni géométrique. E. aucune des proposiions proposées n'est correcte. Vrai. un = e3 x e-0,5n ; u0 = e3 ; u1 = e3 x e-0,5 ; u1 = e3 x e-1 = e3 x e-0,5 x e-0,5 =u0  x e-0,5  ; un = e3 x e-0,5 x e-0,5(n-1)=un-1  x e-0,5 . La suite (un) est géométrique de raison e-0,5. Question 9. La suite (Sn) : A. tend vers plus l'infini quand n tend vers plus l'infini. B. tend vers moins l'infini quand n tend vers plus l'infini. C. tend vers zéro l'infini quand n tend vers plus l'infini. D. tend vers u0 e3 /(e3-1) quand n tend vers plus l'infini. E. tend vers u0 e½ /(e½-1) quand n tend vers plus l'infini.Vrai. Sn = u0 (1-e-0,5(n+1) / (1-e-0,5) tend vers u0 / (1-e-0,5) = u0 e½ /(e½-1) quand n tennd vers plus l'infini. On se place dans le plan complexe orienté. Question  10.   L'ensemble des points M d'affixe z vérifiant |z-i+1| =|z-1| est : A. une droite. Vrai. B.un cercle c. une parabole D. une hyperbole E. un carré. z = x+iy ; z-i+1 = x+1+i(y-1) ; |z-i+1| =( (x+1)2+(y-1)2 )½. z-1 = x-1 +iy ; |z-1| =( (x-1)2+y2 )½. (x+1)2+(y-1)2 = (x-1)2+y2  ; 4x-2y+1=0 ; y =2x+0,5. .. .. Question 11 Les points M d'affixe z solutions de l'équation z4 = 16 sont : A. tous alignés B. sur un cercle de centre O et de rayon 16. C. les sommets d'un carré dont la longueur de la diagonale vaut 2. D. les sommets d'un carré dont la longueur de la diagonale vaut 4. Vrai. E. les sommets d'un carré dont la longueur de la diagonale vaut 32. On pose Z = z2 ; Z1 = 4 et Z2 = -4. z1 = 2 ; z2 = -2 ; z3 = 2i ; z4 = -2i. Dans le plan complexe orienté on considère l'équation (E) : z4 +z3 +5z2+z+4=0. Question 12 L'équation (E) admet exactement : A. aucune racine imaginaire pure B. une racine imaginaire pure.  C. deux racines imaginaires pures. Vrai. D. trois racines imaginaires pures. E. quatre racines imaginaires pures. Si  z = i ; z2 = -1 ; z3= -i ; z4= 1 ; 1-i-5+i+4 = 0 est vérifié. Si  z = -i ; z2 = -1 ; z3=+i ; z4= 1 ; 1+i-5-i+4 = 0 est vérifié. (E) s'écrit : (z+i)(z-i)(z2+z+4)=0 ; (z2+1)(z2+z+4)=0 ; Solutions de : z2+z+4 = 0. Le discriminant étant négatif, il n'y a pas de solutions réelles, mais deux solutions du type z = a+ib avec a et b non nuls. Question 13 L'équation (E) admet exactement : A. aucune racine réelle. Vrai. B. une racine réelle.  C. deux racines réelles. D. trois racines réelles. E. quatre racines réelles. Question 14 Le nombre de solutions distinctes de (E) de la forme a+ib avec a et b réels non nuls est exactement : A. zéro B. une. C. deux. Vrai D. trois. E. quatre. Question 15. La valeur de l'intégrale suivante est :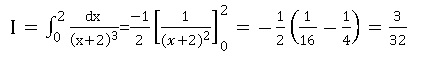 A. 3 ln2. B. 3 / 32. Vrai. C. -3 / 32 D. 3/16. E. aucune des proposiions proposées n'est correcte. Question 16 La valeur de l'intégrale suivante est :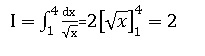 A.  -0,5 B. ln2 C. 1/3 D. 3 E. aucune des proposiions proposées n'est correcte. Vrai. Question 17 La valeur de l'intégrale suivante est :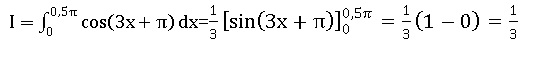 A. 1 /3. Vrai. B. 1 / 4 C. 2 / 3 D. 3 E. 1 Question 18 La valeur de l'intégrale suivante est :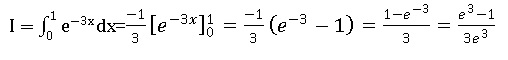 A. e-1. B. (e-3-1) / 3. C. 3(e-3-1). D. -3(e-3-1).. E. (e-3-1) / (3e3). Vrai. Question 19 Une primitive de la fonction x(x2+3) est ; A. x2(x3+3x). Faux ( la primitive de cette fonction est en x4). B. 0,5x2(x3/3 +3x). Faux.. C. 0,25(x2+3)2. Vrai. On dérive en posant u = x2+3 ; u' = 2x ; 2uu' = 4x(x2+3) puis multiplier par 0,25 : x(x2+3). D. 0,5(x2+3)2. Faux. E. aucune des solutions proposées n'est correcte. Faux. Question 20 La fonction sin2(x) est une primitive de : A. sin(2x). Vrai. B. -sin(2x).  C. sin(x) / 2. D. 2 sin(x). E. aucune des solutions proposées n'est correcte. On dérive sin2(x) en posant u = sin(x) ; u' = cos(x) : 2uu' = 2 sin(x) cos(x)= sin (2x) . Question 21. 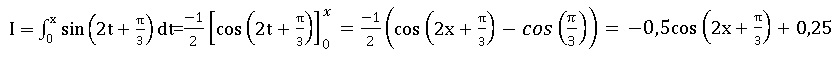L'intégrale suivante est égale à : A. 0,5 cos(2x+p/3)-0,5. B. -0,5 cos(2x+p/3) +0,25. Vrai. C. 0,5 sin(2x+p/3)-0,25. D. 2cos(2x+p/3)-1. E. -0,5 (cos2x+p/3)+p/6.

menu