Perception
auditive, effet de masque, haut-parleur,
concours audioprothésiste Nancy 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
I. Perception
auditive. Effet de masque.
Les oreilles captent les sons et le cerveau les interprète.
Données : débit binaire lors de la lecture d'une musique enregistrée
sur CD : 1,41 106 bits / s.
1 octet = 8 bits. I0 = 1,0 10-12 W m-2.
Le cerveau a la capacité de reconstituer des informations manquantes
pour construire une perception auditive interprétable. C'est le cas
pour un son musical dont on perçoit la hauteur bien que sa fréquence
fondamentale ait été supprimée. Un son joué par un piano est numérisé
puis transmis. On donne son spectre ( figure 1). La fréquence
fondamentale a été supprimée au cours d'un traitement spécifique du
signal.
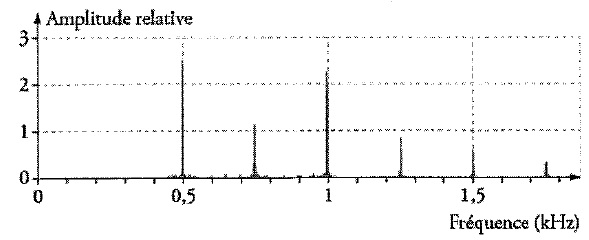
1. Déterminer la
hauteur du son.
Les fréquences des harmoniques ( 0,5 ; 0,75 ; 1 ; 1,25 ; 1,5 kHz) sont
des multiples du fondamental.
La hauteur du son est 0,25 kHz.
2.
Si 2 sons purs sont écoutés simultanément, le plus intense, appelé "
son masquant", peut créer une gène sur la perception du second, le son
masqué. Il peut même le rendre inaudible. La comparaison des courbes
suivantes permet de mettre en évidence ce phénomène appelé " effet de
masquage"..
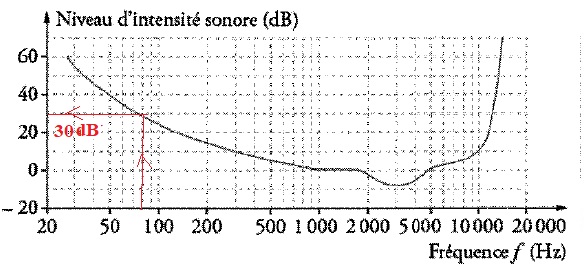
Valeurs minimales de niveau d'intensité sonnore audible ( seuil
d'audition) pour un normo-entendant en fonction de la fréquence lorsque
le son est écouté dans un environnement silencieux.
a Déterminer
le niveau d'intensité sonore
minimal pour qu'un son de fréquence 80 Hz soit audible pour un
normo-entendant. 30 dB.
b. Montrer que la
fréquence de référence à laquelle correspond l'intensité I0
est 1000 Hz.
Le niveau d'intensité sonore vaut 0 à une fréquence de 1000 Hz.
0 = 10 log (I / I0) ; par suite I = I0.
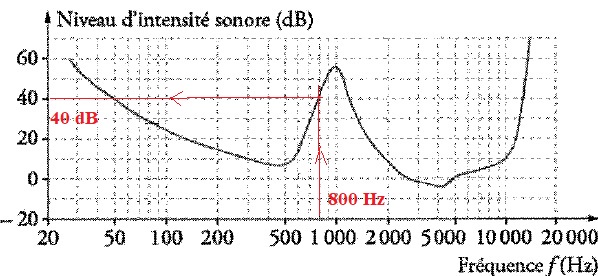
Valeurs
minimales de niveau d'intensité sonnore audible ( seuil d'audition)
pour un normo-entendant en fonction de la fréquence lorsque le son est
écouté simultanément avec un son pur de fréquence 1 kHz et de niveau
d'intensité sonore 55 dB..
c. Déterminer le
niveau d'intensité minimal pour qu'un son de fréquence 800 Hz soit
audible en présence d'un son masquant de fréquence 1 kHz et de niveau
sonore 55 dB.
d. Le format MP3
exploite l'effet de masquage pour compresser l'enregistrement numérique
d'un signal sonore. Cela consiste à réduire l'information à stocker
sans trop dégrader la qualité sonore du signal. La compression permet
de réduire la taille d'un fichier d'un enregistrement musical. Le
spectre fréquentiel de la note La3 jouée par une flûte
traversière dans un environnement silencieux est donnée ci-dessous.
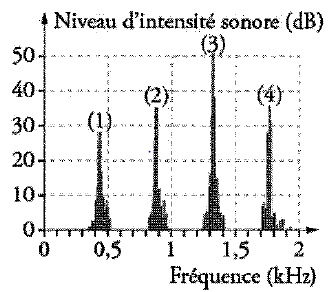 La flûte joue la note La3
en présence d'un son masquant de fréquence 1 kHz et de niveau
d'intensité sonore de 55 dB . L'enregistrement numérique du signal est
compressé au format MP3.
La flûte joue la note La3
en présence d'un son masquant de fréquence 1 kHz et de niveau
d'intensité sonore de 55 dB . L'enregistrement numérique du signal est
compressé au format MP3.
1. Calculer la
période du signal temporel émis par la flûte quand elle joue le La3.
Fréquence du fondamental f = 0,45 kHz = 450 Hz ; période T = 1 / 450 =
2,22 10-3 s.
2. En étudiant
chaque pic du spectre, indiquer celui ou ceux qui seront éliminés par
ce codage MP3. Justifier.
|
Niveau
d'intensité sonore (dB)
|
Niveau
d'intensité sonore
minimale pour être audible
en présence du son masquant
|
Conclusion
|
Fondamental
0,45 kHz
|
29
|
8
dB
|
présent
|
Premier
harmonique 0,9 kHz
|
34
|
50
dB
|
éliminé
|
Second
harmonique 1,35 kHz
|
50
|
30
dB
|
présent
|
troisième
harmonique 1,8 kHz
|
37
|
15
dB
|
présent
|
e.
Une chanson de 3 minutes est enregistrée sur un CD. Cet enregistrement
est compressé au format MP3. Le poids numérique du fichier est égal à
2,88 106 octets. Déterminer le facteur de compression du
format MP3 après en avoir donné une définition.
Débit binaire en lecture : 1,41 106 / 8 = 1,76 105
octets / s.
Soit 1,76 105
x3 x 60 = 3,17 107 octets.
Taux de compression = taille du fichier non compressé / taille du
fichier compressé = 3,17 107 / (2,88 106) = 11.
f. Effet de
masquage lors du passage d'un train.
Dans une ambiance sonore calme, deux personnes conversent à un mètre
l'une de l'autre. L'auditeur perçoit la parole de l'orateur avec un
niveau sonore égal à 50 dB. Un train passe. La parole de l'orateur est
masquée par le bruit du train. On supppose que dans ces conditions, le
bruit du train masque toutes les fréquences audibles. On admet que le
niveau d'intensité sonore minimal audible de la parole est 60 dB en
présence du train quelle sue soit la fréquence.
Pour
être entendu, l'orateur parle plus fort ou se rapproche de l'auditeur.
1.
L'orateur ne se rapproche pas mais parle plus fort. Là où se trouve
l'auditeur, le niveau d'intensité sonore est de 70 dB, déterminer s'il
perçoit un son.
Oui il perçoit la parole car 70 dB est supérieur au niveau d'intensité
sonore minimal audible.
2.
Pour une source émettant de la même façon dans toutes les directions,
l'intensité sonore en un point situé à une distance d de la source est
inversement proportionnelle à d2. Si l'orateur ne parle pas
plus fort, mais se rapproche de l'auditeur, à quelle diqtance de
l'auditeur devra-til se placer pour être audible ?
Intensité minimale audible en présence du trai : I = I0 x 1060/10
= 1,0 10-12 x 106 = 1,0 10-6 W m-2.
Intensité sonore de l'orateur à une distance de 1 m : I0 x 1050/10 = 1,0
10-12 x 105 = 1,0 10-7 W m-2.
1,0 10-6
/ 12 = 1,0 10-7
/ d2 ; d2 =0,1 ; d = 0,316 m.
Il doit se rapprocher de 1 -0,316 =0,684 m.
|
|
II. Etude
d'un haut-parleur.
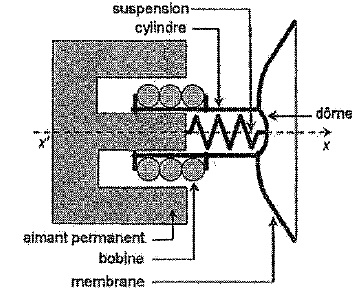
La
partie mécanique d'un haut-parleur électrodynamique est constituée
d'une membrane mobile, solidaire d'un cylindre creux sur lequel est
enroulé le fil d'une bobine en cuivre. L'ensemble, appelé équipage
mobile, possède une masse m et est astreint à se déplacer selon l'axe
xx'. La suspension est modélisée par un ressort de constante de raideur
k, de longueur à vide l0 pouvant travailler en extension
comme en compression.
1. Etude théorique du mouvement de
l'équipage mobile en absence de frottement.
L'équipage mobile est modélisé par un solide S, de masse m, de centre
d'inertie G, assujetti à se déplacer sans frottement sur une tige
horizontale. Ce solide est attaché à un ressort à spires non jointives,
de masse négligeable et de constante de raideur k. La position du
solide est repérée par l'abscisse x de G. La position du point G à
l'équilibre correspond à l'origine O des abscisses. Le référentiel
d'étude est le référentiel terrestre supposé galiléen.
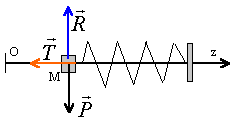
a. Faire
l'inventaire des forces qui s'exercent sur le solide S à la date t. Les
représenter sur un schéma simplifié, sans souci d'échelle.
Trois forces s'exercent sur S : le poids, la réaction de la tige et la
force de rappel exercée par le ressort.
b. Ecrire l'expression de la force
de rappel T du ressort en fonction de l'abscisse z.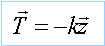
c.
En appliquant la seconde loi de Newton au solide, vérifier que
l'équation différentielle du mouvement de G à la date t peut se mettre
sous la forme :
z" +k / m z = 0.
La relation fondamentale de
la dynamique s'écrit :
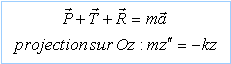
d. Une solution de l'équation
différenteille précédente est de la forme z(t) = Zm cos ( 2pt / T0 ) où Zm
est une constante.
Montrer que T0 = 2p(m/k)½.
L'équation différentielle est celle d'un oscillateur harmonique de
pulsation w = (k
/ m)½= 2 p
/ T0.
Par suite T0 = 2p(m/k)½.
e. Par analyse
dimensionnelle, vérifier l'homogénéité de cette expression.
T s'exprime en
seconde ; m s'exprime en kg ; k s'exprime en N m-1 soit kg m
s-2 m-1 ou kg s-2.
m / k s'exprime en s2 ; (m / k)½ s'exprime en
seconde ; 2p est
sans dimension.
2. Etude expérimentale du mouvement
de l'équipage mobile.
On
se propose de déterminer la masse m de l'équipage mobile et la
constante de raiseur k du ressort. La membrane étant initialement au
repos, on frappe légèrement avec le doigt son dôme d'un coup unique et
rapide, puis on déclenche l'acquisition. On obtient les variations au
cours du temps de l'abscisse de son centre d'inertie.
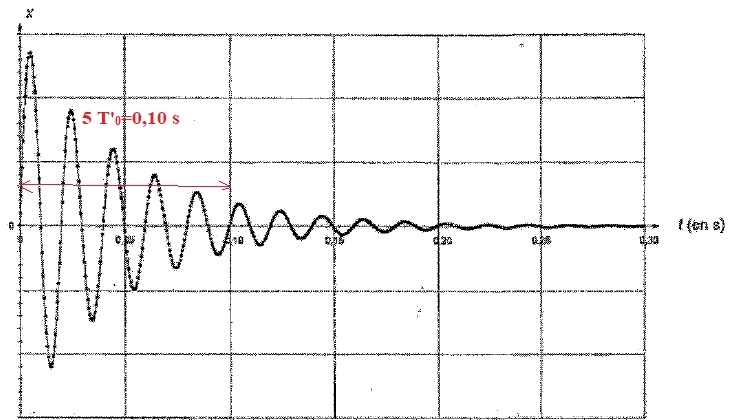
a. Quelle est la nature des
oscillations et quel est le nom du régime qui leur est associé ?
Les oscillations sont pseudo-périodiques. Le régime est sinusoïdal
amorti.
b. Interpréter
l'évolution temporelle de l'amplitude des oscillations.
Du fait des frottements, l'amplitude des oscillations diminue au cours
du temps.
c. Déterminer la
valeur de la pseudo-période T'0 des oscillations et en
déduire, dans l'hypothèse d'un amortissement faible, la valeur de la
fréquence propre f0 de l'équipage mobile.
T'0 = 0,02 s ; f0 = 1 / 0,02 = 50 Hz.
d. On fixe au dôme
une masse additionnelle m' = 10 g. La fréquence propre de l'ensemble
devient f '0 = 45 Hz.
Exprimer f '0 en fonction de k, m et m'.
f ' 0 = 1 / (2p)[k
/ (m +m')]½. f
0 = 1 / (2p)[k
/ m ]½.
f 0 / f '0 = [(m +m')/ m ]½ ;
(f 0
/ f '0 )2=1+ m' / m.
m = m ' / [ (f 0 /
f '0 )2-1]
= 10 /[( 50/45)2-1] =42,6 g.
Par la suite on prendra m = 40 g.
e. Exprimer k en
fonction de f0. En déduire k.
k = f02 4 p2
m = 502 x4 x3,142 x0,040 ~3,94 103 N m-1.
f. Après avoir déconnecté l'interface, on branche aux bornes du
haut-parleur un GBF qui impose un signal sinusoïdal de fréquence f est
d'amplitude non nulle constante.
A quel type d'oscillations est soumis l'équipage mobile ?
Oscillations forcées.
En admettant un amortissement faible, qu'observe-ton lorsque f est au
voisinage de f0 ? Quel est le nom de ce phénomène ?
L'amplitude passe par un maximum. Phénomène de résonance.
g. On test
maintenant un deuxième haut-parleur endommagé. On obtient les
variations au cours du temps de l'abscisse x de son centre d'inertie G
de l'équipage mobile.
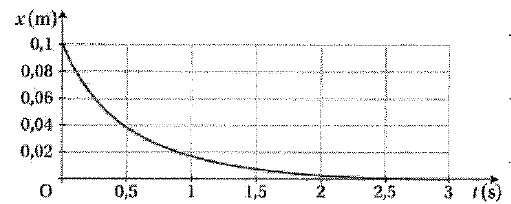
Quel est le type de régime observé ?
Régime apériodique.
Quelle est la cause de la défaillance de l'équipage mobile ?
Les frottements sont devenus trop importants.
|
|
III. Etude de la mécanique.
Au
rugby, une chandelle désigne un coup de pied permettant d'envoyer le
ballon en hauteur par dessus la ligne de défense adverse. L'objectif
pour l'auteur de cette action est d'être au point de chute pour
récupérer le ballon derrière le rideau défensif.
On se place dans le référentiel terrestre supposé galiléen. On néglige
les actions de l'air.
Le joueur A est animé d'un mouvement rectiligne uniformr de vitesse v1.
Il réalise une chandelle.
On définit un repère sont l'origine est la position initiale du ballon
Le
graphique ci-dessous représente la
trajectoire du ballon dans le repère choisi.
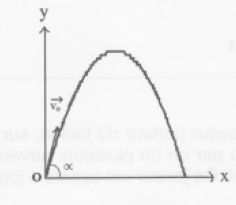
A t= 0 l
e
vecteur vitesse fait un angle a
= 60° avec l'axe Ox et sa valeur est v0 = 10,0 m/s.
1. Etablir les coordonnées ax
et ay du vecteur accélération du point M représentant le
ballon.
Le ballon est en chute libre, il n'est soumis qu'à son poids. Ecrire la
seconde loi de Newton :
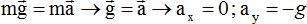
2. Montrer que les
équations horaires du mouvement du point M sont : x =v0cos a t ; y = -½gt2 +
v0 sin a
t.
La
vitesse est une primituve du vecteur accélération :
vx = constante = v0cos
a ;
vy = -gt + constante ; vy(t=0) = v0
sin a ; vy
= -gt +v0
sin a .
Le vecteur position est une primitive du vecteur vitesse. La position
initiale étant confondues avec l'origine du repère, les constantes
d'intégration seront nulles.
x =v0cos
a t ;
y = -½gt2 + v0 sin a t.
3. En
déduire l'équation de la trajectoire du point M.
t = x /
(v0cos
a) ;
repport dans y :
y = - ½gx2
/ (v0cos
a)2
+ x tan a.
4. Déterminer
par le calcul le temps dont dispose le joueur pour récupérer le ballon
avant que celui-ci ne touche le sol.
-4,9 t2
+8,7 t = 0 ; t = 0 ( position
initiale ) et t = 8,7 / 4,9 =1,8 s.
5. Déterminer de deux manières
différentes la vitesse v1 pour que la chandelle soit réussie.
Distance parcourue par le joueur entre l'instant de la frappe et
l'instant de la récupération :
x =v0cos a
t.
Vitesse du joueur animé d'un mouvement rectiligne uniforme : v1
=x/t = v0cos
a
= 10,0 cos 60 = 5,0 m/s.
Le mouvement du ballon suivant l'axe Ox et le déplacement du joueur
sont identiques : ce sont des mouvements rectilignes uniformes à la
vitesse vx = 5,0 m/s.
IV.
Ondes acoustiques.
Deux microphones M1 et M2, distants de L = 2,00
m, sont reliés respectivement aux voies 1 et 2 d'un oscilloscope. Un
émetteur E est placé entre les deux microphones. A l'instant t = 0, il
commence à émettre une onde sonore qui se propage vers les deux
microphones. On obtient les oscillogrammes suivants. La durée de
balayage est 2 ms / div.
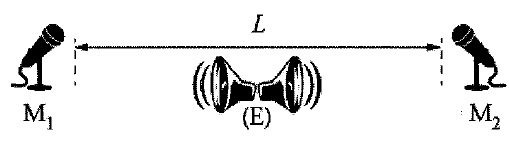
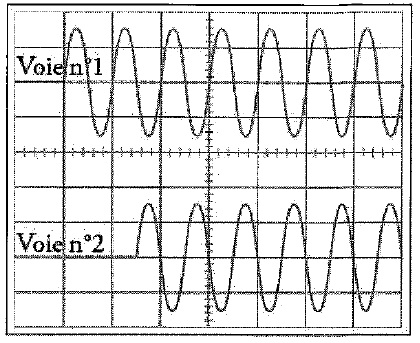
Célérité du son dans l'air c = 340 m / s.
Pour chaque affirmation, indiquer si elle est vraie ou fausse.
Justifier.
1. L'onde sonore
est une onde mécanique longitudinale. Vrai.
L'onde sonore nécessite un milieu de propagation. La variation de
pression se propage dans la direction de l'onde.
2. la longueur
d'onde vaut 0,34 m. Faux.
La période est égale à une division soit 2 ms ou 2,10-3 s.
l = c
T = 340 x 2 10-3 = 0,68 m.
3. L'émetteur est à
0,49 m du microphone M1. Vrai.
Retard
de l'onde arrivant en M2 par rapport à M1 : 1,5
div soit 3,0 ms.
3,0 10-3 x 340 =1,02 m.
(2-1,02) / 2 = 0,49 m.
4. L'onde atteint plus rapidement
les microphones si on double la fréquence. Faux.
L'air n'est pas un milieu dispersif pour les ondes sonores.
V. Une chute libre.
Une balle de masse m est lancée d'une hauteur h = 1,5 m avec une
vitesse initiale v0. On note vx la composante de
la vitesse sur l'axe horizontal et vy sa composante sur
l'axe vertical orienté vers le haut. L'évolution des deux composantes
du vecteur vitesse avec le temps est représentée.
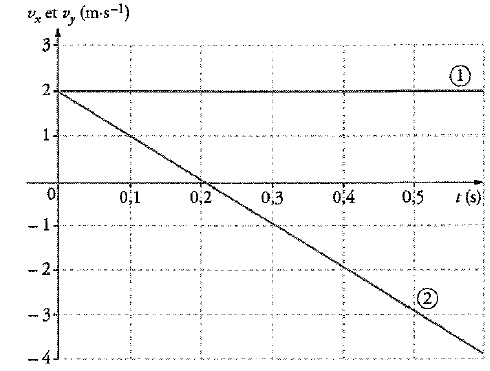
Pour
chaque affirmation, indiquer si elle est vraie ou fausse. Justifier.
1. la valeur de la vitesse initiale
vaut v0 = 4,0 m /s. Faux.
v0 = (v0x2 +v0y2)½
= (22 +22)½ = 2,83 m /s.
2. L'angle a est égal à 45°. Vrai.
v0x = v0 cos a = voy = v0
sin a = 2
3. Au sommet de la
trajectoire, la balle a une vitesse nulle. Faux.
Au sommet seule la composante verticale de la vitesse est nulle.
4. A l'instant t =
0,20 s, la balle est à nouveau à la hauteur h. Faux.
A t = 0,20 s, la composante verticale de la vitesse s'annule puis
change de signe. La balle se trouve au sommet de la trajectoire.
|
|