Equilibres
chimiques, Médecine Paces.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
QCM
1.
Quelle(s) combinaison(s) de coefficients stoechiométriques permet(ent)
d'équilibrer ka réaction d'oxydation de l'ammoniiac en monoxyde d'azote
et eau.
a NH3(g) + b O2(g) = c NO(g) + d H2O(g).
Le nombre d''oxydation de l'azote passe de -3 à +2 et celui de l'oxygène de 0 à -2.
2 NH3(g) + 2,5 O2(g) = 2 NO(g) + 3 H2O(g).
4 NH3(g) + 5 O2(g) = 4 NO(g) + 6 H2O(g).
A. a = 4 : b = 5 ; c = 4 ; d = 6. Vrai.
B. a = 1 ; b = 2,5 ; c = 1 ; d = 1,5
C. a = 1 ; b = 1,5 ; c = 1 ; d = 3.
D. a = 2 ; b = 2,5 ; c = 2 ; d = 3. Vrai.
E. a = 1 ; b = 1,25 ; c = 1 ; d =1 ,5. Vrai.
QCM2.
Quelle(s) réaction(s) parmi les suivantes correspond'ent) à la réaction
de formation de la pyridine liquide dans les conditions standards ?
A. 5 C graphite + 5 H2(g) +½N2(g) --> C5H5N (l).
B. 10 C graphite +2, 5 H2(g) +N2(g) --> 2C5H5N (l).
C. 10 C graphite +5 H2(g) +½N2(g) --> C5H5N (l).
D. 5 C graphite + 2,5 H2(g) +½N2(g) --> C5H5N (l). Vrai.
E. 5 C graphite + 2,5 H2(g) +N2(g) --> 2C5H5N (l).
QCM3.
Quelle est l'énergie thermique libérée lors de la formation de 100 g
d'eau liquide à 298 K sous pression atmosphérique selon la réaction
explosive :
2H2(g) + O2(g) ---> 2H2O(l). DrH° = -570 kJ.( pour deux moles d'eau formées)
Quantité de matière d'eau : 100 / 18 = 5,56 mol ; 5,56 x (-570) /2 = -1583 kJ.
A. -1583 kJ mol-1.
B. -570 kJ.
C. +1583 kJ
D. -1583 kJ. Vrai.
E. -2,5 kJ mol-1.
Exercice 1.
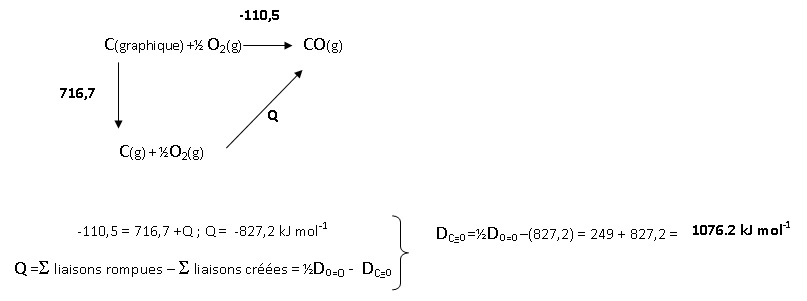
Déterminer l'énnergie de la liaison C=O
dans le monoxyde de carbone à partir des données suivantes à 25 °C :
enthalpie molaire standard de formation du monoxyde de carbone CO (g) DfH° = -110,5 kJ mol-1 ; DsubH° (C graphite)= 716,7 kJ mol-1 et énergie de liaison DO=O = 498 kJ mol-1.
A. +571,5 kJ.
B. +1076,2 kJ mol-1. Vrai.
C. -108,2 kJ mol-1.
D. -1076,2 kJ mol-1.
E. +1076,2 kJ.
Exercice 2 .
On consodère la réaction suivante :
2 NO2(g) = 2NO(g) + O2(g).
A une pression totale de 1 bar : DrG° ( kJ mol-1) = 114,2 -0,146 T.
1. Quelle relation littérale lie l'enthalpie libre standard de réaction DrG° , l'enthalpie standard de réaction DrH° et l'entropie standard de réaction DrS° ?
DrG° = DrH° -T DrS°.
2. Quelle information sur ces dernières grandeurs peiut-on déduire du fait que DrG° est une fonction linéaire de la température ?
DrH° et DrS° sont indépendantes de la température.
3. Donner les valeurs numériques de DrH° et DrS°.
DrH° = 114,2 kJ mol-1 ; DrS° =0,146 kJ mol-1 K-1.
4. Commenter le signe de DrH° et DrS°.
DrS° est positive, le désordre augmente ( il y a 3 molécules parmi les produirts et 2 parmi les réactifs).
5. Quelle est l'influence sur le sens d'évolution de cet équilibre :
- D'une augmentation de température à pression constante.
La réaction est endothermique ( DrH°
>0) ; la réaction est favorisée ( équilibre déplacé dans le
sens direct ) par une augmentation de température à pression constante.
- D"une augmentation à température constante ?
Il y a 3 moles de produits contre 2 moles de réactifs. Une
augmentation de pression à température constante déplace l'équilibre
dans le sens indirect, diminution du nombre total de molécules.
- L'ajout d'un gaz inerte à volume et température constants ?
L'ajout dun gaz inerte à volume et température constants correspond à une augmentation de pression : l'équilibre est déplacé dans le sens indirect.
6. Calculer la valeur de la constante d'équilibre à 300 K et à 1000 K.
DrG° ( kJ mol-1) = - RT ln K = 114,2 -0,146 x300 = 70,4 kJ mol-1 = 7,04 104 J mol-1.
ln K = - 7,04 104 / (8,314 x300) = -28, 225 ; K = 5,5 10-13.
DrG° ( kJ mol-1) = - RT ln K = 114,2 -0,146 x1000 = -31,8 kJ mol-1 = -3,18 104 J mol-1.
ln K = 3,18 104 / (8,314 x1000) = 3,82 ; K = 45,6.
7.
La pression partielle du dioxygène étant constante et égale à 0,2 bar,
calculer le rapport entre les nombres de moles des deux oxydes d'azote
à l'équilibre à ces deux températures. Conclure.
K = P(O2) x [PNO / PNO2 ]2. [PNO / PNO2 ] = (K / 0,2)½.
A 300 K : [PNO / PNO2 ] = (5,5 10-13 / 0,2)½=1,65 10-6.
A 1000 K : [PNO / PNO2 ] = (45,6 / 0,2)½=15,1.
La
réaction est favorisée ( équilibre déplacé dans le sens direct )
par une augmentation de température à pression constante.
|
|
|
|
|
Exercice 3 :
Le glucose joue un rôle de carburant pour certaines cellules, en
fournissant l'énergie nécessaire à leur survie, et à leur
fonctionnement. La combustion complète à 298 K du glucose C6H12O6(aq) en présence de dioxygène a pour seuls produits H2O(l) et CO2(g).
1. Ecrire l'équation de la réaction.
C6H12O6(aq) + 6 O2(g) -->6 H2O(l) + 6 CO2(g)
2.
Quelle est la chaleur dégagée = 298 K par la combustion de 5,0 g de
glucose dans les conditions standards ? La réaction est-elle
exothermique ou endothermique ?
Dr H° = 6 Df H° (CO2(g)) + 6 Df H°(H2O(l)) - 6Df H°(O2(g)) - Df H°(C6H12O6(aq).
Dr H° = 6 x(-393,5) +6 x(-285,6) -6 x0 -(-1293) = -2781,6 kJ mol .
Dr H° est ngatif, la réaction st exothermique.
Masse molaire du gluxose m = 6 x12 + 12 +6 x16 = 180 g / mol.
Quantité de matière contenue dans 5,0 g de glucose : 5,0 / 180 =0,0278 mol.
Energie libérée : 0,0278 x (-2781,6) = - 77,3 kJ.
3. En admettant que
les enthalpies et entropies de réaction sont indépendantes de la
température, calculer l'enthalpie libre standard de cette réaction à
310 K ( température du métabolisme humain ).
Dr S° = 6 S° (CO2(g)) + 6 S°(H2O(l)) - 6S°(O2(g)) - S°(C6H12O6(aq).
Dr S° = 6 x213,7 +6 x70,0 -6 x205 -212 = 260,2 J mol .
DrG° = DrH° -T DrS°. = -2781,6 -310 x 0,2602 = -2862,3 kJ / mol.
Soit pour 5,0 g de glucose ( 0,0278 mol) : -2862,3 x 0,0278 = -79,5 kJ.
4. Dans le plasma
sanguin, la concentration du glucose est de l'ordre de 1,0 g / L.
En admettant que lors de la réaction, les activités de l'oxygène et du
gaz carbonique dissous dans le plasma sont respectivement a(O2) = 2,5 10-6 et a(CO2) = 4,2 10-5, dans quel sens évolue la réaction ?
1 g / L correspond à 1 / 180 = 5,55 10-3 mol / L de glucose.
DrG° ( kJ mol-1) = - RT ln K = -2862,3 103; ln K = 2862,3 103 / (8,314 x310) = 1110 ; K = 2,0 10482.
Quotient initial de la réaction : Q = a6 CO2 x a6 H2O / ( aglucose x a6O2) = (4,2 10-5)6 x 1 / (1 x (2,5 10-6)6) = 2,2 107.
Q < K, la réaction évolue dans le sens direct.
Exercice 4.
On considère la réaction suivante : 3Fe2O3(s) = 2Fe3O4 (s) + ½O2(g).
A 298 K l'entropie standard de la réaction est DrS°=+125,4 J mol-1 K-1.
Les enthalpies de formation des deux oxydes ferrique et magnétique sont respectivement DfH° (Fe2O3)= -821,4 J mol-1 et DfH° (Fe3O4)= -1116,0 J mol-1
1. Déterminer lequel de ces deux oxydes est le plus stable thermodynamiquement à 298 K et sous une pression de O2 pur de 1 bar.
DrH°=2DfH° (Fe3O4)+ 0,5 DfH° (O24)-3DfH° (Fe2O4)=2 x(-1116) +0 -3 x(-821,4)=238,2 kJ.
DrG°=DrH°=- T DrS°=238,2 -298 x 0,1254 = 200,6 kJ = 2,06 105 J.
DrG°=-RT ln K ; ln K = -2,06 105 / (8,314 x 298) = -83 ; K = 7,8 10-37, valeur très faible.
L'équilibre est déplacé en sens indirect. Fe2O3(s) est le plus stable thermodynamiquement à 298 K et sous une pression de O2 pur de 1 bar.
2. Sachant que Fe2O3 est le principal constituant de la rouille, cela vous paraît-il logique ? Justifier.
Oui, Fe2O3(s) est plus stable thermodynamiquement à 298 K que Fe3O4 (s).
Exercice 5. Nombres d'oxydation.
Déterminer le nombre d'oxydation de l'élément souligné dans chaque formule..
NO2 : n.o(N) +2x(-2) = 0 ; n.o (N) = IV.
[Cu(NH3)4]2+ : n.o (Cu) + 4 x(-3+3) = 2 ; n.o(Cu) = +II.
PCl4+. n.o(P +4x(-1) + 1 ; n.o(P) = V.
CH3- CH2 OH ; 2n.o(C) +6-2 = 0 ; n.o(C) = -II.
Exercice 6. Demi-équation électronique.
Equilibrer les demi- équations suivantes.
½O2 +2H+ +2e- ---> H2O.
2H2O +2e- ---> H2+ 2HO-.
AsO43- +2e- +4H+---> AsO2- + 2H2O.
Exercice 7. Réactions d'oxydo-réduction.
Equilibrer les réactions suivantes.
Cr2O72- +6 Br- +14 H+---> 2Cr3+ +3Br2 + 7H2O ( milieu acide).
Le degré d'oxydation du chrome passe de 6 à 3 et celui du brome de -1 à 0.
ClO- + AsO2- +2HO- ---> Cl- +AsO43- +H2O. ( milieu basique).
Le nombre d'oxydation du chlore passe de +1 à -1 et celui de l'arsenic passe de +3 à +5.
3Cl2 + 6OH- ---> 5Cl- + ClO3- + 3H2O.
Dismutation du chlore: Son nombre d'oxydation passe de 0 à -1 daans l'ion chlorure et de 0 à 5 dans ClO3- .
|
|
Exercice 8 Transformation de la Xanthine en acide urique.
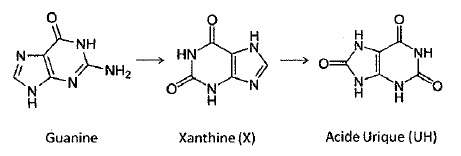
1. L'oxydation de la Xanthine peut être considérée comme résultant des deux couples redox suivant à 298 K.
(1) U- + 3H+ + 2e- = X + H2O. E°1 = -0,36 V.
(2) O2 +4H+ +4e- = 2H2O. E°2 = 0,81 V.
Ecrire l'équation de la réaction d'oxydo-réduction qui serait spontanée
entre ces deux couples dans les conditions standards biologiques à 298
K. Calculer DG°1.
Réduction de l'oxydant le plus fort : O2 +4H+ +4e- = 2H2O.
Oxydation du réducteur le plus fort : 2 X +2H2O = 2 U- + 6H+ + 4e- .
Additionner : O2 +4H+ +4e- +2 X +2 H2O= 2H2O + 2U- + 6H+ + 4e- .
Simplifier : O2 +2 X = 2U- + 2H+ .
K = [U-]2 [H+]2 / ([O2] [X]2).
E2 = 0,81 +0,06 / 4 log([O2] [H+]4 )
E1 = -0,36 +0,06 / 4 log( [U-]2 [H+]6/[X]2 ).
A l'équilibre E1=E2 ; 0,81 +0,06/4 log([O2] [H+]4 ) =-0,36 +0,06 / 4 log( [U-]2 [H+]6/[X]2 ).
0,81 +0,36 = 0,06 / 4 log K ; log K = 1,17 x4 / 0,06 = 78 : K = 1,0 1078.
DG°1= -RT ln K = -8,314 x298 ln(1078) = - 4,4498 105 J mol-1= -444,98 kJ mol-1.
2. L'oxydation de la xanthine en urate à pH = 7 fait intervenir les étapes suivantes.
(II) 2X + 4O2 +2H2O =2U- +4O2- +6 H+. catalysée par la xanthine oxydase.
(III) 4O2- +4 H+ = 2H2O2 +2O2. catalysée par la superoxyde dismutase.
(IV) 2H2O2= O2 + 2H2O. catalysée par la catalase.
2.1. On étudie la réaction de l'étape (II).. Calculer DG°II.
(II) + (III) +(IV) donnent : 2X + O2 =2U- +2 H+. (1).
DG°II + DG°III +DG°IV =DG°1 ; DG°II = DG°1 -DG°III -DG°IV .
DG°III = -121,59 kJ mol-1 ; DG°IV = -196,86 kJ mol-1.
DG°II = -444,98 + 121,59 + 196,86 = -126,53 kJ mol-1.
2.2. Les concentrations stationnaires de O2 et O2- dans le milieu cellulaire sont respectivement 2 10-4 et 10-8 mol L-1. Quel devrait être le rapport des concentrations [U-] / [X] pour que la réaction (II) ne soit pas spontanée dans les conditions cellulaires ?
DG°II doit être nulle ou positive. DG°II = - RT ln KII ; soit KII < 1.
KII = [U-]2[O2-]4 [H+]6 / ([X]2[O2]4) = ([U-] / [X])2 *(10-8)4 *(10-7)6 / (2 10-4)4 =([U-] / [X])2 *6,25 10-60.
([U-] / [X])2 = K / (6,25 10-60) = 1,6 1059 KII.
[U--] / [X] > 4 1029.
|
|