Mathématiques, Bac STL Biotechnologies Métropole 2018

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
Le tableau ci-dessous donne la production d’eau potable d’origine souterraine dans un pays, en millions de m³, entre 2004 et 2014 :

	A	B	C	D	E	F	G
1	Année	2004	2006	2008	2010	2012	2014
2	Rang de l'année x_i	0	2	4	6	8	10
3	Volume d'eau ( millions de m³) y_i	7,5	11,9	14,5	15,9	17	17,9
4	z_i= -2 + ln(y_i)	0,0149	0,4765	0,6741	0,7663	0,8332	0,8848

a. Parmi les formules ci-dessous, indiquer sur la copie, la formule, à entrer dans la cellule B4, qui, recopiée vers la droite, complète la dernière ligne du tableau.
Formule 1 : = −2 + LN($B$3)
Formule 2 : = −2 + LN(B3) ; vrai.
Formule 3 : = −2 + LN(B2)
b. Compléter la ligne 4 du tableau.
2. Dans le repère du plan, représenter le nuage de points M_i ( x_i ; z_i) .
3. Déterminer les coordonnées du point moyen G de ce nuage. Placer le point G sur le graphe.
x_G = (0 +2 +4 +6 +8 +10 ) / 6 = 5.
z_G =(0,0149 +0,4765 +0,6741 +0,7663 +0,8332 +0,8848) / 6 = 0,6083.
4. On souhaite réaliser un ajustement affine de ce nuage de points par la droite D d'équation z = ax +b.
a. À l’aide de la calculatrice, donner les valeurs de a et b arrondies à 10⁻³.
z = 0,0788 x +0,215.
Pour la suite de l’exercice, on prendra z = 0,08x + 0,21 pour équation de la droite D.
b. Construire la droite D.

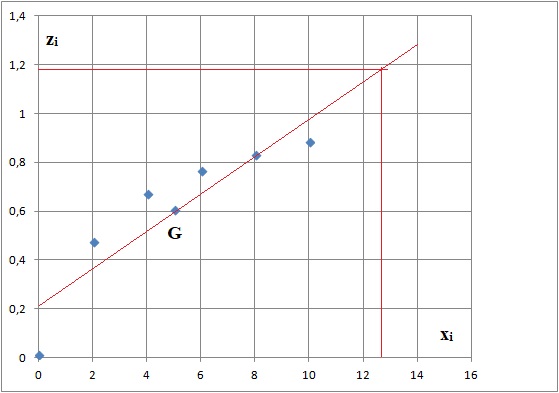
c. Déterminer avec ce modèle d’ajustement, l’année à partir de laquelle le volume d’eau potable d’origine souterraine produit atteindra 24 millions de m³.
z = -2 +ln 24 =1,178 ;
0,08 x +0,21 > 1,178 ; 0,08 x > 0,968.
x > 0,968 / 0,08 = 12,1.
x > 12. Année 2017.

Exercice 2.
Dans cet exercice, tous les résultats seront arrondis à 10^-2.
Une entreprise fabrique des lames de microscope. Une enquête permet d’estimer que la probabilité qu’une lame de microscope, prélevée au hasard dans la production, ne soit pas conforme au cahier des charges est égale à 0,05.
On considère la variable aléatoire X qui, à tout prélèvement de 200 lames de microscope dans la production, associe le nombre de lames de microscope qui ne sont pas conformes au cahier des charges. On suppose que la production est suffisamment importante pour assimiler chaque prélèvement à un tirage avec remise.
On prélève au hasard 200 lames de microscope.
1.a. Justifier que X suit une loi binomiale dont on précisera les paramètres.
Les n expériences sont identiques, indépendantes et aléatoires. deux issues sont possibles ( lame conforme ou lame non conforme ). X suit une loi binomiale B( n= 200 ; p=0,05).
b. Calculer l’espérance mathématique de X, puis l’écart type de X.
Espérance : µ= np = 200 x 0,05 = 10.
Ecart type : s = ( n p(1-p))^½ =(200 x0,05 x0,95)^½ ~3,08.
c. Calculer la probabilité de l’événement suivant : « Exactement 6 lames de microscope parmi les 200 ne sont pas conformes au cahier des charges ».
P(X = 6) = C₂₀₀⁶ x 0,05⁶ x 0,95¹⁹⁴ = 0,061.
d. L’entreprise peut-elle garantir à ses clients qu’au maximum 1 lame de microscope parmi les 200 n’est pas conforme au cahier des charges ? Pourquoi ?
P(X = 0) = C₂₀₀⁰ x 0,05⁰ x 0,95²⁰⁰ = 3,5 10^-5.
P(X = 1) = C₂₀₀¹ x 0,05¹ x 0,95¹⁹⁹ = 3,7 10^-4.
P(X=0) + P(X=1) ~ 4,0 10^-4.
Parmi 10 000 lames de microscopes, il est probable que 4 lames ne sont pas conformes.
Parmi 200 lames de microscopes, il est probable que 0,08 lames ne sont pas conformes.
L'entreprise peut garantir à ses clients qu’au maximum 1 lame de microscope parmi les 200 n’est pas conforme au cahier des charges
2. On décide d’approcher la variable aléatoire X par une variable aléatoire Y qui suit la loi normale d’espérance µ=10 et d’écart type s= 3,08 .
a. Justifier le choix des valeurs prises par µ et s .
10 est l'espérance de la loi binomiale et 3,08 est l'écart type de la loi binomiale.
b. Déterminer la probabilité P(7 < Y < 10). Traduire le résultat obtenu par une phrase.

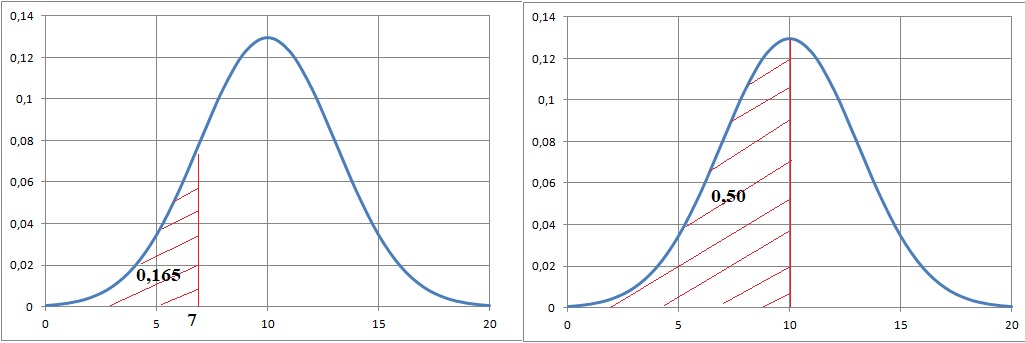
P(7 < Y < 10) = 0,5 - 0,165 = 0,335 ~0,34.
3. Le responsable de la chaîne de production annonce au directeur de l’entreprise que 5 % des lames de microscope produites ne sont pas conformes au cahier des charges.
a. Déterminer l’intervalle de fluctuation asymptotique au seuil de 95 % de la fréquence des lames de microscope qui ne sont pas conformes pour un échantillon de 250 lames de microscope produites.
1,96 (p(1-p)/ n)^½ = 1,96(0,05 x0,95 / 250)^½ =0,027.
Intervalle de fluctuation : [0,05 -0,027 ; 0,05 +0,027] soit [0,023 ; 0,077 ].
b. Un contrôleur qualité de l’entreprise prélève un échantillon de 250 lames de microscope produites dans lequel il trouve 17 lames de microscope qui ne sont pas conformes. Cet échantillon remet-il en cause l’annonce du responsable de la chaîne de production ? Justifier.
17 / 250 = 0,068; cette valeur appartient à l'intervalle [0,023 ; 0,077 ].
Au risque de 5 %, cet échantillon ne remet pas en cause l’annonce du responsable de la chaîne de production.

Exercice 3.
Un sportif fait le test suivant : il court à une vitesse de 6 km h^-1, on déclenche alors un chronomètre à t = 0 minute, puis le sportif augmente sa vitesse de 10 % chaque minute, jusqu’à arrêt de l’effort.
En parallèle, un dispositif permet d’évaluer sa production d’acide lactique après chaque minute d’effort. (L’acide lactique est un déchet qui se forme dans les cellules privées d’oxygène et qui limite les performances physiques.)
Partie A.
Pour tout entier naturel n, on note v_n la vitesse, en km h^-1, de ce sportif, n minutes après le déclenchement du chronomètre. On a : v₀ = 6.
1. Montrer que la suite (v_n) est géométrique. Préciser les valeurs de son premier terme et de sa raison.
Le terme v_n+1 est obtenu en multipliant le terme v_n par 1,1.
Il s'agit d'une suite géométrique de raison 1,1 et de premier terme v₀=6.
2. Déterminer la vitesse de ce sportif 5 minutes après le déclenchement du chronomètre, arrondie à 0,1 km h^-1.
v₁ = 6 x1,1 = 6,6 ; v₂ = 6,6 x1,1 = 7,26 ; v₃ = 7,26 x1,1 = 7,986 ; v₄ = 7,986 x1,1 = 8,785 ; v₅ = 8,785 x1,1 ~9,7.
Ou bien v₅ = 6 x1,1⁵ ~9,7.
3. On considère l’algorithme suivant :
b <---0
v <---6
Tant que v < 12
n <--- n+1
v <---v x1,1
Fin Tant que.
a. Indiquer, dans un tableau, les valeurs successives prises par les variables n et v lors du déroulement de l’algorithme, jusqu’à l’arrêt de celui-ci. Les valeurs prises par v seront arrondies à 10^-1.

n	0	1	2	3	4	5	6	7	8
v	6	6,6	7,3	8,0	8,8	9,7	10,6	11,7	12,9
v < 12	vrai	vrai	vrai	vrai	vrai	vrai	vrai	vrai	faux

b. Quelle est la valeur de la variable n à la fin de l’exécution de l’algorithme ? Interpréter ce résultat par rapport à la situation étudiée.
n = 8. Après 8 minutes de course, la vitesse du sortif atteint 12,9 km h^-1.
Partie B.
On estime que la production d’acide lactique de ce coureur lors de l’effort est modélisée par une fonction f définie sur [0 ;13]. Cette fonction qui au temps t, exprimé en minutes, associe la production d’acide lactique du coureur, exprimée en millimole par litre, à l’instant t, est une solution de l’équation différentielle (E) : y' - 0,17y = 0 sur l’intervalle [0 ;13].
1. Résoudre l’équation différentielle (E) sur [0 ;13].
y = A e^0,17t avec A une constante.
2. On sait que f (0) = 2. En déduire une expression de f (t) pour tout t de [0 ;13].
2 = A e⁰ ; A = 2 ; y = 2 e^0,17t.
3. Pour la suite de l’exercice, on prend pour tout réel t de l’intervalle [0 ;13], y = 2 e^0,17t .
a. Calculer f '(t) . En déduire les variations de la fonction f sur [0 ;13].
f '(t ) =2 x0,17 e^0,17t =0,34e^0,17t.
e^0,17t étant positif, f(t) est strictement croissante sur [0 ;13].
b. Tracer la courbe représentative de la fonction f .

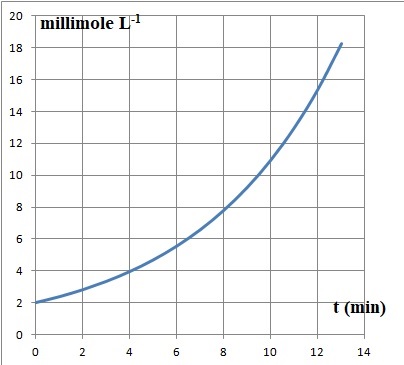
c. On estime que le sportif arrête son effort lorsque le taux d’acide lactique dépasse 15 millimoles par litre. Au bout de combien de minutes ce sportif arrêtera-t-il son effort ? On donnera ce résultat à la minute supérieure et on évaluera alors la vitesse obtenue à 0,1 km h^-1 près.
15 = 2 e^0,17t ; ln(15 / 2) = 0,17 t ; t ~11,85 soit 12 minutes.
v₁₂ = 6 x1,1¹² ~18,8 km h^-1.
4. Un autre sportif, produisant moins d’acide lactique, est soumis au même test. Son taux d’acide lactique est donné par la fonction g définie sur [0, 13] par g(t) =2e^kt où k est un réel positif. En comparant cette situation avec la précédente, que peut-on dire sur le coefficient k ?
g(t) < f(t) ; g(t) / 2 < f(t) / 2 ; e^kt < e^0,17t ;
La fonction exponentielle étant strictement croissante, k < 0,17.

Exercice 4.
Soit f la fonction définie sur [0 ; 3 ] parf(x) = x exp(-x²), f ' sa fonction dérivée. On nomme (C) la courbe représentative de la fonction f dans un repère orthogonal d’origine O. Soit le point B(0,5;0,5). La droite (OB) est tangente à la courbe (C) au point O.
On nomme I l’aire située entre la courbe (C), l’axe des abscisses et les droites d’équation x =0 et x =1. Ci-dessous, on a représenté la courbe (C) et la droite (OB) :

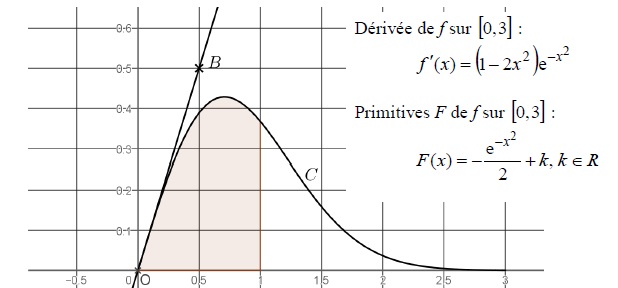
Ci-dessous, on donne quatre affirmations concernant cette fonction f.
Indiquer sur la copie si l’affirmation proposée est vraie ou fausse. Toute réponse sera justifiée.
Affirmation 1 : f '(0) =1. Vrai.
f '(0) = (1-2*0²)e^-0 = 1.
Le coefficient directeur de la droite OB, au point O, est égal à 1.
Affirmation 2 : pour tout x appartenant à [0,3], f '(x) > 0. Faux.
exp(-x²) est positif ; le signe de f '(x) est celui de 1-2x².
1-2x²= 0 soit x = ±0,707.
f '(x) est positive sur [0 ; 0,707[ et négative sur ]0,707 ; 3 ].
Affirmation 3 : l’aire I est supérieure à 0,15 unité d'aire. Vrai.
I = F(1)-F(0) = -1 /(2e) - (-0,5) = 0,5 -1 /(2e) ~0,316 unité d'aire.
Affirmation 4 : la primitive G de la fonction f qui s’annule en 0 est définie pour tout x de [0,3] parG(x) = (-exp(-x²) +1) / 2. Vrai.
G(0) = -e⁰ / 2 +k = 0 ; -0,5 +k = 0 ; k = 0,5.
G(x) = (-exp(-x²) +1) / 2.