Mathématiques,
Bac STL Biotechnologies Polynésie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
La plus ancienne méthode de conservation des aliments pratiquée par
l’homme est la déshydratation.
Ce procédé consiste à
utiliser une source de chaleur pour faire évaporer de l’eau d’un
aliment.
Dans tout l’exercice, on
s’intéresse à un abricot frais placé dans un séchoir pour le
déshydrater.
Avant déshydratation, cet
abricot frais a une masse de 45 g dont 85 % d’eau. Le processus de déshydratation s’achève lorsque cet
abricot a une masse de 9 g dont 25 % d’eau, il bénéficie alors de l’appellation « abricot sec ».
1. Calculer la masse d’eau contenue
dans cet abricot frais.
45 x0,85 = 38,25 g.
2. Vérifier que cet abricot ayant
l’appellation « abricot sec » ne contient plus que 2,25 g d’eau.
9 x0,25 = 2,25 g.
Soit f la fonction
qui, à toute durée t exprimée en heures, associe la masse d’eau (en
grammes) contenue dans cet
abricot placé dans le séchoir depuis t heures. On admet que pour tout
réel t de l’intervalle [0
;13], f(t) = 38,25 e-0,26t
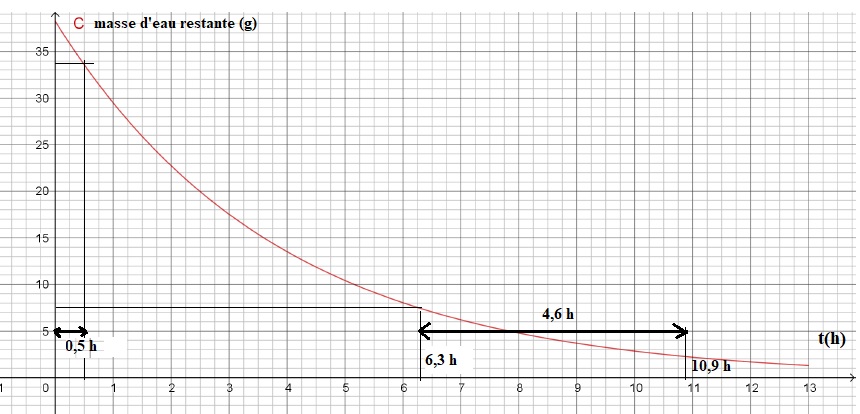
. On a tracé la courbe représentative C de la fonction f.
3. a. Calculer
la masse d’eau présente dans cet abricot après deux heures passées dans
le séchoir. On arrondira à 10-2
g.
f(2) = 38,25 e-0,26 x2 ~22,74 g.
b. Si on laisse cet abricot dans le
séchoir pendant 8 heures, pourra-t-il bénéficier de l’appellation « abricot sec » ? Justifier
votre réponse.
Masse d'eau
présente : f(8) = 38,25 e-0,26 x8 ~4,78 g, valeur supérieure
à 2,25 g.
Non, il ne peut pas bénéficier de la mention abricot sec.
c. Déterminer le temps de séchage
nécessaire pour que l’abricot placé dans le séchoir puisse bénéficier de l’appellation « abricot sec
». On donnera le résultat à la minute près.
f(t) = 2,25.
38,25 e-0,26t = 2,25 ; -0,026 t = ln(2,25 / 38,25) ;
0,26 t = 2,833 ; t ~10,9 h ( 10 h 53 min).
4. On considère maintenant la
totalité du processus de déshydratation qui permet de passer de l’abricot frais, contenant 38,25 g d’eau,
à l’abricot ayant l’appellation « abricot sec », contenant 2,25 g d’eau.
Camille affirme : « dans
ce processus, le temps nécessaire pour éliminer les 5 derniers grammes d’eau est environ 15 fois le temps
nécessaire à l’élimination des 5 premiers grammes d’eau ! ».
Cette affirmation
est-elle exacte ? Justifier. On pourra utiliser la représentation
graphique.
Durée pour éliminer les 5 premiers grammes d'eau.
38,25 -5 = 33,25 = f(t) = 38,25
e-0,26t.
-0,26 t = ln(33,25 / 38.25) ; t ~0,54 h.
Durée pour
éliminer les 5 derniers grammes d'eau.
2,25 +5 = 7,25 =
f(t) = 38,25 e-0,26t ;
-0,26 t = ln(7,25 / 38,25) ; t ~6,4 h.
10,9 -6,4 = 4,5 h.
4,5 / 0,54 = 8,3. L'affirmation
est fausse.
|
|
|
|
|
Exercice
2.
Un
fabricant a mis au point une machine permettant de fabriquer des blocs
de glace (utilisables sur les bateaux de pêche par exemple).
L’épaisseur des blocs de glace fabriqués dépend du temps de
congélation.
1. Compléter la
troisième ligne du tableau ci-dessous. Les valeurs seront arrondies au
dixième.
Temps
de congélation (h) ti
|
1
|
2
|
4
|
8
|
12
|
18
|
26
|
Epaisseur
de la glace (cm) yi
|
4
|
8
|
11
|
16,5
|
20,5
|
24,5
|
28,5
|
xi=ln(ti)
|
0
|
0,7
|
1,4
|
2,1
|
2,5
|
2,9
|
3,3
|
2. Représenter le nuage de points de
coordonnées (xi ,yi).
3. Donner une
équation de la droite d’ajustement (d) de y en x.
y = 7,38 x + 2,54.
Pour la suite, on prend comme modèle d’ajustement, la droite (d)
d’équation y = 7,4x + 2,5.
4. Tracer cette
droite (d) dans le repère.

5. Déterminer,
selon le modèle d’ajustement pris, et à l’heure près, le temps
nécessaire pour fabriquer un bloc de glace de 32 cm d’épaisseur.
32 = 7,4 x +2,5 ;
29,5 = 7,4 x ; x = 29,5 / 7,4 ~ 4 heures.
|
|
Exercice 3.
Une colonie de bactéries est mise en culture avec du glucose.
Pendant la 1ére période de 10 minutes, la masse de glucose
absorbé par la colonie de bactéries est égale à 18,3 femtogrammes (1
gramme est égal à 1015 femtogrammes).
Pendant la 2e période de 10 minutes, la masse de glucose
absorbé par la colonie de bactéries augmente de 26 % par rapport à la
masse de glucose absorbé pendant la 1ére période.
1. Justifier que
la masse de glucose absorbé pendant la 2e période de 10
minutes est égale à 23,058 femtogrammes.
18,3 x1,26 = 23,058
femtogrammes.
Dans la suite, on étudie
l’évolution de la masse de glucose absorbé par la colonie de bactéries
en prenant le modèle suivant :
- pour tout entier naturel n supérieur ou égal à 1, on note un
la masse, en femtogrammes, de glucose absorbé pendant la n-ième période
de 10 minutes ;
- pour tout entier naturel n supérieur ou égal à 1, la masse de glucose
un+1
absorbé par la colonie de bactéries pendant la (n+1)-ième période de 10
minutes augmente de 26 % par rapport à la masse de glucose un absorbé
pendant la n-ième période de 10 minutes précédente.
2. a. Préciser les
valeurs de u1 et u2.
u1 = 18,3 femgtorammes.
u1 =
18,3 x 1,26 = 23,058 femgtorammes.
b. Quelle est la nature de la suite(un).
Justifier votre réponse.
Le terme un+1 est obtenu en multipliant le terme un
par 1,26. c'est une suite géométrique de raison 1,26 et de premier
terme u1.
c. Pour tout entier
naturel n supérieur ou égal à 1, exprimer un en fonction de
n.
un = 18,3 x 1,26n-1.
d. Calculer la
masse de glucose absorbé pendant la 7e période de 10
minutes. On donnera un résultat arrondi à 0,1 femtogramme.
u7 = 18,3 x 1,266=73,2
femtogrammes.
3. On considère l’algorithme
suivant :
n <--- 1
u <---18,3
Tant que u < 100
n <---n+1
u <---1,26 x u
Fin Tant que
Quelle est la valeur de la variable n à la fin de l’exécution de
l’algorithme ? Interpréter ce résultat dans le contexte de l’exercice.
18,3 x 1,26n-1
< 100 ;
(n-1) ln(1,26) <
ln(100 / 18,3) ; n-1 < ln(100 / 18,3) / ln(1,26) ; n-1 < 7,34 ; n < 8.
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
un
|
18,3
|
23.058
|
29,1
|
36,6
|
46,1
|
58,1
|
73,2
|
92.3
|
116,3
|
un
<
100
|
vrai
|
vrai
|
vrai
|
vrai
|
vrai
|
vrai
|
vrai
|
vrai
|
Faux.
|
A la fin de l'algorithme n = 9.
Pendant la 8e période de 10 minutes, la masse de glucose
absorbé par la colonie de bactéries est encore inférieure à 100
femtogrammes.
Pendant la 9e
période de 10 minutes, la masse de glucose
absorbé par la colonie de bactéries est supérieure à 100 femtogrammes.
Dans la suite de l’exercice, on s’intéresse à la masse totale de
glucose absorbé depuis le début de la mise en culture. Dans ce cadre,
on exploite la feuille de calcul suivante obtenue à l’aide d’un tableur.
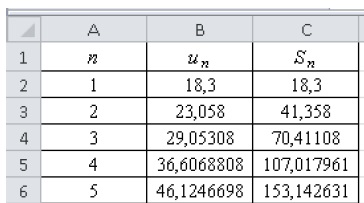
4. a. Interpréter
la valeur de la cellule C4 dans le contexte de l’exercice.
A la fin de la troisième période, la masse totale de glucose consommée
est égale à 70,41 femtogrammes.
b. Quelle formule a
été entrée dans la cellule C3 pour obtenir, par recopie vers le bas,
les valeurs suivantes de la colonne C ?
=SOMME($B$1:B3)
5. Déterminer le
nombre d’heures nécessaire, depuis le début de la mise en culture, à
l’absorption de 1 gramme de glucose par la colonie de bactéries (on
rappelle que 1 gramme est égal à1015 femtogrammes).
Masse totale de glucose : 18,3 10-15 (1-1,26n)
/ (1-1,26) = 1.
1,26n
-1= 0,26 / ( 18,3 10-15) = 1,42 1013.
1,26n ~
1,42 1013.
n ln(1,26) ~ln(1,42 1013) ; n ~131 périodes de 10 minutes
soit environ 22 heures.
Exercice 4.
Dans une ville, un cardiologue s’intéresse à la tension artérielle
(systolique), mesurée en millimètres de mercure (mm Hg), des femmes de
plus de 60 ans.
Partie A.
On note T la variable aléatoire qui, à chaque dossier médical d'une
femme de la ville de plus de 60 ans, associe la tension artérielle de
cette femme mesurée en mm Hg. On suppose que T suit la loi normale
d’espérance µ = 134 et d’écart-type σ = 8,5.
1. Le cardiologue
choisit au hasard le dossier médical d’une femme de plus de 60 ans
parmi les dossiers médicaux des femmes de la ville.
a. Quelle est la
probabilité que la tension artérielle de cette femme soit comprise
entre 130 et 140 mm Hg ? On donnera la valeur arrondie au millième.
b. Quelle est la
probabilité que la tension artérielle de cette femme soit supérieure à
140 mm Hg ? On donnera la valeur arrondie au millième.
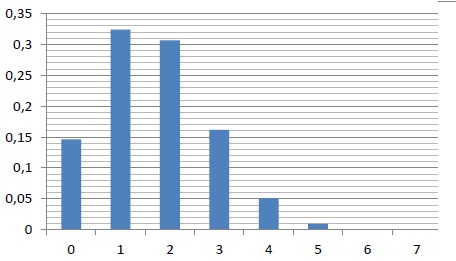
P(130 < X < 140 )= 0,441.
P (X > 140) =
0,240.
2. Donner un nombre
entier h tel que P(134 - h <
T < 134 + h) ~
0,95 (à 10−2 près). Interpréter cette probabilité dans le
contexte de l’exercice.
1-2 P( X < 134+h)
= 0,95.
P( X < 134+h) = 0,025 ;
134+h = 117,3 soit h ~ 16,7 mm Hg.
Partie B.
On admet que 24 % des femmes de plus de 60 ans de la ville étudiée sont
atteintes d’hypertension artérielle. On constitue au hasard un
échantillon composé de 7 dossiers médicaux de femmes de plus de 60 ans
dans la ville étudiée. Le nombre total de dossiers médicaux de femmes
de plus de 60 ans
dans cette ville est suffisamment élevé pour que l’on puisse assimiler
ce prélèvement à un tirage avec remise. On note X la variable aléatoire
qui prend pour valeurs le nombre de dossiers médicaux de femmes
atteintes d’hypertension artérielle dans un échantillon de 7 dossiers
médicaux.
1. Quelle est la
loi suivie par X ? En donner les paramètres.
Les tirages sont indépendants, de même probabilité ; deux issues sont
possibles.
X suit une loi de Bernoulli de paramètre p = 0,24 ; n = 7.
2. On donne
ci-dessous la représentation graphique de la loi suivie par X (en
abscisses, on lit les valeurs prises par k et en ordonnées, les valeurs
prises par P(X = k) ) :
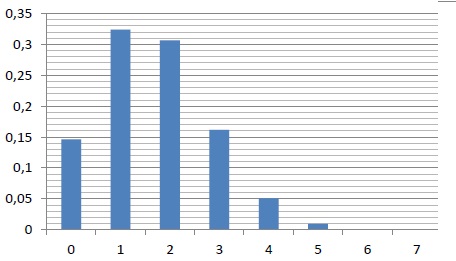
a. À l’aide du
graphique, déterminer une valeur approchée à 0,01 près de la
probabilité pour qu’il y ait au moins 4 dossiers médicaux de femmes
atteintes d’hypertension artérielle dans un échantillon de 7 dossiers
médicaux. On détaillera la démarche.
Au moins 4 signifie X = 4 ; 5 ; 6 ; 7.
P(X =4) + P(X =5) +P(X=6) + P(X=7) = 0,05 + 0,01 +0 +0 = 0,06.
b. Expliquer ce
qui se passe sur la représentation graphique pour X = 6 et X = 7 .
La probabilité
pour qu’il y ait plus de 5 dossiers médicaux de femmes atteintes
d’hypertension artérielle
dans un échantillon de 7 dossiers médicaux est nulle.
Partie C.
Un centre hospitalier universitaire souhaite comparer l’efficacité de
deux régimes alimentaires distincts, notés A et B, destinés à réduire
l’hypertension artérielle dans la population des femmes de plus de 60
ans de la ville.
Il constitue, au hasard, deux groupes de 200 femmes de plus de 60 ans
de la ville souffrant d’hypertension artérielle :
- après avoir suivi le régime A, 15 femmes du premier groupe de 200
femmes n’ont pas de réduction de leur hypertension artérielle ;
- après avoir suivi le régime B, 50 femmes du second groupe de 200
femmes n’ont pas de réduction de leur hypertension artérielle.
En exploitant la notion d’intervalle de confiance, peut-on parler de
différence significative d’efficacité entre les deux régimes
alimentaires en termes de réduction d’hypertension artérielle ?
Régime A :
Proprtion de personnes ayant une réduction de l'hypertension : 185 /
200 = 0,925.
1 / n½ = 200½ ~0,071.
Intervalle de confiance au seuil de 95 % : [0,925-0,071 ; 0,925 +0,071
) soit [ 0,854 ; 0,996 ].
Régime B :
Proprtion de personnes ayant une réduction de l'hypertension : 150 /
200 = 0,75.
1 / n½ = 200½ ~0,071.
Intervalle de confiance au seuil de 95 % : [0,75-0,071 ; 0,75 +0,071 )
soit [ 0,679 ; 0,821 ].
Les deux intervalles de confiance n'ont pas de partie commune. Le
régime A est plus efficce que le régime B.
|
|