Mathématiques,
Bac Sti2d, STL, SPCL, Antilles 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
Le béton est un matériau de construction fabriqué à partir d’un mélange de ciment, de granulats et d’eau.
Selon l’usage prévu (dalle, poutre, fondation …), on utilise des bétons de compositions différentes.
Dans cet exercice, on s’intéresse au béton adapté à la construction
d’une dalle et on étudie la résistance à la compression, exprimée en
MPa (mégapascal), en fonction de la durée t de séchage, exprimée en
jour.
On admet que cette résistance peut être modélisée par une fonction f, définie et dérivable sur l’intervalle [0 ; +oo[ , qui est une solution sur [0 ; +oo[ de l'équation différentielle (E) :
y'+ 0,15y= 4,5.
1. Résoudre l’équation différentielle (E).
Solution générale de l'équation sans second membre : y = A e-0,15t.
Solution particulière de (E): y = 4,5 / 0,15 = 30.
Solution générale de (E) : y = A e-0,15t +30.
2. À l'instant t= 0, la résistance à la compression de ce béton est nulle.
Montrer alors que f est définie sur [0 ; +oo[ par f(t) = -30e-0,15t +30.
f(0) = 0 = A +30 d'où A = -30. par suite f(t) = -30e-0,15t +30.
3. Déterminer la limite de f(t) quand t tend vers plus l'infini et interpréter ce résultat dans le contexte de l’exercice.
e-0,15t tend vers zéro quand t tend vers plus l'infini.
f(t) tend vers 30 quand t tend vers plus l'infini.
Au bout de 30 jours la résistance à la compression est maximale.
4. Il est possible de marcher sur ce type de béton lorsque sa résistance à la compression est supérieure à 12 MPa.
Après combien de jours complets de séchage est-il possible de marcher sur ce type de béton ?
12 = -30 e-0,15t +30 ; 12 / 30 = 0,4= - e-0,15t +1 ;
e-0,15t =0,6 ; -0,15 t = ln(0,6) ; t = 3,4 soit 4 jours.
Exercice 2.
On a représenté ci-dessous une des faces latérales d'une rampe de skate-board que l’on souhaite peindre.
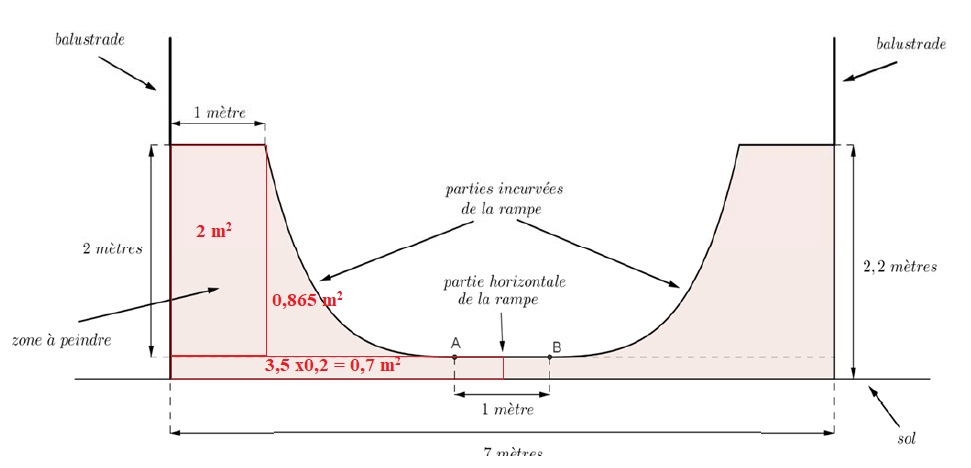
On sait de plus que la face latérale de cette rampe de skate-board admet comme axe de symétrie la médiatrice de [AB] .
Partie A.
On modélise la partie incurvée de la rampe située à gauche de l’axe de
symétrie à l'aide de la fonction f définie et dérivable sur
l’intervalle [0 : 2 ] par :
f(x) = (0,5 x2+ax+b)e-x où a et b sont deux réels que l'on souhaite déterminer.
On a tracé ci-après la courbe représentative C de f dans un repère orthonormal d’unité 1 mètre.
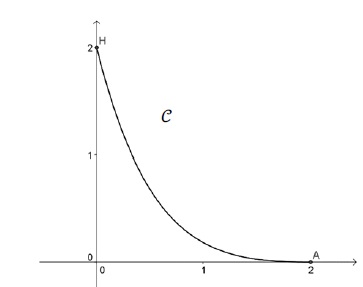
On sait que la courbe C passe par les points A(2 ; 0) et H(0 ; 2) .
1. Déterminer f(0) et f(2).
2. Déduire de la question précédente le système d'équations vérifié par les réels a et b.
3. Déterminer l’expression de f(x).
f(0) =2 = (02+a*0+b)e-0 ; b = 2.
f(2) = 0 = f(x) = (0,5 *22+a*2+b)e-2 = (2+2a+2)e-2 =(4+2a)e-2 ;
4+2a = 0 soit a = -2.
f(x) = (0,5 x2-2x+2)e-x .
|
|
|
|
|
Partie B.
On considère maintenant que la fonction f est définie et dérivable sur l’intervalle [0 ; 2 ] par :
f(x) = (0,5 x2-2x+2)e-x .
1. Calculer f '(x).
On pose u = 0,5 x2-2x+2 et v = e-x ; u' = x-2 ; v' = -e-x.
f '(x) = u'v + v'u = (x-2)e-x - (0,5 x2-2x+2)e-x.
f '(x) = (-0,5 x2+3x-4)e-x.
2. Montrer que la tangente à la courbe C au point A est l’axe des abscisses.
f '(2) = (-0,5 *22+3*2-4)e-2= 0.
Le coefficient directeur de la tangente en A à C est nulle ; de plus A appartient à l'axe des abscisses.
La tangente à la courbe C au point A est donc l’axe des abscisses.
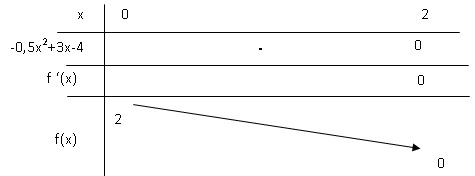
3. Justifier que le signe de f '(x) est donné par le signe du trinôme -0,5 x2+3x-4.
e-x étant positif, le signe de f '(x) est celui du trinôme -0,5 x2+3x-4.
4. En déduire le signe de f'(x) puis le sens de variation de f sur [0 ; 2 ] .
D = 32 -4*4*0,5 = 1.
Solutions de -0,5 x2+3x-4 = 0.
x =(-3 -1) /(-0,5 *2) = 4 et x =(-3 +1) /(-0,5 *2) = 2.
Partie C.
1. Justifier que la fonction f est positive sur l’intervalle [0 ; 2].
La fonction f(x) est strrictement décroissante de la valeur 2 à la valeur 0 sur l’intervalle [0 ; 2].
La fonction f est donc positive sur l’intervalle [0 ; 2].
2. On admet que la fonction F(x) définie par (-0,5 x2+x-1)e-x sur l’intervalle [0 ; 2] est une primitive de la fonction f(x) sur [0 ; 2].
Montrer que l’aire en m2 de la partie délimitée par la courbe C, l'axe des abscisses et les droites d'équation x=0 et x= 2 est égale à 1 -1/e2.
F(2)-F(0) = (-0,5 22+2-1)e-2 -(-0,5 *02+0-1)e-0 = -e-2+1~.
3. En déduire l'aire de la zone à peindre. On donnera une valeur approchée du résultat à 0,01 m2 près.
2 x( 0,7 +2 +0,865)~7,13 m2.
Exercice 3.
Une éolienne est un générateur qui produit du courant électrique à partir de l’énergie cinétique du vent.
Une entreprise européenne réalise la conception, la fabrication, la
vente, l'installation ainsi que l'exploitation et la maintenance de ses
éoliennes.
Son service de presse a publié un article en janvier 2017 dont voici un extrait :
« Une de nos usines située en Espagne, en exploitation depuis 2001, a
produit au total plus de 40 000 pales d'éoliennes de 2001 à 2016, pales
qui ont été exportées vers cinq continents. »
On dispose également des données suivantes sur la production de l’usine espagnole considérée.
Année
|
Quantité de pales produites pendant l'année
|
2001
|
800
|
2008
|
2002
|
Partie A.
Le but de cette partie est de trouver une suite modélisant au mieux la
production des pales d'éoliennes de l'usine espagnole depuis 2001. On
étudie deux modélisations.
1. Dans cette
question, on se propose de modéliser le nombre de pales produites par
l’usine espagnole pendant l'année 2001+n , où n est un entier naturel,
par la valeur arrondie à l’entier le plus proche de un où un = 800 +578 ln(n+1).
a. Vérifier que cette suite satisfait aux données du tableau précédent.
u0 = 800 +578 ln(1) = 800.
u7 = 800 +578 ln(7+1) ~2002.
b. On considère l’algorithme suivant :
S <-- 0
Pour i allant de 0 à 15
S <-- S +ARRONDI(800+578ln(1+i))
Fin pour.
On précise que ARRONDI (x) signifie : calculer la valeur arrondie de x à l’entier le plus proche.
Une fois l'algorithme exécuté, S contient la valeur 30 529. Interpréter ce résultat dans le contexte de l’exercice.
Entre 2001+15 =2016, l'usine a produit un total de 30 529 pales.
c. La suite (un) peut-elle modéliser la production des pales d'éoliennes de l'usine espagnole depuis 2001 ? Justifier la réponse.
Ce modèle convient.

|
|
2. On examine maintenant une modélisation de la production par la suite géométrique (vn) de premier terme v0= 800 et de raison q=1,14 .
a. Exprimer vn en fonction de n .
vn = 800 x 1,14n.
b. Calculer v7. On donnera le résultat arrondi à l’unité.
v7 = 800 x 1,147~2002.
c. On rappelle que la somme des premiers termes consécutifs d'une suite géométrique de premier terme v0 et de raison q est donnée par :
v0 x(1-qn+1) / (1-q).
Calculer v0 +v1 +...+v15. On donnera le résultat arrondi à l’unité.
800x(1-1,1416) /(1-1,14) ~40 784.
d. Peut-on modéliser par la suite (vn) la production, depuis 2001, de pales d’éoliennes de l’usine espagnole ? Justifier la réponse.
Non, 40784 diffère de 30 529.
Partie B.
L’entreprise gère aussi la réparation des pales sur leur lieu d'utilisation.
On estime que la durée de vie d’une pale, exprimée en années, avant la
première réparation, est une variable aléatoire X qui suit la loi
exponentielle de paramètre l= 0,125 .
Pour chaque question, donner le résultat arrondi à 10-3 .
1. Calculer P(0 < X < 5).
P(0 < X < 5) = 1 -e-0,125 x5 = 0,465.
2. Calculer la probabilité qu’une pale n'ait pas eu de réparation au cours des dix premières années.
P( X > 10) = 1-P( X < 10) = e-0,125 x10 = 0,287.
3. Déterminer la durée de vie moyenne d’une pale avant la première réparation.
1 / 0,125 = 8 ans.
Exercice 4. QCM.
1. Si z1 = -1 +i 3½ et z2 =eip/3 alors le quotient z1 / (z22) vaut.
a. : -2 ; b : -3½+i ; c : 2 ( vrai) ; d : -3½-i.
z2 = cos ( p/3) + i sin( p/3) =0,5(1 + i 3½ )
z22 = e i2p/3 = cos( 2p/3) + isin ( 2p/3) = 0,5(-1 +i 3½).
z1 / (z22) = 2 .
2. Si z1 = -1 +i 3½ et z2 =eip/3 alors le produit conjugué de z1 x z2 vaut. :
a : -2 ; b : 1-i 3½ ( vrai) ; c : eip ; d : -1-i 3½.
conjugué de z1 x z2 = (-1 -i 3½ ) x 0,5x (1 + i 3½ )= -0,5(1 + i 3½ )2 = -0,5(1+2 i 3½ -3) =1- i 3½.
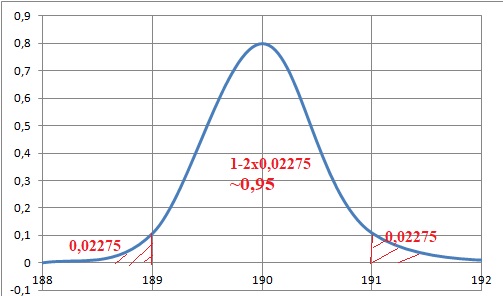
3. Soit X une variable aléatoire qui suit une loi normale d’espérance µ et d’écart-type s.
Sachant que P(X ∈ [189 ; 191] ~ 0,95 , µ et s peuvent prendre les valeurs :
a. 1 et 190 ; b. 190 et 1 ; c. 190 et 0,5 ( vrai) ; d. 0,5 et 190.
4. Dans le cadre du
fonctionnement correct d'une chaîne de production de pièces détachées,
la proportion de pièces détachées conformes doit être 96 %.
On contrôle la production de la chaîne en prélevant de manière aléatoire un échantillon de 150 pièces détachées.
On rappelle que l’intervalle de fluctuation asymptotique à 95 % de la
fréquence p des pièces détachées conformes sur un échantillon de taille
n est :
[p -1,96(p(1-p) / n)½ ; p +1,96(p(1-p) / n)½ ]
En utilisant un intervalle de fluctuation asymptotique à 95 %, on
prendra la décision d'effectuer des réglages sur la chaîne de
production si le nombre de pièces détachées
non conformes trouvées dans l’échantillon prélevé est :
a. 8 ; b. 9 ; c. 10 ; d. 11 (vrai).
1,96(p(1-p) / n)½ = 1,96 x(0,96 x0,04 / 150)½ = 0,03136.
[0,96 -0,03136 ; 0,96 +0,03136 ] soit [0,929 ; 0,991 ].
1- 8 / 150 = 0,947 appartient à l'intervalle.
1- 9 / 150 = 0,94 appartient à l'intervalle.
1- 10 / 150 = 0,933 appartient à l'intervalle.
1- 11 / 150 = 0,927 n'appartient pas à l'intervalle.
|
|