Mathématiques,
Bac Sti2d, STL, SPCL, Métropole 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice 1. QCM.
1. Le plan complexe est muni d’un repère. On considère le point A de coordonnées (-4*2½ ; 4*2½).
Une écriture exponentielle de l’affixe du point A est :
a. 8e-i3p/4 ; b.8ei3p/4 ( vrai) ; c. 4*2½e-i3p/4 ; d. 4*2½ei3p/4 .
OA = [(-4*2½)2 +(4*2½)2]½ = 8.
zA / 8 = -1/2½ + i /2½ = cos (3p/4) + i sin (3p/4).
2. Sur le graphique ci-dessous, l’aire grisée est délimitée par la courbe d’équation y = 2e-x , l’axe des abscisses et les droites d’équation x = a et x=2, où a est un nombre réel strictement inférieur à 2.
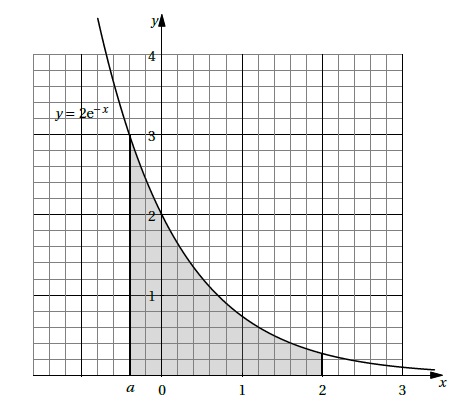
L’aire grisée a une valeur strictement comprise entre 0,5 et 1 unité d’aire lorsque a est égal à :
a. -0,5 ; b. 0 ; c. 0,5 ( vrai) ; d. 1,5.
3. On considère
l’équation différentielle y' +2y = 6 où y désigne une fonction
dérivable sur R. On note f l’unique solution de cette équation
différentielle vérifiant f (0) = 5.
La valeur de f (2) est :
a. 2e-4+3 ( vrai) ; b. 2e4+3 ; c. 5e-4+3 ; d. 5e4+3.
Solution générale de cette équation sans second membre f(x) =A e-2x.
Solution particulière de l'équation avec second membre : y = 3.
Solution générale de cette équation : f(x) = A e-2x +3.
f(0) = 5 = A+3 ; f(x) = 2 e-2x+3.
f(2) = 5 = 2 e-4+3.
4. On considère la fonction f définie sur ]0 ; Å1[ par f (x) = ln(x).
La primitive F de f sur ]0 ; +oo[ telle que F(1) = 3 est donnée par :
a. F(x)= x ln(x)-2x +5
b. F(x) = 3 / x
c. F(x) = x ln(x)+3
d. F(x) = x ln(x) -x+4. (Vrai).
a. On pose u = x et v = ln(x) ; u' = 1 et v' = 1 /x ; u'v +v'u =ln(x)+1
f '(x) =ln(x) +1-2 = ln(x)-1.
c. On pose u = x et v = ln(x) ; u' = 1 et v' = 1 /x ; u'v +v'u =ln(x)+1
f '(x) =ln(x) +1.
d. On pose u = x et v = ln(x) ; u' = 1 et v' = 1 /x ; u'v +v'u =ln(x)+1
f '(x) =ln(x) +1-1 = ln(x).
F1) = 1 ln(1)-1+4 = 3.
|
|
|
|
|
Exercice 2.
Après
son installation, un lundi matin, un aquarium contient 280 litres d’eau
et des poissons. Par évaporation, le volume d’eau dans l’aquarium
diminue de 2% par semaine. Compte tenu du nombre de poissons, cet
aquarium doit contenir en permanence au minimum 240 litres d’eau.
Partie A.
1. Quel volume d’eau restera-t-il dans l’aquarium au bout d’une semaine ?
280 x 0,98 = 274,4 L.
2. Est-il vrai qu’au bout de deux semaines, exactement 4% du volume d’eau initial se seront évaporés ? Justifier.
Au bout de deux semaines, il reste : 274,4x 0,98 = 268,912 L.
280 x0,96 = 268,8 L diffère de 268,912 L ; l'affirmation est fausse.
3. Déterminer au bout de combien de semaines le volume d’eau dans l’aquarium deviendra insuffisant.
280 x0,98n < 240 ; 0,98n < 240 /280 ;
n ln(0,98) < ln(240/280) ; n > ln(240/280) / ln(0,98). ; n ~7,6.
Au bout de 8 semaines, le volume d'eau est insuffisant..
Partie B.
On ajoute chaque lundi matin, en une seule fois, 5 litres d’eau pour compenser l’évaporation hebdomadaire de 2%.
On note u0 le volume initial d’eau en litres dans l’aquarium. Ainsi u0 = 280.
Pour tout entier naturel n supérieur ou égal à 1, on note un
le volume d’eau dans l’aquarium, en litres, n semaines après son
installation, immédiatement après l’ajout hebdomadaire des 5 litres
d’eau.
1. Vérifier que u2 = 278,812.
u1 = 280 x0,98 +5 =279,4 L.
u2 = 279,4 x0,98 +5 =278,812 L.
2. Justifier que pour tout entier naturel n, un+1 = 0,98un +5.
Chaque semaine on ajoute 5 L d'eau et il s'évapore 2 % du volume d'eau initial.
un+1 = 0,98un +5.
3. Montrer que la suite (un) n’est pas géométrique.
La suite serait géométrique si un+1 = 0,98un .
4. On considère l’algorithme ci-dessous dans lequel k désigne un nombre entier naturel et U un nombre réel.
U <-- 280
Pour k allant de 1 à 6.
U<-- U x 0,98 +5
Fin pour.
a. Recopier et compléter l’algorithme pour qu’à la fin de son exécution, la variable U contienne u6.
b. Quel est le volume d’eau dans l’aquarium, en litres à 10-2 près, 6 semaines après son installation immédiatement après l’ajout hebdomadaire des 5 litres d’eau.
Semaine n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
Volume d'eau (L), un
|
280
|
279,4
|
278,81
|
278,24
|
277,67
|
277,128
|
276,58
|
5. On considère la suite (vn) définie pour tout entier naturel n par vn = un - 250. On admet que la suite (vn) est une suite géométrique de raison 0,98.
a. Calculer v0.
v0 = u0-250 = 280-250 = 30.
b. Exprimer vn en fonction de n.
vn = v0 x0,98n.
c. En déduire que, pour tout entier naturel n, un = 30 x0,98n +250.
un = vn+ 250 = v0 x0,98n +250 = 30 x0,98n +250.
d. Justifier que la préconisation concernant le volume d’eau dans l’aquarium est respectée.
0 < 0,98 < 1, donc 0,98n tend vers zéro quand n tend vers plus l'infini.
un tend vers 250 quand n tend vers plus l'infini.
|
|
Exercice 3..
Le
niveau sonore N d’un bruit, à une distance D de sa source, dépend de la
puissance sonore P de la source. Il est donné par la relation
N = 120 + 4 ln (P / (13D2)).
où N est exprimé en décibels (dB), P enWatts (W) et D en mètres (m).
Partie A.
Les questions 1. et 2. sont indépendantes.
1. Calculer le
niveau sonore N d’un bruit entendu à 10 mètres de la source sonore dont
la puissance P est égale à 2,6 Watts. On arrondira le résultat à
l’unité.
N = 120 + 4 ln(2,6 / (13 x102)) = 95 dB.
2. On donne N = 84 dB et D= 10 m. Déterminer P. On arrondira le résultat à 10-2 près.
84 = 120 + 4 ln(P /1300) ; -36 = 4 ln(P/1300) ; -9 = ln(P /1300) ; P = 1300 e-9 = 0,16 W.
Partie B.
Une entreprise de travaux publics réalise un parking en plein air. Sur
le chantier d’aménagement de ce parking, une machine de découpe a une
puissance sonore P égale à 0,026 Watts.
1. a. Montrer qu’à une distance D de la machine, le niveau sonore N dû à celle-ci vérifie la relation :
N = 120+4ln(0,002) - 4ln(D2).
N = 120 + 4 ln (P / (13D2)) = 120 +4 ln(0,026 / 13) - 4 ln(D2).
N = 120 + 4 ln(0,002) -4 ln(D2).
b. Montrer qu’une approximation de N peut être 95,14-8ln(D).
N = 120 + 4 ln(0,002) -4x2 ln(D).
N ~ 120 -24,858 -8 ln(D).
N ~95,14-8ln(D).
Dans la suite de
l’exercice, à une distance de x mètres de la machine, le niveau sonore
N émis par la machine est modélisé par la fonction f définie sur
l’intervalle [0,1; 20] par : f (x) = 95,14-8ln(x).
2. a. Déterminer une expression de f '(x), où ' désigne la fonction dérivée de f .
f ' = -8 / x.
b. Donner le signe de f '(x) pour tout x de l’intervalle [0,1; 20].
f ' (x) est négative sur l’intervalle [0,1; 20].
c. En déduire le sens de variation de la fonction f sur l’intervalle [0,1 ; 20].
f(x) est strictement décroissante sur l’intervalle [0,1; 20].
3.
On suppose qu’un ouvrier de cette entreprise se situe à trois mètres de
la machine. La législation en vigueur l’oblige à porter des protections
individuelles contre le bruit dès qu’un risque apparaît.
Justifier que l’ouvrier doit porter des protections individuelles contre le bruit.
N = 95,14 -8 ln(3) ~ 86,35 dB.
Cette valeur étant comprise entre 85 et 90 dB, ( risque faible) l'ouvrier doit porter des protections contre le bruit.
4. Déterminer à quelle distance de la machine un ouvrier de l’entreprise sort de la zone
de risque élevé (c’est-à-dire lorsque le niveau sonore est inférieur à 90 dB).
95,14 -8 ln(D) < 90 ; 8 ln(D) > 95,14 -90 ; ln (D) > 5,14 / 8 ; ln (D ) > 0,6425 ; D > 1,91 m.
Partie C.
On s’intéresse au lien entre la puissance P d’un bruit et la distance D
de sa source pour différentes valeurs de son niveau sonore N.
On admet que pour une puissance de 0,02 Watt, le niveau sonore du bruit
est de 74,9 décibels à une distance de 11 mètres de la source sonore.
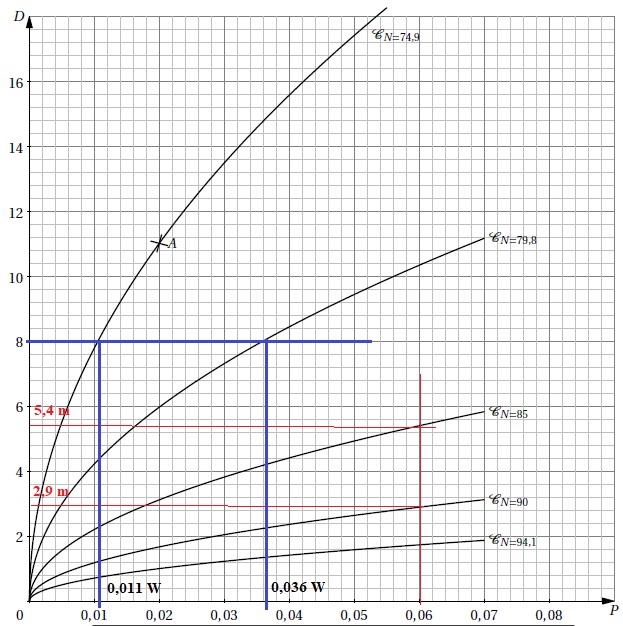
Ainsi, le point A de coordonnées (0,02; 11) appartient à la courbe CN=74,9.
1. Pour un bruit de
puissance P égale à 0,06 W, déterminer graphiquement à quelles
distances minimale et maximale de la source peut se situer une personne
pour que le niveau sonore N soit compris entre 85 et 90 dB.
2. Pour une source
sonore située à une distance D de 8 m, déterminer graphiquement les
puissances minimale et maximale de cette source pour obtenir un niveau
sonore compris entre 74,9 dB et 79,8 dB.
Exercice 4.
Un industriel commercialise des portes blindées. Il projette de lancer
un nouveau modèle deportes blindées : les portes « SECUR ». Équipées
d’un digicode et d’une caméra, elles serontdonc plus sécurisées que
celles déjà existantes sur le marché.
Les résultats seront arrondis à 10-4 près.
Partie A.
Avant de débuter son projet, l’industriel s’intéresse à une étude
portant sur le prix de vente des portes blindées classiques existantes.
Le prix de vente, en euros, d’une porte blindée classique est une
variable aléatoire X qui suit la loi normale d’espérance µ= 3000 et
d’écart type s= 750.
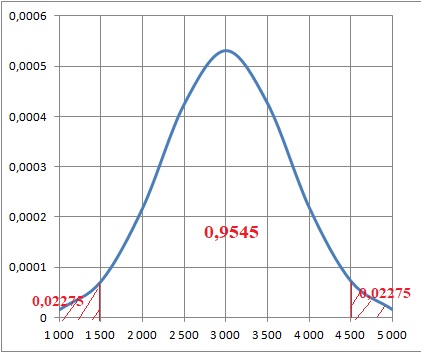
1. Déterminer la probabilité P(1500 < X < 4500).
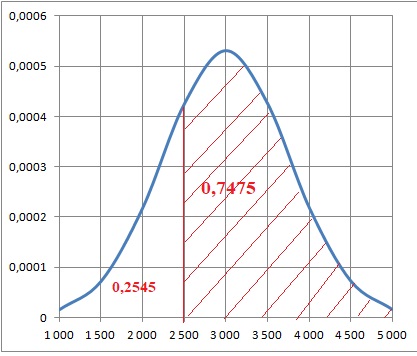
2. Déterminer la probabilité qu’une porte blindée classique coûte plus de 2500 euros.
3. a. Recopier et compléter le tableau suivant où a désigne un nombre entier naturel.
n
|
P(X) < a
|
3950
|
0,8974
|
3960
|
0,8997
|
3961
|
0,9000
|
3964
|
0,9006
|
3965
|
0,9009
|
3966
|
0,9011
|
3970
|
0,9021
|
b.
Déterminer le montant minimal, à l’euro près, tel qu’au moins 90% des
portes blindées classiques aient un prix de vente inférieur à ce
montant.
3961 €.
c. L’industriel
estime que le prix de vente du modèle de porte blindée équipée « SECUR
» ne devra pas dépasser de plus de 15% le montant minimal précédent.
Quel prix de vente maximal M, à l’euro près, peut-il envisager pour une
porte du modèle « SECUR » ?
3961 x 1,15 ~4555 €.
Partie B.
L’industriel envisage de commercialiser les portes blindées de modèle «
SECUR » au tarif M déterminé précédemment. Il souhaite estimer la
proportion de personnes susceptibles d’acheter son nouveau modèle. Une
enquête est réalisée sur un échantillon de 984 personnes intéressées
par l’achat d’une porte blindée. Sur cet échantillon, 123 personnes se
disent favorables à l’achat du modèle « SECUR ».
1. Déterminer
l’intervalle de confiance, au niveau de confiance 95%, de la proportion
de personnes favorables à l’achat du nouveau modèle.
On rappelle que pour une fréquence f observée dans un échantillon de
taille n, l’intervalle de confiance au niveau de confiance 95% de la
proportion p du caractère étudié dans la population est donné par :
[f-1,96(f(1-f) / n)½ ; f+1,96(f(1-f) / n)½ ]
f = 123 / 984 = 0,125 ; 1 -f = 0,875.
1,96 (0,125 x 0,875 / 984)½ = 0,0207 ;
[0,125 -0,0207 ; 0,125 +0,0207 ] soit [0,104 ; 0,146 ].
2. Pour que
l’industriel prenne le risque d’investir dans les portes « SECUR », il
faudrait qu’au minimum 20% des personnes souhaitant s’équiper d’une
porte blindée soient favorables à ce nouveau modèle. A-t-il intérêt à
réaliser son projet ?
Non, 0,20 n'appartient pas à l'intervalle [0,104 ; 0,146 ].
|
|