Mathématiques,
bac ST2S Nlle Calédonie 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1.6 points.
Des études statistiques ont prouvé que 4% de la population d’un pays est atteinte par une certaine maladie.
Pour cette maladie, un laboratoire pharmaceutique élabore un nouveau test de dépistage.
Les essais sur un groupe témoin ont donné les résultats suivants :
• 4% des individus du groupe témoin sont atteints par la maladie;
• 85% des personnes atteintes par la maladie réagissent positivement au test ;
• 99% des personnes non atteintes par la maladie réagissent négativement au test.
On choisit au hasard un individu dans le groupe témoin; on admet que chaque individu a la même probabilité d’être choisi.
Pour tout évènement E, on note non E l’évènement contraire de E.
Si F est un évènement de probabilité non nulle, la probabilité de E sachant F est notée PF (E).
On note les évènements suivants :
• M : « l’individu choisi est atteint par la maladie » ;
• T : « l’individu choisi réagit positivement au test ».
1. Déterminer la probabilité de l’évènement M.
P(M) = 0,04.
2. Déterminer la probabilité qu’un individu réagisse positivement au test sachant qu’il est atteint par la maladie.
PM(T) = 0,85.
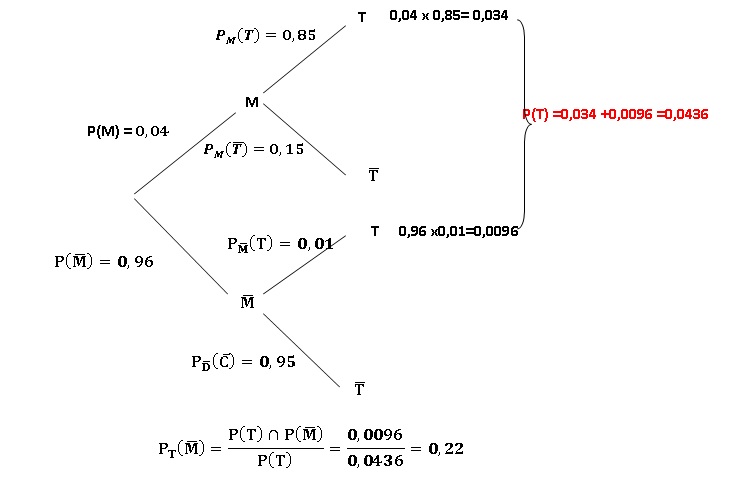
3. Recopier et compléter l’arbre de probabilité ci-dessous.
4. Définir par une phrase l’évènement M ∩T puis calculer sa probabilité.
La personne atteinte par la maladie réagit positivement au test.
P(M n T)= 0,04 x0,85 = 0,034.
5. Montrer que la probabilité de l’évènement T est égale à 0,0436.
6. Calculer la
probabilité qu’un individu ne soit pas atteint par la maladie sachant
qu’il réagit positivement au test. Arrondir le résultat au centième.
7.
Certains organismes de santé autorisent la commercialisation d’un test
de dépistage lorsque la probabilité de ne pas être atteint par la
maladie sachant que la réaction au test est positive est inférieure à
20%.
Le laboratoire pharmaceutique peut-il espérer, selon ce critère, une commercialisation de son test ?
Non, 22 % des individus non malade réagissent positivement au test.
|
...
|
|
Exercice 2. 8 points.
L’Allocation
Personnalisée d’Autonomie en établissement (APA en établissement) est
une allocation destinée aux personnes âgées de plus de 60 ans en perte
d’autonomie et résidant dans un établissement de santé.
Dans cet exercice, on modélise de deux façons différentes l’évolution
du montant de l’APA en établissement dans un département français.
Partie A.
Le tableau suivant donne les montants, en euro, de l’APA en établissement de 2007 à 2015 pour le département considéré :

On a représenté, dans un repère orthogonal, le nuage de points de coordonnées (xi ; yi ) associé à cette série statistique.
1. a. Déterminer les coordonnées du point moyen G de ce nuage de points. Arrondir l’ordonnée à l’unité.
b. Placer le point G dans le repère précédent.
xmoyen =(1 +2 +3 +4 +5 +6 +7 +8 +9 )/ 9 =5.
ymoyen =(13504 +14443 +14914 +15351 +15751 +16144 +16744 +17190 +18070) / 9 =15790 €.
2. On admet que la droite D d’équation y = 516x +13210 réalise un bon ajustement affine du nuage de points jusqu’en 2020.
a. Tracer la droite D dans le repère précédent.Donner les coordonnées des points choisis pour la tracer.
(0 ; 13210) et G(5 ; 15790).
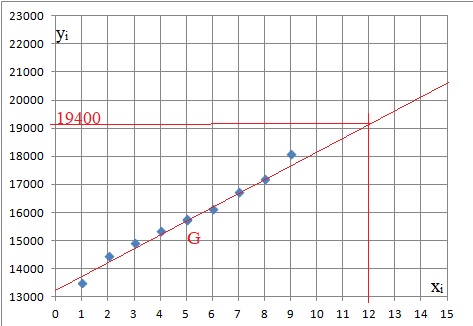
b. À l’aide de cet ajustement, donner une estimation du montant de l’APA en établissement dans ce département pour l’année 2018.
x = 12 ; y = 516 x12 + 13210 =19402 €.
Partie B :
On a recopié le tableau précédent dans une feuille de calcul d’un tableur.
Les cellules de la ligne 4 sont au format pourcentage.
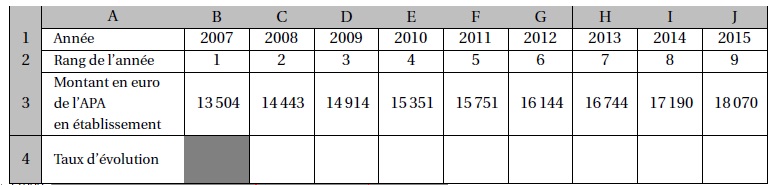
1. a.
Calculer le taux d’évolution du montant de l’APA en établissement dans
ce département entre 2014 et 2015. Arrondir le résultat à 0,1%.
(18070 -17190) / 17190 x100 =5,1 %.
b. Quelle formule
doit-on entrer dans la case C4 pour obtenir, par recopie vers la
droite, les taux d’évolution en pourcentage du montant de l’APA en
établissement dans ce
département, entre deux années consécutives ?
=(C3-B3)/B3
2. On suppose
maintenant que le montant de l’APA en établissement dans ce département
augmente de 5,1% par an après 2015. On décide de modéliser ce montant
par une suitenumérique (un).
Pour tout entier naturel n, un désigne le montant de l’APA en
établissement dans ce département, en euro, pour l’année (2015+n).
Ainsi, u0 = 18070.
a. Calculer u1. Arrondir le résultat à l’unité. Interpréter la valeur de u1 dans le contexte de l’exercice.
18070 x 1,051 =18992 €.
En 2016, le montant de l'APA sera de 18 992 €.
b. Donner, sans justification, la nature de la suite (un) et sa raison.
Suite géométrique de raison 1,051.
c. Exprimer, pour tout entier naturel n, un en fonction de n.
un = 18070 x1,051n.
3. Parmi les deux modèles (l’ajustement affine de la partie A et la suite (un) de la partie B), quel est celui qui prévoit le plus haut montant de l’APA en établissement pour l’année 2018?
En 2018, n = 3 ; u3 = 18070 x 1,0513 =20 978 €. Ce modèle de la suite conduit au montant le plus élevé.
|
....
|
Exercice 3. 6 points.
Partie A.
Soit f la fonction définie sur R par : f (t ) = −t 3 +3t 2 +24t +28.
Soit f ′ la fonction dérivée de la fonction f .
1. Calculer f ′(t ).
f '(t) = -3t2 +6t +24.
2. Montrer que, pour tout t appartenant à R, f ′(t )= (4−t ) (3t +6).
(4-t)(3t+6) = 12t +24 -3t2 -6t = -3t2 +6t +24.
3. Étudier le signe de f ′(t ).
4. En déduire le tableau de variation de la fonction f sur R.
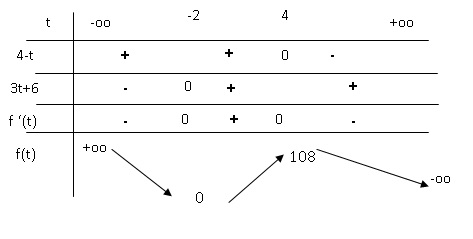
Partie B.
Une épidémie de varicelle s’est déclarée dans les crèches d’une commune. On observe son évolution dans le temps.
Un relevé hebdomadaire effectué par le service communal d’hygiène et de santé a permis d’établir le tableau suivant :
Nombre de semaines écoulées
depuis le début de l'épidémie (xi)
|
0
|
1
|
2
|
3
|
4
|
5
|
Nombre de cas de varicelle ( yi)
|
25
|
52
|
82
|
100
|
110
|
97
|
1. a. On a
représenté, dans un repère orthogonal, une partie de la courbe
représentative de la fonction f . Dans ce repère, placer les points de
coordonnées (xi ; yi ) correspondant au relevé ci-dessus.
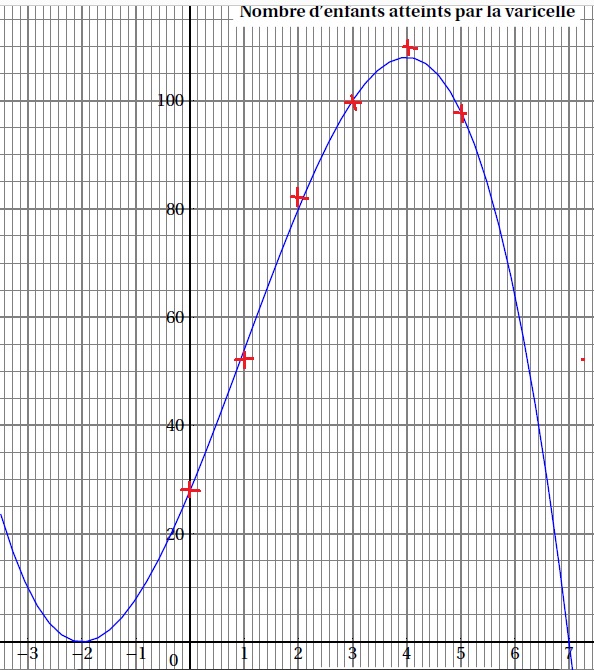
b. Expliquer en
quoi il est pertinent de modéliser le nombre de cas de varicelles au
cours du temps par la fonction f . Préciser sur quel intervalle.
Sur l'intervalle [0 ; 7 ] la fonction donne une évolution précise du nombre de cas de varicelle.
|
.
2. En utilisant cette modélisation et avec la précision permise par le graphique, déterminer :
a. le nombre d’enfants atteints par la varicelle au bout de 10 jours (on laissera apparents les traits permettant la lecture) ;
b. la période durant laquelle
le nombre de cas de varicelle est supérieur à 100. Arrondir au jour (on
laissera apparents les traits permettant la lecture).
3. D’après ce modèle, au bout
de combien de semaines n’y aura-t-il plus aucun enfant atteint de
varicelle dans les crèches de la commune? Justifier la réponse.
Au bout de 7 semaines ( f (t) = 0) , il n'y a plus d'enfant atteint de varicelle.
|
|