Mathématiques,
Bac St2S Métropole 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1. (6 points)
La
loi de financement de la Sécurité sociale comprend un objectif national
de dépenses d’assurance maladie, qui est voté chaque année par le
Parlement.
Le montant des dépenses d’assurance maladie a été évalué pour l’année
2016 à 185,2 milliards d’euros. Le Parlement a voté une croissance de
ces dépenses de 2,1% pour l’année 2017.
1. Montrer que le
montant des dépenses d’assurance maladie voté pour l’année 2017 est de
189,1 milliards d’euros (à cent millions près).
185,2 x (1+0,021) =189,1.
Pour
estimer les montants des années suivantes, on suppose que le Parlement
votera chaque année une augmentation de 2,1% de ces dépenses.
On modélise à l’aide d’une suite (vn) le montant, en milliards d’euros, des dépenses d’assurance maladie voté chaque année. On note v0 lemontant voté pour l’année 2016 et vn le montant voté pour l’année (2016+n), où n est un entier positif ou nul.
On a ainsi v0 = 185,2.
On veut utiliser la feuille de calcul automatisé ci-dessous afin d’obtenir les valeurs successives de la suite (vn).
|
A
|
B
|
1
|
n
|
vn
|
2
|
0
|
185,2
|
3
|
1
|
189,1
|
4
|
2
|
|
5
|
3
|
|
2. Quelle formule
peut-on entrer dans la cellule B3 de sorte que, recopiée vers le bas,
elle permette d’afficher les valeurs de la suite (vn) ?
=B2*1,021
3. Indiquer sans justification la nature de la suite (vn). Donner la valeur de sa raison.
Suite géométrique de raison 1,021 et de premier terme v0 =185,2.
4. Exprimer vn en fonction de n.
vn = 185,2 x1,021n.
5. Déterminer une
estimation dumontant des dépenses d’assurance maladie voté par le
Parlement pour l’année 2020. (Arrondir la valeur à la centaine de
millions.).
En 2020, n = 4 ; v4 = 185,2 x1,0214 =201,3.
6. Résoudre, dans l’ensemble des nombres réels, l’inéquation 185,2x1,021x >210.
ln(185,2) + x ln(1,021) > ln(210) ; x > [ln(210)-ln(185,2) ] / ln(1,021) ; x > 6,046.
7. Déterminer,
suivant ce modèle, l’année pour laquelle sera voté, pour la première
fois, un montant de dépenses d’assurance maladie supérieur à 210
milliards d’euros.
n = 7 , année 2023.
|
|
|
|
|
Exercice 2. 8 points.
Un
laboratoire prévoit de commercialiser un nouveau capteur destiné à
améliorer le suivi en continu de la glycémie des diabétiques.
Ce laboratoire a demandé à un service hospitalier de proposer ce
capteur à plusieurs patients afin de déterminer son influence sur
l’équilibre du diabète.
Les deux parties de cet exercice peuvent être traitées de manière indépendante.
Partie A : Influence du capteur
À la fin de l’évaluation par le service hospitalier, l’étude de
l’ensemble des dossiers des patients diabétiques a permis d’établir que
:
• 65% des patients ont un diabète équilibré;
• parmi les patients qui ont un diabète équilibré, 26% étaient équipés du capteur de glycémie en continu;
• parmi les patients qui ont un diabète déséquilibré, 12% étaient équipés du capteur de glycémie en continu.
On choisit au hasard le dossier d’un patient et on considère les évènements suivants :
• E : « le dossier est celui d’un patient dont le diabète est équilibré » ;
• C : « le dossier est celui d’un patient équipé du capteur de glycémie en continu » ;
1. Déterminer la probabilité de l’évènement E, notée p(E).
p(E) = 0,65.
2. Déterminer la probabilité de PE (C), probabilité de C sachant E..
PE (C)=0,26.
3. Recopier et compléter l’arbre pondéré suivant :
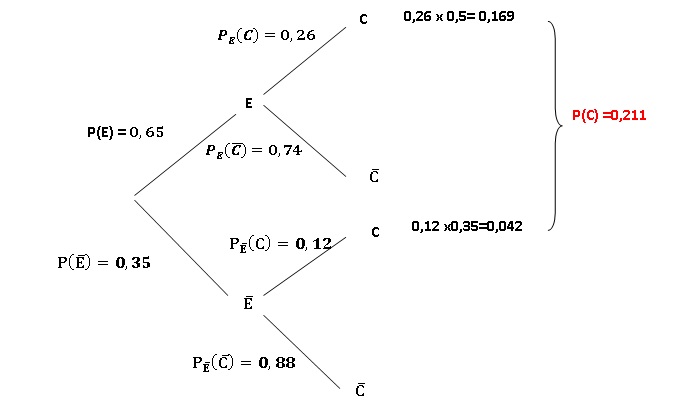
4. Les résultats seront arrondis au millième.
a. Décrire par une phrase l’évènement E n C. Calculer la probabilité de cet évènement.
E n C = 0,65 x0,26 = 0,169.
Le patient a un diabète équilibré et il est équipé d'un capteur de glycémie en continu.
b. Montrer que la valeur de P (C) est égale à 0,211. Interpréter ce résultat dans le contexte de l’exercice.
P(C) = 0,26 x0,65 + 0,35 x0,12 = 0,169 + 0,042 = 0,211.
211 patients diabétiques sur 1000 sont équipés d'un capteur de diabète en continu.
c. En déduire la
probabilité que le dossier choisi soit celui d’un patient dont le
diabète est équilibré sachant que celui-ci est équipé du capteur de
glycémie en continu.
PC(E) =P(C n E) / P(C) = 0,169 / 0,211 = 0,801.
5. L’objectif du laboratoire est que son capteur permette de diviser par deux la probabilité d’avoir un diabète déséquilibré.
On admet que la probabilité qu’un patient non équipé d’un capteur de
glycémie en continu présente un diabète déséquilibré est environ égale
à 39%.
Peut-on considérer que l’objectif du laboratoire est atteint ?
P(non C) = 1-0,211 = 0,789.
P(non E) = 0,35.
Pnon C ( non E ) = P(non E n non C) = P(non C) = 0,88 x 0,35 / 0,789 = 0,39. Objectif atteint.
Partie B : Fiabilité du capteur
Un service hospitalier reçoit six capteurs de glycémie en continu dont
il souhaite vérifier la fiabilité. Il en équipe six patients. Pour
chacun d’eux, il effectue un test sanguin qui permet de mesurer le
pourcentage x d’hémoglobine exposée au glucose.
Ce pourcentage x est comparé à la moyenne y des glycémies mesurées, en mmol. L −1, par le capteur au cours des trois mois d’étude. Dans la suite du problème, le nombre y est appelé glycémie moyenne du capteur.
Les résultats sont regroupés dans le tableau suivant :
Patient
|
A
|
B
|
C
|
D
|
E
|
F
|
x (%)
|
6,4
|
7,8
|
9,3
|
6,9
|
7,3
|
8,3
|
y ( mmol / L)
|
7,6
|
9,8
|
11,1
|
8,2
|
9,2
|
10,7
|
La notice technique du capteur indique que, lorsque le capteur est fiable, les mesures obtenues sont liées par la relation :
y = 1,6x −2,6.
1. D’après la
relation précédente, quelle devrait être la glycémie moyenne d’un
capteur fiable si le test sanguin donne une valeur x égale à 8 ?
y = 1,6 * 8 -2,6 = 10,2.
2. Tracer dans le
repère fourni en annexe la droite d’équation : y = 1,6x −2,6. On
précisera les coordonnées des points utilisés.
(x = 6 ; y =7) et ( x = 9 ; y = 11,8).
3. a. Placer, dans le repère fourni, les points qui correspondent aux 6 patients.
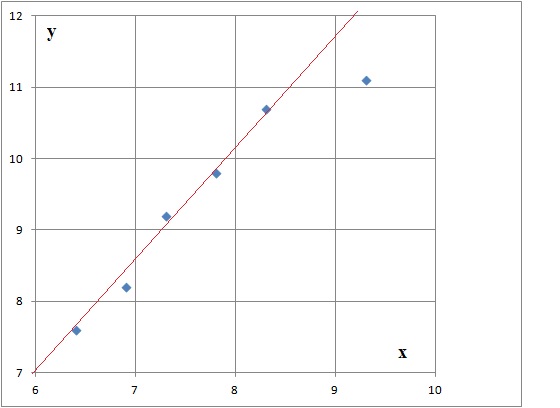
Au vu de ces
résultats, le service hospitalier pense que l’un des capteurs n’a pas
permis d’obtenir des résultats fiables. Quel patient est concerné par
ce problème ?
Pour le patient F, le point figuratif est très éloigné de la droite.
|
|
Exercice 3. 6 points.
Dans
un milieu de culture, une population bactérienne évolue en fonction du
temps t exprimé en heures. À l’instant t = 0, il y a 10 000 bactéries
dans la culture. À l’instant t0, on y introduit un puissant antibiotique.
Le graphique ci-dessous donne l’évolution du nombre de bactéries
(exprimé en dizaines de milliers) en fonction du temps t (en heures).
Partie A : Étude graphique
1. Remettre les
cinq phrases qui suivent dans le bon ordre afin qu’elles décrivent les
étapes successives de l’évolution au cours du temps du nombre de
bactéries observées sur le graphique précédent.
La réponse sera donnée sous la forme d’une suite de cinq lettres, par exemple « a-d-b-c-e ».
a. Le nombre de bactéries augmente de moins en moins vite.
b. Le nombre de bactéries diminue de moins en moins vite.
c. Le nombre de bactéries diminue de plus en plus vite.
d. Le nombre de bactéries augmente de plus en plus vite.
e. On introduit la dose d’antibiotique.
d - e - a - c - b.
2. Déterminer, avec la précision permise par le graphique (tracer les pointillés nécessaires à la lecture) :
a. une estimation du nombre de bactéries au moment de l’introduction de l’antibiotique ;
b. une estimation du nombre maximum de bactéries obtenu dans ce milieu de culture ;
c. une estimation de l’instant à partir duquel le nombre de bactéries est inférieur à 5 000.
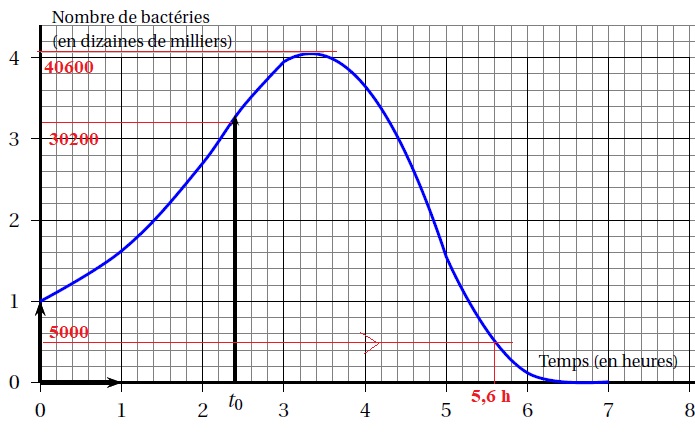
Partie B : Détermination du nombre maximal de bactéries
Entre 3 h et 5 h après le début de l’étude, le nombre de bactéries
(exprimé en dizaines de milliers), est donné en fonction de t (en
heures) par :
f (t ) = −0,9t 2 +6t −5,95.
1. Calculer l’image de 4,5 par la fonction f . Interpréter le résultat obtenu.
f(4,5) = -0,9 x4,52 +6 x4,5 -5,95 = -18,225 +27 -5,95 = 2,825.
2. Calculer f ′(t ) pour t appartenant à [3; 5] où f ′ désigne la fonction dérivée de f .
f '(t) = -2 x0,9 t +6 = -1,8 t +6.
3. Résoudre l’inéquation f ′(t ) > 0 dans l’intervalle [3; 5].
En déduire que f admet un maximum sur [3; 5] atteint pour t =10 / 3 = 6 / 1,8.
-1,8 t +6 >0 ; 1,8 t < 6 ; t < 6 / 1,8. (6 /1,8= 1 /0,3 = 10 / 3).
Si t < 6 /1,8 f '(t) est positive et f(t) est strictement croissante.
Si f '(t) = 6 /,18, f ' (t) est nulle.
Si t > 6 /1,8 f '(t) est négative et f(t) est strictement décroissante.
f(t) admet un maximum pour t = 6 / 1,8.
4. L’introduction de l’antibiotique a-t-elle permis d’éviter que le nombre de bactéries n’atteigne 40 000 ? Justifier.
f( 6 / 1,8) = -0,9 *(6 /1,8)2 +6 *6 / 1,8 -5,95 = -10 +20 -5,95 =4,05 ( soit 40 500 bactéries).
L'introduction de l'antibiotique n'a pas permis d'éviter que le nombre de bactéries n'atteigne 40 000.
|
|