Mathématiques, fonction, probabilités, Bac S Asie 2018

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .
.
.


Exercice 1.
Dans les parties A et B de cet exercice, on considère une maladie; tout individu a une probabilité égale à 0,15 d’être touché par cette maladie.
Partie A.
Cette partie est un questionnaire à choix multiples (Q. C. M.). Pour chacune des questions, une seule
des quatre réponses est exacte.  Aucune justification n’est demandée.
Un test de dépistage de cette maladie a été mis au point. Si l’individu est malade, dans 94% des cas le test est positif. Pour un individu choisi au hasard dans cette population, la probabilité que le test soit positif vaut 0,158.
1. On teste un individu choisi au hasard dans la population : le test est positif. Une valeur arrondie au centième de la probabilité que la personne soit malade est égale à : A : 0,94 ; B : 1 ; C : 0,89 (vrai) ; D : on ne peut pas savoir.
On définit les évènements : M " être malade" et T " test positif".

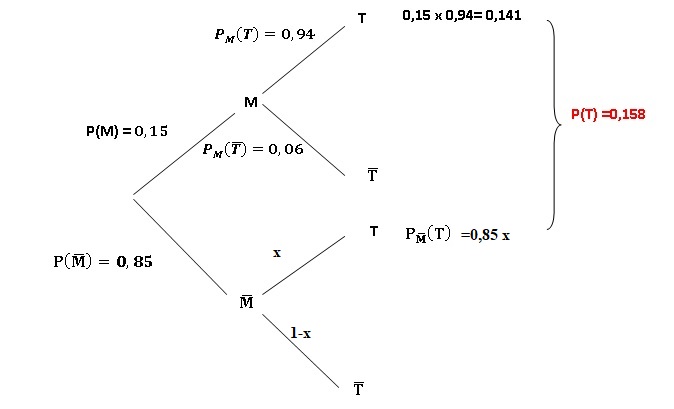
Probabilité qu'un individu malade soit testé positivement : 0,94 x0,15 = 0,141.
P test positif ( personne malade) =0,141 / 0,158~0,89.

2. On prélève un échantillon aléatoire dans la population, et on fait passer le test aux individus de cet échantillon. On souhaite que la probabilité qu’au moins un individu soit testé positivement soit supérieure ou égale à 0,99. La taille minimum de l’échantillon doit être égale à :
A : 26 personnes ;  B : 27 personnes ( vrai).; C : 3 personnes ; D : 7 personnes.
La population est assez importante pour que les n épreuves soient indépendantes de Bernoulli.
p =0,158 ; 1-p = 1-0,158 = 0,842.
Probabilité qu'aucun individu ne soit testé positivement : 0,842n.
Probabilité qu'au moins un individu soit testé positivement  : 1-0,842n > 0,99.
0,842n < 0,01 ; n > ln(0,01) / ln(0,842) ; n > 26,77.

3. Un vaccin pour lutter contre cette maladie a été mis au point. II est fabriqué par une entreprise sous forme de dose injectable par seringue. Le volume V (exprimé en millilitre) d’une dose suit une loi normale d’espérance μ = 2 et d’écart-type s. La probabilité que le volume d’une dose,
exprimé en millilitre, soit compris entre 1,99 et 2,01 millilitres est égale à 0,997.
La valeur de s doit vérifier :
A : s= 0,02;  B : s < 0,003 ; C : s > 0,003 ( vrai) ; D : s = 0,003.

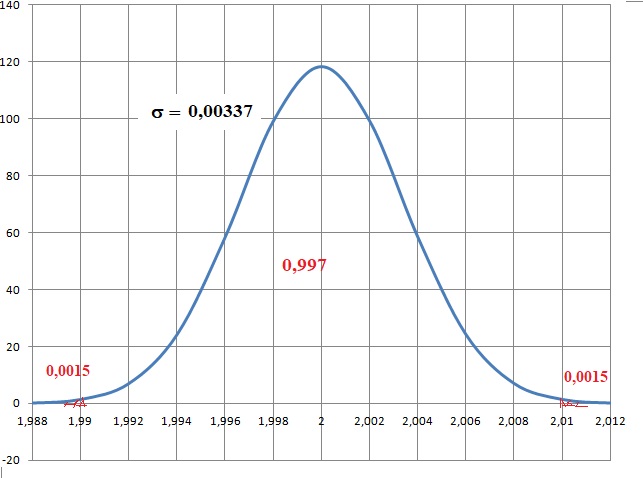Autre méthode : P(2-3s < X < 2+3s ~ 0,997.
0,01 = 3s ; s =0,01 / 3~0,0033.
Partie B.
1. Une boîte d’un certain médicament permet de soigner un malade.
La durée d’efficacité (exprimée en mois) de ce médicament est modélisée de la manière suivante ::
— durant les 12 premiers mois après fabrication, on est certain qu’il demeure efficace ;
— au-delà, sa durée d’efficacité restante suit une loi exponentielle de paramètre l.
La probabilité que l’une des boîtes prise au hasard dans un stock ait une durée d’efficacité totale supérieure à 18 mois est égale à 0,887.
Quelle est la valeur moyenne de la durée d’efficacité totale de ce médicament ?
On note E la variable aléatoire donnant la durée d'efficacité du médicament.
P(E > 18-12) = P(E> 6) = 0,887 = e-6l ;
ln 0,887 = -6 l ; l =0,019985.
Moyenne : 1 / l = 1 /0,019985 ~ 50.
2. Une ville de 100 000 habitants veut constituer un stock de ces boîtes afin de soigner les personnes malades.
Quelle doit être la taille minimale de ce stock pour que la probabilité qu’il suffise à soigner tous les malades de cette ville soit supérieure à 95% ?
n = 100 000 ; p = 0,15.
n > 30 ; np = 0,15 x 100 000 = 150000 > 5 ; n(1-p) =100 000 x0,85 = 85 000 > 5.
Les conditions sont requises pour calculer un intervalle de fluctuation asymptotique.
1,96 (0,15 x0,85 /100 000 )½ ~ 0,0022.
[0,15 -0,0022 ; 0,15 +0,0022] soit : [0,1478 ; 0,1522].
0,1522 x 100 000 = 15220 boîtes.

Exercice 1.
Une ferme aquatique exploite une population de crevettes qui évolue en fonction de la reproduction naturelle et des prélèvements effectués.
La masse initiale de celte population de crevettes est estimée à 100 tonnes.
Compte tenu des conditions de reproduction et de prélèvement, on modélise la masse de la population de crevettes, exprimée en tonne, en fonction du temps, exprimé en semaine, par la fonction fP , définie sur l’intervalle [0 ; +∞[ par :
fP (t ) = 100p /(1−(1−p)e−pt)
où p est un paramètre strictement compris entre 0 et 1 et qui dépend des différentes conditions de vie et d’exploitation des crevettes.
1. Cohérence du modèle
a. Calculer fP (0).
 fP (0) = 100.
b. On rappelle que 0 < p < 1.
Démontrer que pour tout nombre réel t >0, 1−(1−p)e−pt > p.
0 < p < 1 ; -p < 0 < 1-p.
Sur [ 0 ; +oo[, la fonction e-pt est strictement décroissante de 1 à 0.
e-pt < 1 ; (1-p) e-pt < 1-p.
-(1-p) e-pt > p-1.
1-(1-p) e-pt > p.
c. En déduire que pour tout nombre réel t >0, 0 < fP (t ) < 100.
1 / (1−(1−p)e−pt) <  1 / p.
Multiplier chaque membre par 100 p ;
100p / (1−(1−p)e−pt) <  100 soit fP (t ) < 100.
2. Étude de l’évolution lorsque p = 0,9.
Dans cette question, on prend p = 0,9 et on étudie la fonction f0.9 définie sur [0 ; +∞[ par :
f0,9(t )= 90 /(1−0,1e−0,9t) .
a. Déterminer les variations de la fonction f0.9.
On pose u=90 ; v = 1−0,1e−0,9t ; u' =0 ; v'= 0,09e−0,9t ;
f '0,9(t )=(u'v -v'u) / v2 = -90 x0,09e−0,9t / (1−0,1e−0,9t)2.
e−0,9t étant positif, f '0,9(t ) est négative et f0.9 est strictement décroissante sur [0 ; +∞[ .
b. Démontrer pour tout nombre réel t >0, f0,9(t )>90.
 f0,9(0) =100.
Quand t tend vers l'infini, e−0,9t tend vers zéro et f0,9(t ) tend vers 90.
c. Interpréter les résultats des questions 2. a. et 2. b. dans le contexte.
La masse de  crevettes diminue de 100 t à 90 t.






3. Retour au cas général
On rappelle que 0< p < 1.
Exprimer en fonction de p la limite de fP lorsque t tend vers +∞.
 Quand t  tend vers plus l'infini, le terme en exponentielle e−pttend vers zéro.
 fP (t ) tend vers 100p.
4. Dans cette question, on prend p =0,5.
a. Montrer que la fonction H définie sur l’intervalle [0 ; +∞[ par :
H(t ) =100ln(2−e-0,5t)+50t
est une primitive de la fonction f1/2 sur cet intervalle.
On pose u = 2−e-0,5t ; u' = 0,5e-0,5t ;
H '(t) = 100 x 0,5e-0,5t / (2−e-0,5t) +50.
H '(t) = [50e-0,5t +50((2−e-0,5t)] / (2−e-0,5t).
H '(t) =100 / (2−e-0,5t) =50 / (1-0,5 e-0,5t)= f0,5.
b. En déduire la masse moyenne de crevettes lors des 5 premières semaines d’exploitation,
c’est-à-dire la valeur moyenne de la fonction f1/2 sur l’intervalle [0; 5].
En donner une valeur approchée arrondie à la tonne.
Moyenne = [H(5) - H(0) ]/ 5 .
H(5) = 100 ln(2−e-2,5)+50 x5=  100 ln(2−e-2,5)+250 ;
H(0) = 0.
Moyenne = 20 ln(2−e-2,5)+50 ~63 tonnes.