Mathématiques,
volume d'une ampoule, suite,
Bac S Polynésie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
2.
Partie A -Modélisation de la forme de l’ampoule
Le plan est muni d’un repère orthonormé
On considère les points A(-1 ; 1), B(0 ; 1), C(4 ; 3), D(7 ; 0), E(4 ; -3), F(0 ; -1) et G(-1 ; -1).
On modélise la section de l’ampoule par un plan passant par son axe de révolution à l’aide de la figure ci-dessous :
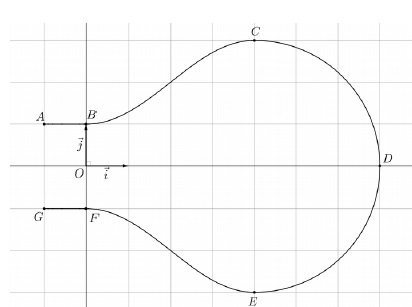
La partie de la courbe située au-dessus de l’axe des abscisses se décompose de la manière suivante :
• la portion située entre les points A et B est la représentation
graphique de la fonction constante h définie sur l’intervalle [-1 ; 0]
par h(x) = 1 ;
• la portion située entre les points B et C est la représentation
graphique d’une fonction f définie sur l’intervalle [0 ; 4] par f (x) =
a + b sin (c+px/4), où a, b et c sont des réels non nuls fixés et où le réel c appartient à l’intervalle [0 ; 0,5p].
• la portion située entre les points C et D est un quart de cercle de diamètre [CE].
La partie de la courbe située en-dessous de l’axe des abscisses est obtenue par symétrie par rapport à l’axe des abscisses.
1.a) On appelle f ' la fonction dérivée de la fonction f. Pour tout réel x de l’intervalle [0 ; 4], déterminer f '(x).
f '(x) =b p/4cos (c+px/4)
b)
On impose que les tangentes aux points B et C à la représentation
graphique de la fonction f soient parallèles à l’axe des abscisses.
Déterminer la valeur du réel c.
f '(0) =0= b p/4cos (c).
B n'est pas nul, donc c = p / 2.
2. Déterminer les réels a et b.
f (x) = a + b sin (0,5p+px/4).
f(0) = 1 = a + b sin (0,5p)= a+b.
f(4) = 3 = a + b sin (0,5p+p) = a-b.
Par suite a = 2 et b = -1.
Partie B - Approximation du volume de l’ampoule
Par rotation de la figure précédente autour de l’axe des abscisses, on obtient un modèle de l’ampoule.
Afin d’en calculer le volume, on la décompose en trois parties comme illustré ci-dessous :
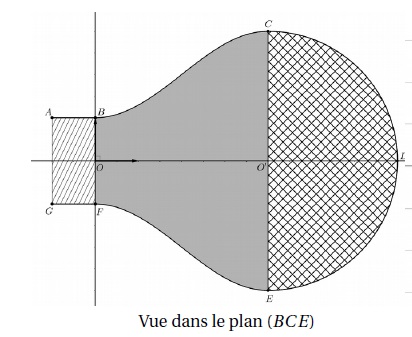
On admet également que, pour tout réel x de l’intervalle [0 ; 4], f (x)= 2-cos(px/4).
1. Calculer le volume du cylindre de section le rectangle ABFG.
Hauteur AB = 1 ; aire de base pR2 = p *12 = p.
Volume du cylindre p.
2. Calculer le volume de la demi-sphère de section le demi-disque de diamètre [CE].
Volume d'une sphère 4 / 3 p r3 avec r = 3.
4 / 3 p *27 = 36 p.
Volume de cette demi sphère : 18 p.
3. Pour approcher
le volume du solide de section la zone grisée BCEF, on partage le
segment [OO'] en n segments de même longueur 4 / n puis on construit n
cylindres de même hauteur 4 / n.
a) Cas particulier : dans cette question uniquement on choisit n = 5.
Calculer le volume du troisième cylindre, grisé dans les figures ci-dessous, puis en donner la valeur arrondie à 10-2.
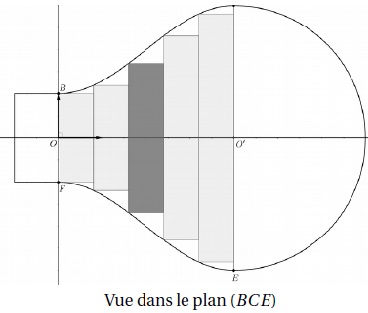
Hauteur de ce cylindre : 4 / 5.
Rayon de ce cylindre f(8 /5) = 2-cos(2p/5).
Volume de ce cylindre : 4 p / 5(2-cos(2p/5))2 ~7,19 unité de volume.
b) Cas général : dans cette question, n désigne un entier naturel quelconque non nul.
On approche le volume du solide de section BCEF par la somme des
volumes des n cylindres ainsi créés en choisissant une valeur de n
suffisamment grande.
Recopier et compléter l’algorithme suivant de sorte qu’à la fin de son
exécution, la variable V contienne la somme des volumes des n cylindres
créés lorsque l’on saisit n.
Volume d'un cylindre : V = 4 p / n (2-cos(pk/n))2
V <-- 0
Lire n
Pour k allant de 1 à n :
V <--V+4 p / n (2-cos(pk/n))2
Fin Pour
|
|
Exercice
4.
Un
lapin se déplace dans un terrier composé de trois galeries, notées A, B
et C, dans chacune desquelles il est confronté à un stimulus
particulier.
A chaque fois qu’il est soumis à un stimulus, le lapin reste dans la
galerie où il se trouve ou change de galerie. Cela constitue une
étape.
Soit n un entier naturel.
On note an la probabilité de l’événement : « le lapin est dans la galerie A à l’étape n ».
On note bn la probabilité de l’événement : « le lapin est dans la galerie B à l’étape n ».
On note cn la probabilité de l’événement : « le lapin est dans la galerie C à l’étape n ».
À l’étape n = 0, le lapin est dans la galerie A.
Une étude antérieure des réactions du lapin face aux différents stimuli
permet de modéliser ses déplacements par le système suivant :
an+1 = an / 3 +bn / 4.
bn+1 = 2an / 3 +bn / 2 + 2cn / 3.
cn+1 = cn / 3 +bn / 4.
L’objectif de cet exercice est d’estimer dans quelle galerie le lapin a la plus grande probabilité de se trouver à long terme.
Partie A.
À l’aide d’un tableur, on obtient le tableau de valeurs suivant :
|
A
|
B
|
C
|
D
|
1
|
n
|
an
|
bn
|
cn
|
2
|
0
|
1
|
0
|
0
|
3
|
1
|
0,333
|
0,667
|
0
|
4
|
2
|
0,278
|
0,556
|
0,167
|
5
|
3
|
0,231
|
0,574
|
0,194
|
6
|
4
|
0,221
|
0,571
|
0,208
|
7
|
5
|
0,216
|
0,572
|
0,212
|
8
|
6
|
0,215
|
0,571
|
0,214
|
9
|
7
|
0,215
|
0,571
|
0,214
|
10
|
8
|
0,214
|
0,571
|
0,214
|
11
|
9
|
0,214
|
0,571
|
0,214
|
12
|
10
|
0,214
|
0,571
|
0,214
|
1. Quelle formule faut-il entrer dans la cellule C3 et recopier vers le bas pour remplir la colonne C?
=2*B2/3+C2/2+2*D2/3
2. Quelle conjecture peut-on émettre ?
La suite (an) converge vers 0,214 ; la suite (bn) converge vers 0,571 ; la suite (cn) converge vers 0,214.
|
|
Partie B.
1. On définit la suite (un), pour tout entier naturel n, par un = an -cn.
a) Démontrer que la suite (un) est géométrique en précisant sa raison.
un+1 = an / 3 +bn / 4-cn / 3 -bn / 4.
un+1 = an / 3 -cn / 3.
un+1 = un / 3.
Il s'agit d'une suite géométrique de raison 1 / 3 et de premier terme u0 = 1
b) Donner, pour tout entier naturel n, l’expression de un en fonction de n.
un = 1 / 3n.
2. On définit la suite (vn) par vn = bn -4/7 pour tout entier naturel n.
a) Expliquer pourquoi pour tout entier naturel n, an +bn +cn = 1 et en déduire que pour tout entier naturel n, vn+1 = -vn / 6.
Les trois évènements A, B, C forment une partition de l'univers et la somme de leurs probabilités est égale à 1.
vn = bn -4/7 = 1-an-cn-4 / 7=3 / 7-an-cn.
vn+1 = 3 / 7-an+1-cn+1.
vn+1 = 3 / 7-an/ 3 -bn/4- cn / 3 -bn / 4.
vn+1 = 3 / 7-an/ 3 -bn/2- cn / 3.
an + cn =1-bn ;
vn+1 = 3 / 7- bn/2- (1-bn) / 3.
vn+1 = 3 / 7-1/3- bn/6.
vn+1 = 2 / 21- bn/6.
vn+1 = (4 / 7- bn ) /6 = -vn / 6.
b) En déduire, pour tout entier naturel n, l’expression de vn en fonction de n.
Il s'agit d'une suite géométrique de raison -1 / 6 et de premier terme v0 = -4/7
vn = -4 / 7 *1/ (-6)n.
3. En déduire que pour tout entier naturel n, on a :
an = 3/14+0,5(1/3)n +2/7(1/(-6)n; bn = 4/7-4/7(-1/6)n ; cn = 3 /14-0,5(1/3)n +2/7(-1/6)n.
bn = vn +4/7 = -4 / 7 *1/ (-6)n+ 4/7.
an = un +cn =un +1-bn-an .
2an =un +1-bn =1 / 3n+1-4/7 +4 / 7 *1/ (-6)n.
2an =3/7+1/3n+4 / 7 *1/ (-6)n.
an = 3/14+0,5(1/3)n +2/7(1/(-6)n;
cn = 1-bn-an.
cn = 1+ 4 / 7 *1/ (-6)n- 4/7 -3/14-0,5(1/3)n- 2/7(1/(-6)n ;
cn =3 / 14 +2 / 7 *1/ (-6)n -0,5(1/3)n.
4. Que peut-on en déduire sur la position du lapin après un très grand nombre d’étapes ?
0 < 1 / 3 < 1 ; (1/3)n tend vers zéro quand n tend vers plus l'infini.
an tend vers 3 /14 ~0,214 quand n tend vers plus l'infini.
-1 < -1/6 < 1; (-1/6)n tend vers zéro quand n tend vers plus l'infini.
bn tend vers 4 / 7 ~0,571quand n tend vers plus l'infini.
cn tend vers 1-3/14-4/7 = 3/14 ~0,214.
Après un grand nombre d'étapes, la probabilité que le lapin soit dans
la galerie A est 3/14 ; la probabilité qu'il soit en B est de 4 / 7 ;
la probabilité qu'il soit en c est 3 /14.
|
|