Mathématiques,
fonction, probabilités,
Bac S Antilles 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
L’exploitant
d’une forêt communale décide d’abattre des arbres afin de les vendre,
soit aux habitants, soit à des entreprises. On admet que :
• parmi les arbres abattus, 30 % sont des chênes, 50 % sont des sapins
et les autres sont des arbres d’essence secondaire (ce qui signifie
qu’ils sont de moindre valeur) ;
• 45,9 % des chênes et 80 % des sapins abattus sont vendus aux habitants de la commune;
• les trois quarts des arbres d’essence secondaire abattus sont vendus à des entreprises.
Partie A.
Parmi les arbres abattus, on en choisit un au hasard.
On considère les événements suivants :
• C : « l’arbre abattu est un chêne » ;
• S : « l’arbre abattu est un sapin » ;
• E : « l’arbre abattu est un arbre d’essence secondaire » ;
• H : « l’arbre abattu est vendu à un habitant de la commune ».
1. Construire un arbre pondéré complet traduisant la situation.
2. Calculer la probabilité que l’arbre abattu soit un chêne vendu à un habitant de la commune.
3. Justifier que la probabilité que l’arbre abattu soit vendu à un habitant de la commune est égale à 0,587 7.
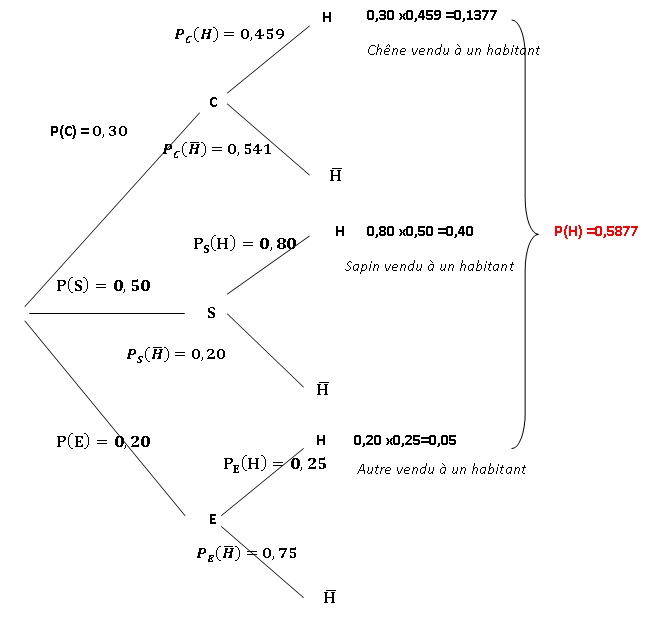
4. Quelle est la probabilité qu’un arbre abattu vendu à un habitant de la commune soit un sapin ?
On donnera le résultat arrondi à 10−3.
0,40 / 0,5877 ~ 0,681.
.
|
|
Partie B.
Le nombre d’arbres sur un hectare de cette forêt peut être modélisé par
une variable aléatoire X suivant une loi normale d’espérance μ= 4000 et
d’écart-type σ = 300.
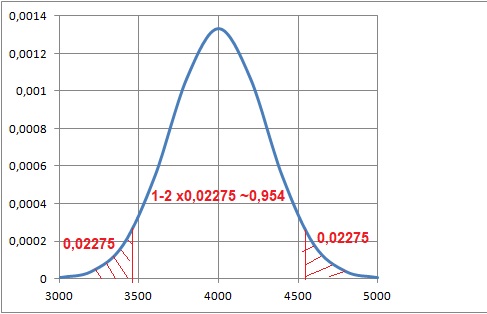
1. Déterminer la
probabilité qu’il y ait entre 3 400 et 4 600 arbres sur un hectaure
donné de cette forêt. On donnera le résultat arrondi à 10−3.
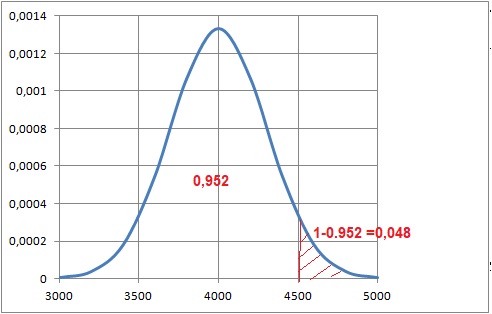
2. Calculer la
probabilité qu’il y ait plus de 4 500 arbres sur un hectare donné de
cette forêt. On donnera le résultat arrondi à 10−3.
Partie C.
L’exploitant affirme que la densité de sapins dans cette forêt communale est de 1 sapin pour 2 arbres.
Sur une parcelle, on a compté 106 sapins dans un échantillon de 200
arbres. Ce résultat remet-il en cause l’affirmation de l’exploitant ?
On assimile le comptage des sapins à un tirage avec remise. taille de l'échantillon n = 200 ;
Proportion supposée de sapins p = 0,5.
n > 30 ; np = 100 > 5 ; n(1-p) = 100 > 5.
Les conditions sont réunies pour définir un intervalle de fluctuation au seuil de 95 %.
1,96 [(p(1-p) / n]½ = 1,96 x[0,5 x0,5 / 200]½ = 0,069.
I = [0,5-0,069 ; 0,5 +0,069] soit [0,431 ; 0,569].
La fréquence observée 106 / 200 = 0,53 appartient à cet intervalle. L'affirmation n'est pas remise en cause.
|
|
Exercice 3.
Un publicitaire souhaite imprimer le logo ci-dessous sur un T-shirt :
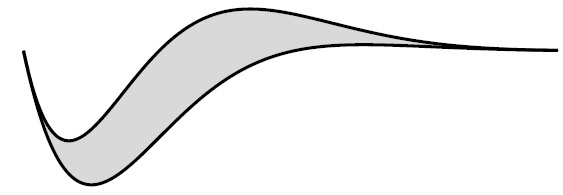 Il dessine ce logo à l’aide des courbes de deux fonctions f et g définies sur R par :
f (x) = e−x (−cosx +sinx +1) et g (x)= −e−x cosx.
On admet que les fonctions f et g sont dérivables sur R.
Partie A. Étude de la fonction f.
1. Justifier que, pour tout x appartenant à R :
−e−x < f (x) < 3e−x .
Il dessine ce logo à l’aide des courbes de deux fonctions f et g définies sur R par :
f (x) = e−x (−cosx +sinx +1) et g (x)= −e−x cosx.
On admet que les fonctions f et g sont dérivables sur R.
Partie A. Étude de la fonction f.
1. Justifier que, pour tout x appartenant à R :
−e−x < f (x) < 3e−x .
-1 < cos x < 1 et -1 < sin x < 1.
-1-1+1 < -cos x + sin x+1 <1 +1 +1.
En multipliantmembre à membre par e-x >0 : −e−x < f (x) < 3e−x .
2. En déduire la limite de f en +oo.
Quand x tend vers plus l'infini : −e−x et 3e−x tendent vers zéro.
Le théorème des gendarmes conduit à : f(x) tend vers zéro quand x tend vers plus l'infini.
3. Démontrer que, pour tout x réel, f ′(x) = e−x (2cos x −1) où f ′ est la fonction dérivée de f .
On pose : u = e-x et v = -cos x + sin x +1 ; u' = -e-x ; v' = sin x + cos x.
u'v + v'u = -e-x (sin x + -cos x +1)+ e-x (sin x + cos x).
f ' (x) = e−x (2cos x −1)
4. Dans cette question, on étudie la fonction f sur l’intervalle [−p ; p].
a. Déterminer le signe de f ′(x) pour x appartenant à l’intervalle [−p ; p].
e−x est strictement positif ; 2 cos x -1 s'annule pour x = ± p/3.
2 cos x -1 est négatif sur [−p ; -p/3] et sur [p/3 ; p]
2 cos x -1 est positif sur [−p/3 ; p/3].
b. En déduire les variations de f sur [−p ; p].
Sur [−p ; -p/3] et sur [p/3 ; p], f(x) est strictement décroissante.
Sur [−p/3 ; p/3] f(x) est strictement croissante.
f(x) présente un minimum en -p/3 et un maximum en p/3.
Partie B. Aire du logo.
On note Cf et Cg les représentations graphiques des fonctions f et g dans un repère orthonormé
L’unité graphique est de 2 centimètres. Ces deux courbes sont tracées.
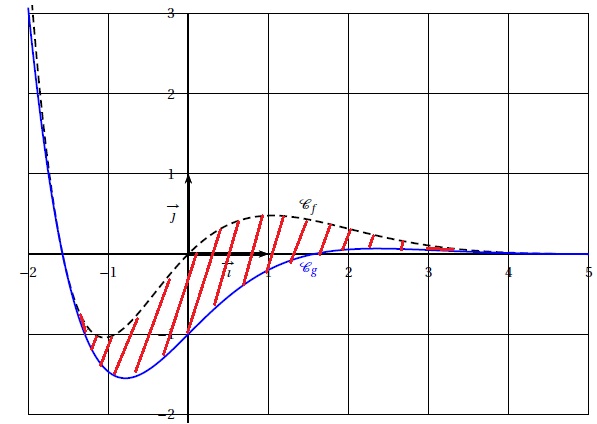
1. Étudier la position relative dela courbe Cf par rapport à la courbre Cg sur R.
f (x) -g(x) = e−x (−cosx +sinx +1) +e−x cosx = e−x ( sinx +1).
-1 < sin x < 1 ; -1 +1 < sin x + 1 < 1 +1 ; 0 < sin x + 1 < 2 ;
de plus e-x est strictement positif.
f (x) -g(x) > 0, donc Cf est au dessus de Cg.
2. Soit H la fonction définie sur R par :
H(x) = -0,5 ( cos x+ sin x+2)e-x.
On admet que H est une primitive de la fonction (sinx +1)e−x sur R.
On note D le domaine délimité par la courbe Cf , la courbe Cg est les droites d’équation x = -0,5p et 1,5 p.
a. Hachurer le domaine D sur le graphique.
b. Calculer, en unité d’aire, l’aire du domaine D, puis en donner une valeur approchée à 10−2 près en cm2.
Aire du domaine D : A =H(1,5 p) - H(-0,5p) = -0,5 [ cos (1,5 p)+ sin (1,5 p)+2]e-(1,5 p)+0,5[ cos (-0,5 p)+ sin (-0,5 p)+2]e0,5 p.
A = -0,5(0-1+2)e-(1,5 p)+0,5(0-1+2)e0,5 p.
A = -0,5e-(1,5 p)+0,5e0,5 p ~ -0,0045 +2,41 ~2,40 unités d'aire soit 2,40 x4 =9,60 cm2.
|
|