Mathématiques,
fonction, probabilités,
Bac S Métropole 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
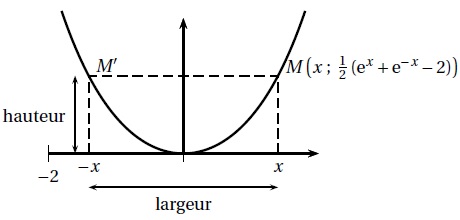
On a représenté ci-dessous la courbe d'équation y = 0,5 (ex+e-x-2).
On définit la "largeur" et la "hauteur" de l'arc de chaînette
délimité par les points M et M".
Le
but de cet exercice est d'étudier les positions possibles sur la courbe
du point M' d'abscisse x strictement positive afin que la largeur de
l'arc soit égale à sa hauteur.
1. Justifier que ce problème se
ramène à la recherche des solutions strictement positives de l'équation
(E) : ex+e-x-4x-2=0.
La hauteur est égale à y =0,5 (ex+e-x-2)
et la largeur est égale à 2x.
0,5 (ex+e-x-2)
= 2x soit ex+e-x-4x-2=0.
2. On note f la fonction définie sur
[0 ; +oo[ par f(x) = ex+e-x-4x-2.
2.a. Vérifier que
pour tout x >0, f(x) = x(ex / x-4) +e-x-2.
f(x) = x ex
/ x - 4x +e-x-2 = ex-4x+e-x-2
2.b. Déterminer la limite de f(x)
quand x tend vers l'infini.
Quand x tend vers plus l'infini :
e-x tend vers zéro.
x(ex
/ x-4) tend vers plus l'infini.
Par somme de limite f(x) tend vers plus l'infini.
3.a. Calculer f '(x), fonction
dérivée de f(x).
f '(x) = ex-e-x-4.
3.b. Montrer que f
'(x) =0 équivaut à : (ex)2-4ex-1=0.
ex(ex-e-x-4)
=0 ; (ex)2 -1 -4ex=0.
3.c. On pose X = ex.
Montrer que f '((x) = 0 admet une unique solution réelle ln(2+5½).
X2 -4X-1 = 0 ; déterminant D = 16+4 = 20.
On ne retient que la solution positive car ex >0 : X =
(4+20½) / 2 = 2 +5½ ; x = ln X = ln(2+5½).
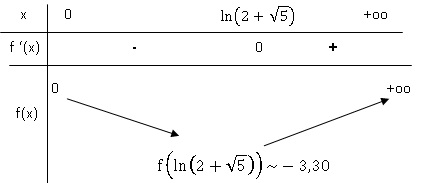
4. On donne le tableau de signes de
la fonction f '(x).

4.a. Dresser le
tableau de variation de la fonction f.
4.b. Démontrer que
l'équation f(x) = 0 admet une unique solution strictement positive
notée a.
Sur [0 ; ln(2+ 5½)], f(x) est négative donc f(x) = 0 n'a pas
de solution.
Sur [ ln(2+
5½) ; +oo[, f(x) est continue est strictement croissante ;
de plus la valeur zéro appartient à [f( ln(2+ 5½))
; +oo[ donc
d'après le corollaire du théorème des valeurs intermédiaires,
l'équation admet une solution unique.
5. On considère l'algorithme suivant
où les variables a, b et m sont réelles.
Tant que b-a >0,1 faire :
m <-- (a+b) / 2
Si em +e-m-4m-2 >0, alors
b <--m
Sinon : a <-- m
Fin Si
Fin tant que.
a. Les valeurs
initiales de a et b sont respectivement 2 et 3. Que contiennent-elles à
la fin de l'exécution de l'algotithme ? Justifier en complétant le
tableau suivant.
m
|
a
|
b
|
b-a
|
f(m)
|
|
2
|
3
|
1
|
|
2,5
|
2
|
2,5
|
0,5 > 0,1
|
~ 0,264 > 0
|
2,25
|
2
|
2,5
|
0,5 > 0,1
|
~ -1,4 < 0
|
2,375
|
2,25
|
2,5
|
0,75 > 0,1
|
~ -0,66 < 0
|
2,4375
|
2,375
|
2,5
|
0,125
> 1
|
~
-0,218 < 0
|
2,46875
|
2,4375
|
2,5
|
0,0625
< 0,1
|
|
On obtient
un encadrement de a
: 2,4375 < a
< 2,5.
6. La Gateway Arch
a l'allure ci-contre 
Son profil peut être approché par un arc de chaînette renversé dont la
largeur est égale à la hauteur.
La largeur de cet arc ( exprimée en mètre ) est égale au double
de la solution strictement positive de l'équation :
(E') :et/39 +e-t / 39 -4t /39 -2 = 0.
Donner un encadrement de la hauteur de la Gateway Arch.
t = 39a ; 2t = 78 a.
78 x2,4375 < hauteur < 2,5 x78 ; 190 < hauteur < 195.
|
|
Exercice 2. Partie A.
Une étude est menée dans la population d'une ville à l'issue de la
période hivernale :
40 % de la population a été vaccinée contre la grippe.
8 % des personnes vaccinées ont contracté la grippe.
20 % de la population a contracté la grippe.
On choisit au hasard une personne dans la population de la ville et on
considère les évènements :
V : "personne vaccinée contre la grippe".
G " la personne a contracté la grippe".
1.a Donner la probabilité de
l'évènement G.
P(G) = 0,20.
1.b.Compléter
l'arbre pondéré ci-dessous :
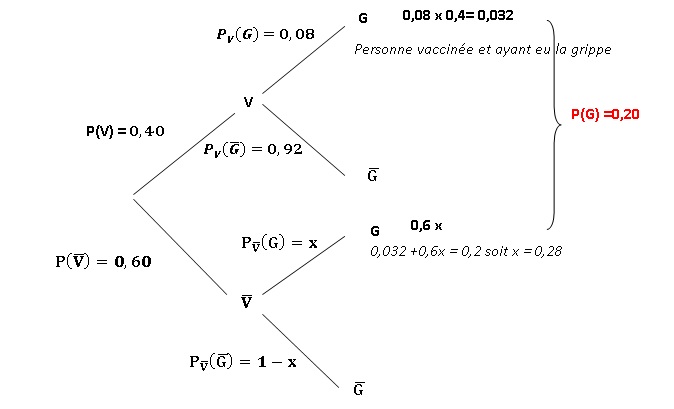
2. Déterminer la
probabilité que la personne choisie ait contracté la grippe et soit
vaccinée. 0,032.
3. La personne
choisie n'est pas vaccinée. Montrer que la probabilité qu'elle ait
contracté la grippe est égale à 0,28.
Partie B.
On note X la variable aléatoire égale au nombre de personnes vaccinées
parmi les n interrogées.
1. Quelle est la loi de probabilité
suivie par X ?
Les
n expériences sont identiques, indépendantes et aléatoires. deux issues
sont possibles ( être vacciné avec une probabilité de 0,4 ou ne pas
être vacciné ). X suit une loi binomiale B( n ; 0,4).
2 Dans cette question, on suppose n
= 40.
a. Déterminer la
probabilité qu'exactement 15 des 40 personnes interrogées soient
vaccinées.
Loi B (40 ; 0,4) ; B(X = 15 ) = 0,123.
b. Déterminer la
probabilité qu'au moins la moitié des personnes interrogées soient
vaccinées.
Loi B (40 ;
0,4) ; B(X > 20 )
=1-P(X <20) = 1 -P(X <
19) = 1-0,870 =0,130.
3. On interroge un
échantillon de 3750 habitants de la ville. On note Z la variable
aléatoire définie par Z = (X -1500) / 30.
La loi de probabilité de
Z peut être approchée par la loi normale centrée réduite.
Déterminer la probabilité qu'il y ait entre 1450 et 1550 habitants
vaccinés dans cet échantillon.
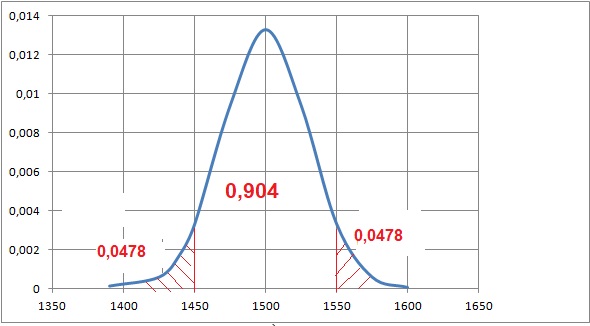
P(1450 < X < 1550) = 0,904.
|
|
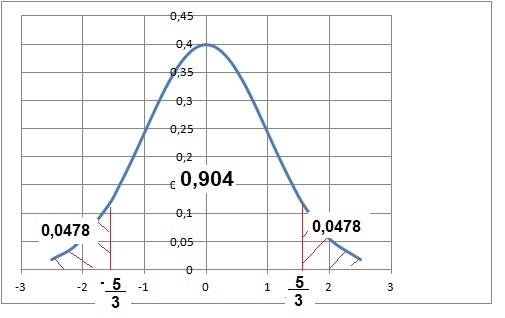 . .
P(-5 / 3 < Z < 5 / 3) = 0,904.
|
|