Mathématiques,
Suites numériques
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
2017.
10) On
considère la suite (un) définie par u0 = 5 et un+1=un+4
pour tout entier naturel, alors u23=
A : 119
B : 85
C : 97
D : 111
Suite arithmétique de
premier terme 5 et de raison 4 : u23
= 5 +23 x4 = 97.
11) On considère
la suite (un) définie par un =(-1)n x
E(n/3) / (n2+n+1) , où E(x) désigne la partie entière de x,
alors
A : (un) n’est ni minorée, ni majorée.
B : (un) est minorée mais pas majorée.
C : (un) est majorée mais pas minorée.
D : est bornée.
La présence de (-1)n élimine les propositions B et C.
Quand n devient grand, (un)
, u2n tend vers zéro par valeur positive et u2n+1
tend vers zéro par valeur négative.
12. On considère une suite (un)
arithmétique de raison 3 et une suite (vn) arithmétique de
raison 2, alors la suite (wn) définie par wn=un+vn
vn est
A : arithmétique de raison 6.
B : géométrique de raison 5.
C : arithmétique de raison .
D : arithmétique de raison
5.
un+1
=3+ un ; vn =2 + vn ; wn
=5 + vn +un.
13) On considère
une suite géométrique (un) de raison 3 et une suite
géométrique (vn) de raison 2, alors la suite alors
la suite (wn) définie par wn=un x vn vn
est
A : géométrique de raison 6.
B : géométrique de raison 5.
C : géométrique de raison 9.
D : géométrique de raison 8.
un+1 =3 un ; vn+1 =2 vn ; wn
=6 vn un
14)
On considère une suite (un) géométrique de raison 3 et une
suite (vn) géométrique de raison 2, alors la suite (wn)
définie par wn = 0,5(un+vn) est
A : géométrique de raison 2,5.
B : arithmétique de raison2,5 .
C : arithmétique de raison 4,5.
D : ni arithmétique, ni
géométrique.
un+1 =3 un ; vn+1 =2 vn ; wn
=0,5(3un + 2vn).
.
|
|
2016.
1. On considère la
suite géométrique (un) de raison q=0,5 et u4=32.
Alors pour tout n entier :
a. un =
32 +(n-4) / 2.
u4 = u0 x (0,5)4 =32 ; un
= u0 x (0,5)n =u0 x (0,5)4
x0,5n-4 =32 x (0,5)n-4.
b. un = 32 x (0,5)n.
c. un =
32 x (0,5)n-4. Vrai.
d.
un = 32 + (0,5)n-4.
2. On considère les deux suites (un)
et (uv) définies par u0=5 ; un+1 =
0,25(3un+vn) et v0=5
; vn+1 = (un+5vn)/6 . On admet que (un)
converge vers l1 relet que (vn) converge vers l2
réel , alors :
a. l1=l2.
Vrai.
b. l1<l2.
c. l1>l2.
d. On ne dispose pas assez
d'informations pour comparer l1 et l2.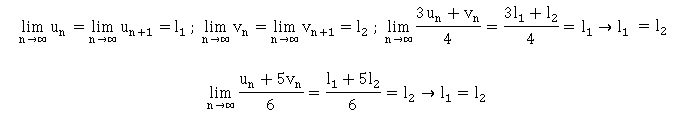
3. On considère une
suite (un) strictement croissante de premier terme u0
=2 et la suite (vn) définie pour tout n entier pa
vn = -2 /(1-3un) . Alors la suite est (vn)
:
a : monotone et
croissante.
b : monotone et
décroissante. Vrai.
c : non monotone
d : Aucune des 3
réponses précédentes n’est exacte.
vn
=-2 /(1-3un) ; vn+1
=-2 /(1-3un+1) ; un+1 >un
entraîne 1-3un+1 <1-3un entraîne 1/(1-3un+1 ) > 1 (1-3un )
entraîne : -2/(1-3un+1 ) < -2 (1-3un )
On
considère la suite (un) définie par u0=7 et un+1=f(un)
pour tout n entier, où est la fonction définie sur [4 : +oo[
représentée ci-dessous :
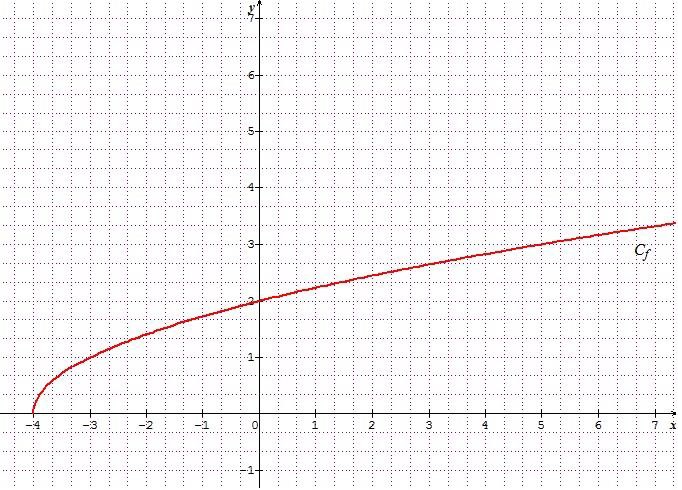
4. La suite (un) est :
a : monotone et
croissante.
b : monotone et
décroissante. Vrai.
c : non monotone.
d : Aucune des 3
réponses précédentes n’est exacte.
u1 = f(u0) = f(7) ~3,33 ; u2 = f(u1)
~2,7 ; u3 = f(u2)
~2,65 ;
u4 = f(u3) ~2,55.
5.
La suite (un):
a : converge vers 2.
b : diverge vers
+oo.
c : converge vers
-4.
d : converge vers l
appartenant à [2 ; +oo[. Vrai. |
|
2015.
Soient (A n) et (B n) les suites définies pour n supérieur ou égal à 1 par : 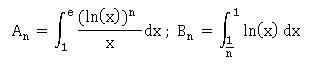 50
50. (B n) est :
a. constante ; b. strictement décroissante. Vrai c. strictement croissante. d.non monotone.
Primitive de ln(x) :F= x (ln(x)-1) ; F(1) = -1 ; F(1/n) = -1/n (ln(n)+1) ; B n = -1+1/n (ln(n)+1).
51 Pour tout n supérieur ou égal à 2, (B n) est :
a. strictement négatif Vrai ; b. strictement pôsitif ; c. nul ; d. Aucune des 3 réponses précédentes
n'est exacte.
52. A 1=
a. 1/4 ; b. 1/3 ; c. 1/2, Vrai ; d. 1.
Primitive de ln(x) / x ; on pose u = ln(x) ; u' = 1/x ; primitive de u u' = ½u 2 soit 0,5 (ln(x)) 2.
A 1 = 0,5 (ln(e)) 2-(ln(1)) 2=0,5 x1-0=0,5.
53. A 2=
a.1/4 ; b. 1/3 Vrai
; c. 1/2 ; d. 1.
On pose U = ln(x) ; U' = 1/x ; (ln(x) 2 / x =U 2U' ; primitive de U 2U' =U 3 / 3 =( ln(x)) 3 / 3.
A 2 =( ln(e)) 3 / 3 -( ln(1)) 3 / 3 = 1/3-0=1/3.
54. (A n) est :
a. constante ; b. strictement décroissante Vrai
; c. strictement croissante ; d. non monotone.
55. (A n)
a. converge Vrai ; b. diverge vers -oo ; c. diverge vers +oo ; d. diverge sans limite.
|
|