Mathématiques,
suites numériques, concours Audioprothésiste Bordeaux
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
2018.
Exercice5.
On considère la suite (un) définie par u0 = 1 et pour tout entier n un+1 = 2un / (2+3un) et la suite (vn) par vn = 1 +2 / un.
Question
14
La suite (un) :
A. est arithmétique de raison -2 / 5. Faux.
u1 = 2 / 5 ; u2 = 1/4 ; u3 = 2/11.
B. est arithmétique de raison 3. Faux.
C. est géométrique de raison 2 / 5. Faux.
D. est géométrique de raison 3. Faux..
E. n'est ni arithmétique, ni géométrique. Vrai.
Question
15.
La suite (vn) :
A. est arithmétique de raison -2 / 5. Faux.
v0 = 3 ; v1 = 6 ; v2 = 9.
vn+1 = 1 +(2+3un) / un = 4+2/un = 3 +vn.
B. est arithmétique de raison 3.Vrai.
C. est géométrique de raison 2 / 5. Faux.
D. est géométrique de raison 3. Faux..
E. n'est ni arithmétique, ni géométrique. Faux .
Question
16
Le terme général de la suite (un) s'exprime pour tout entier n : :
A. 2 / (2n+3). Vrai.
B. 2 / (2-3n).
Faux.
C. 2 / (3n-2). Faux.
D. 2 / 3+2n.
Faux.
E. aucune des propositions ci-dessus.
Faux.
.
|
|
Complexes et géométrie.
12. L'écriture
exponentielle de 2-2i est :
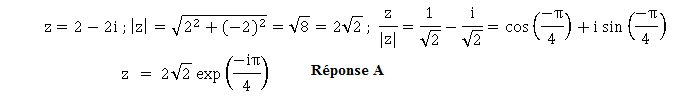
Dans les 4 items suivants on considère
les nombres complexes z1 = 2 exp(ip/9) et z2 = -2 exp(-ip/9)
13. z127
est
A. un réel strictement positif
;
B. un réel strictement
négatif ; vrai ;
C. un
imaginaire pur
;
D. nul ;
E. aucune des propositions
précédentes.
227 exp((ip/9 x27) = 227 exp((3ip)
=227 exp((ip)
= -227 .
14. z118 est
A. un réel strictement positif
;
vrai ;
B. un réel strictement négatif ;
C. un
imaginaire pur
de partie imaginaire strictement positive;
D. un
imaginaire pur
de partie imaginaire strictement négative;
E. aucune des propositions
précédentes.
218 exp((ip/9 x18) = 218 exp((2ip)
= 218.
.
15. On a :
A. z1 = z2; B.
z1 = - z2;
C.
z1 = conjugué de z2;
D. z1 = -conjugué de z2;
E. aucune des propositions
précédentes. Vrai.
z1 = 2( cos ( p/9)
+i sin (p/9)
; z2
= -2( cos ( -p/9)
+i sin (-p/9)
=
2( -cos ( p/9) +i
sin (p/9).
15. On a :
A. z1 = z2; B.
z1 = - z2;
C.
z1 =
conjugué de z2;
D. z1 = -conjugué de z2;
E. aucune des propositions
précédentes. Vrai.
16. z1 +z2
est un :
A. reél strictement positi f; B.
un réel strictement
négatif ;
C.
un imaginaire pur
de partie imaginaire strictement positive ; vrai
D. un imaginaire pur de
partie imaginaire strictement négative ;
E. aucune des propositions
précédentes. Vrai.
2( cos ( p/9) +i sin (p/9)+2( -cos ( p/9) +i sin (p/9)
=4isin
(p/9)~2,47
i.
17. L'écriture
algébrique du nombre complexe z est :
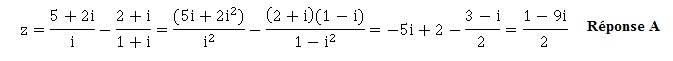
|
|
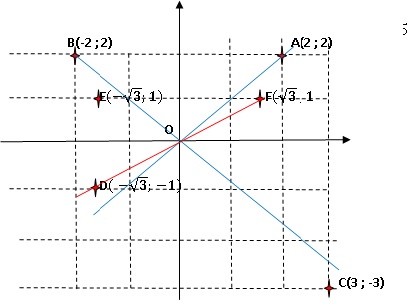
On
se place dans le plan complexe d'origine O.
Affixe de A : zA = 2+2i ; affixe de B : zB =-2+2i ,
affixe de C : zC = a-3i avec a un réel ;
affixe de D : zD = -3½-i ; affixe de E : zE = -3½+i
; affixe
de F : zF = 3½+i.
18. Le triangle AOC est rectangle en
O si a est égal à :
:
A. 2 ; B. 3 vrai ; C. -2 ; D.
-3; E. aucune
des propositions précédentes.
OA2 =22+22 = 8 ; OC2
=a2+(-3)2 = 9+a2 ; AC2 =
(a-2)2 +(-3-2)2=a2-4a+29.
OA2
+OC2
=AC2
; 17+a2
=a2-4a+29
; 4a=12 ; a=3.
On prend pour la suite la valeur de a
telle que le triangle OAC est rectangle en O.
19.
On
a :
A.
Le triangle AOB est rectangle en A
; B. Le
triangle AOB est rectangle en O vrai
; C.
Le triangle DOE est rectangle en D ;
D. Le triangle AOB
est équilatéral ; E. aucune
des propositions précédentes.
20.
On
a :
A.
Le triangle AOF est rectangle ; B. Le
triangle DOE est rectangle en O ;
C.
Le triangle AOF est isocèle ;
D. Le triangle DOE
est équilatéral ; E. aucune
des propositions précédentes. Vrai.
21.
On
a :
A.
Le triangle AOC est équilatéral ; B. Le
triangle DOB est rectangle ; C.
Le triangle AOB est isocèle vrai ;
D. Le triangle AOB
est équilatéral ; E. aucune
des propositions précédentes.
OA2 =22+22 = 8 ; OB2
=(-2)2+22 = 8 ; AB2 = (-4)2
+(0)2=16.
22. On a :
A.
Les points A, O et D sont alignés
; B. Les
points B, O et C sont alignés ;
C.
Les points E, O et B sont alignés ;
D. Les
points A, O et F sont alignés ; E. aucune
des propositions précédentes. Vrai.
23.
On
a :
A.
Les points A, O et E sont alignés
; B. Les
points F, O et D sont alignés vra i;
C.
Les points E, O et F sont alignés ;
D.Les
points B, O et D sont alignés ; E. aucune
des propositions précédentes.
Exercice 3.
On considère le nombre complexe z = 5 i exp(ip/8) :
10. Le module de z
est :
A. 1 ; B. 5, vrai. C. -5 ; D. 25. E. 5½.
11. L'argument de z
est :
A. -p/8. B. p/8.
C.
5p/8,
vrai.
D.
3p/8 ; E. -5p/8.
z = 5 exp(ip/2) exp(ip/8) =5 exp(i(p/2+p/8)).
12. z2 est :
A. un réel strictement positif
;
B. un réel strictement
négatif ;
C. un
imaginaire pur
de partie imaginaire strictement positive
;
D. un
imaginaire pur
de partie imaginaire strictement négative ;
E. aucune des propositions
précédentes vrai.
z2 = 25 exp(5ip/4) =25 ( cos(5p/4)+
i sin(5p/4)) .
13. arg(z2)
est
A. 5p/4, vrai
; B. p/4 ;
C. 0
; D. p/ 2 ; E.2
5p/
64.
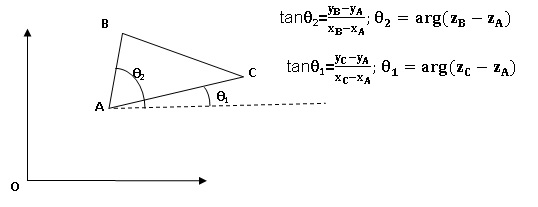
Exercice 4.
On considère un triangle ABC quelconque non aplati. Les points A, B et
C ont pour affixes respectives zA, zB et zC.
14. L'angle CAB est obtenu en
calculant :
A. arg(zB)-arg(zC) ;
B. arg(zB)
/arg(zC
);
C. [ arg(zB
-zA)]
/ [arg(zC-zA)];
D. [ arg(zB)-arg(zA)]
/ [arg(zC)-arg(zA)];
E. arg(zB
-zA)
- arg(zC-zA). Vrai.
Exercice 5.
Soient
A et b deux points non confondus et I le milieu du segment [AB]. Dans
le plan complexe, les points A, B et I, ont pour affixes respectifs zA,
zB, zI.
15.
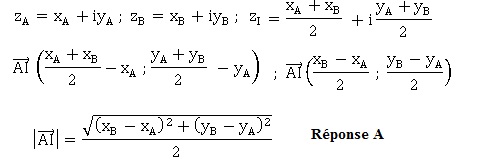
Exercice 6.
16. L'affixe de B est alors :
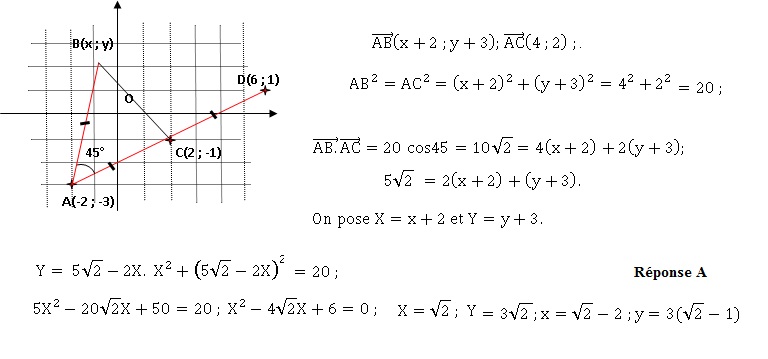
17. L'affixe de D
est :
A.
2-i ; B. 6+i vrai ; C. -2i ; D.
4; E. aucune
des propositions précédentes.
C milieu de [AD] ; xC = 0,5(xA +xD) ; xD=2xC -xA =4-(-2)=6.
yC = 0,5(yA
+yD) ;yD=2yC -yA =-2-(-3)=1.
|
|