Mathématiques,
Nombres complexes, concours Audioprothésiste Bordeaux
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
On se place dans le plan complexe orienté.
Question 10.
L'ensemble des points M d'affixe z vérifiant |z-i+1| =|z-1| est :
A. une droite. Vrai.
B.un cercle
c. une parabole
D. une hyperbole
E. un carré.
z = x+iy ; z-i+1 = x+1+i(y-1) ; |z-i+1| =( (x+1)2+(y-1)2 )½.
z-1 = x-1 +iy ; |z-1| =( (x-1)2+y2 )½.
(x+1)2+(y-1)2 = (x-1)2+y2 ; 4x-2y+1=0 ; y =2x+0,5.
d.
Pour tout entier naturel n, le triangle OAn An+1
est isocèle et rectangle. Faux.
Question 11
Les points M d'affixe z solutions de l'équation z4 = 16 sont :
A. tous alignés
B. sur un cercle de centre O et de rayon 16.
C. les sommets d'un carré dont la longueur de la diagonale vaut 2.
D. les sommets d'un carré dont la longueur de la diagonale vaut 4. Vrai.
E. les sommets d'un carré dont la longueur de la diagonale vaut 32.
On pose Z = z2 ; Z1 = 4 et Z2 = -4.
z1 = 2 ; z2 = -2 ; z3 = 2i ; z4 = -2i.
Dans le plan complexe orienté on considère l'équation (E) : z 4 +z 3 +5z 2+z+4=0.
Question 12
L'équation (E) admet exactement :
A. aucune racine imaginaire pure
B. une racine imaginaire pure.
C. deux racines imaginaires pures. Vrai.
D. trois racines imaginaires pures.
E. quatre racines imaginaires pures.
Si z = i ; z2 = -1 ; z3= -i ; z4= 1 ; 1-i-5+i+4 = 0 est vérifié.
Si z = -i ; z2 = -1 ; z3=+i ; z4= 1 ; 1+i-5-i+4 = 0 est vérifié.
(E) s'écrit : (z+i)(z-i)(z2+z+4)=0 ; (z2+1)(z2+z+4)=0 ;
Solutions de : z2+z+4
= 0. Le discriminant étant négatif, il n'y a pas de solutions réelles,
mais deux solutions du type z = a+ib avec a et b non nuls.
Question 13
L'équation (E) admet exactement :
A. aucune racine réelle. Vrai.
B. une racine réelle.
C. deux racines réelles.
D. trois racines réelles.
E. quatre racines réelles.
Question
14
Le nombre de solutions distinctes de (E) de la forme a+ib avec a et b réels non nuls est exactement :
A. zéro
B. une.
C. deux. Vrai
D. trois.
E. quatre.
.
|
|
Complexes et géométrie.
12. L'écriture
exponentielle de 2-2i est :
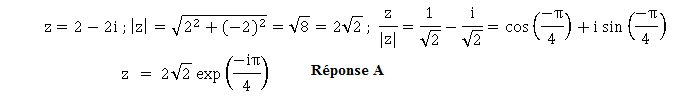
Dans les 4 items suivants on considère
les nombres complexes z1 = 2 exp(ip/9) et z2 = -2 exp(-ip/9)
13. z127
est
A. un réel strictement positif
;
B. un réel strictement
négatif ; vrai ;
C. un
imaginaire pur
;
D. nul ;
E. aucune des propositions
précédentes.
227 exp((ip/9 x27) = 227 exp((3ip)
=227 exp((ip)
= -227 .
14. z118 est
A. un réel strictement positif
;
vrai ;
B. un réel strictement négatif ;
C. un
imaginaire pur
de partie imaginaire strictement positive;
D. un
imaginaire pur
de partie imaginaire strictement négative;
E. aucune des propositions
précédentes.
218 exp((ip/9 x18) = 218 exp((2ip)
= 218.
.
15. On a :
A. z1 = z2; B.
z1 = - z2;
C.
z1 = conjugué de z2;
D. z1 = -conjugué de z2;
E. aucune des propositions
précédentes. Vrai.
z1 = 2( cos ( p/9)
+i sin (p/9)
; z2
= -2( cos ( -p/9)
+i sin (-p/9)
=
2( -cos ( p/9) +i
sin (p/9).
15. On a :
A. z1 = z2; B.
z1 = - z2;
C. z1 =
conjugué de z2;
D. z1 = -conjugué de z2;
E. aucune des propositions
précédentes. Vrai.
16. z1 +z2
est un :
A. reél strictement positi f; B.
un réel strictement
négatif ;
C. un imaginaire pur
de partie imaginaire strictement positive ; vrai
D. un imaginaire pur de
partie imaginaire strictement négative ;
E. aucune des propositions
précédentes. Vrai.
2( cos ( p/9) +i sin (p/9)+2( -cos ( p/9) +i sin (p/9)
=4isin
(p/9)~2,47
i.
17. L'écriture
algébrique du nombre complexe z est :
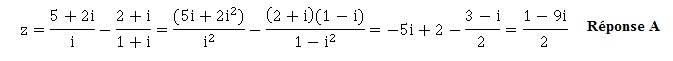
|
|
On
se place dans le plan complexe d'origine O.
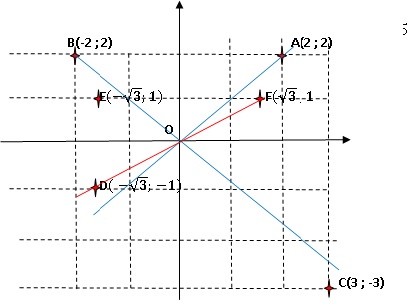
Affixe de A : zA = 2+2i ; affixe de B : zB =-2+2i ,
affixe de C : zC = a-3i avec a un réel ;
affixe de D : zD = -3½-i ; affixe de E : zE = -3½+i
; affixe
de F : zF = 3½+i.
18. Le triangle AOC est rectangle en
O si a est égal à :
:
A. 2 ; B. 3 vrai ; C. -2 ; D.
-3; E. aucune
des propositions précédentes.
OA2 =22+22 = 8 ; OC2
=a2+(-3)2 = 9+a2 ; AC2 =
(a-2)2 +(-3-2)2=a2-4a+29.
OA2
+OC2
=AC2
; 17+a2
=a2-4a+29
; 4a=12 ; a=3.
On prend pour la suite la valeur de a
telle que le triangle OAC est rectangle en O.
19.
On
a :
A.
Le triangle AOB est rectangle en A
; B. Le
triangle AOB est rectangle en O vrai
; C.
Le triangle DOE est rectangle en D ;
D. Le triangle AOB
est équilatéral ; E. aucune
des propositions précédentes.
20.
On
a :
A.
Le triangle AOF est rectangle ; B. Le
triangle DOE est rectangle en O ;
C.
Le triangle AOF est isocèle ;
D. Le triangle DOE
est équilatéral ; E. aucune
des propositions précédentes. Vrai.
21.
On
a :
A.
Le triangle AOC est équilatéral ; B. Le
triangle DOB est rectangle ; C.
Le triangle AOB est isocèle vrai ;
D. Le triangle AOB
est équilatéral ; E. aucune
des propositions précédentes.
OA2 =22+22 = 8 ; OB2
=(-2)2+22 = 8 ; AB2 = (-4)2
+(0)2=16.
22. On a :
A.
Les points A, O et D sont alignés
; B. Les
points B, O et C sont alignés ;
C.
Les points E, O et B sont alignés ;
D. Les
points A, O et F sont alignés ; E. aucune
des propositions précédentes. Vrai.
23.
On
a :
A.
Les points A, O et E sont alignés
; B. Les
points F, O et D sont alignés vra i;
C.
Les points E, O et F sont alignés ;
D.Les
points B, O et D sont alignés ; E. aucune
des propositions précédentes.
Exercice 3.
On considère le nombre complexe z = 5 i exp(ip/8) :
10. Le module de z est :
A. 1 ; B. 5, vrai. C. -5 ;
D. 25. E. 5½.
11. L'argument de z est :
A. -p/8. B. p/8. C. 5p/8, vrai. D. 3p/8 ; E. -5p/8.
z = 5 exp(ip/2) exp(ip/8) =5 exp(i(p/2+p/8)).
12. z2 est :
A. un réel strictement positif
;
B. un réel strictement
négatif ;
C. un
imaginaire pur de partie imaginaire strictement positive
;
D. un
imaginaire pur de partie imaginaire strictement négative ;
E. aucune des propositions
précédentes vrai.
z2 = 25 exp(5ip/4) =25 ( cos(5p/4)+ i sin(5p/4)) .
13. arg(z2)
est
A. 5p/4, vrai
; B. p/4 ;
C. 0
; D. p/ 2 ; E.2 5p/ 64.
Exercice 4.
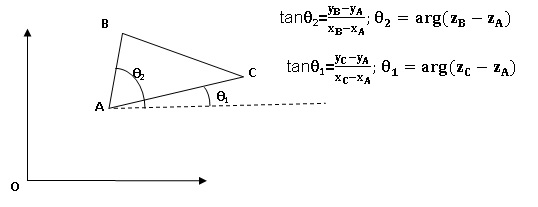
On considère un triangle ABC quelconque non aplati. Les points A, B et C ont pour affixes respectives zA, zB et zC.
14. L'angle CAB est obtenu en calculant :
A. arg(zB)-arg(zC) ;
B. arg(zB) /arg(zC );
C. [ arg(zB -zA)] / [arg(zC-zA)];
D. [ arg(zB)-arg(zA)] / [arg(zC)-arg(zA)];
E. arg(zB -zA) - arg(zC-zA). Vrai.
Exercice 5.
Soient
A et b deux points non confondus et I le milieu du segment [AB]. Dans
le plan complexe, les points A, B et I, ont pour affixes respectifs zA, zB, zI.
15.
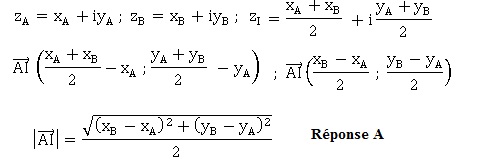
Exercice 6.
16. L'affixe de B est alors :
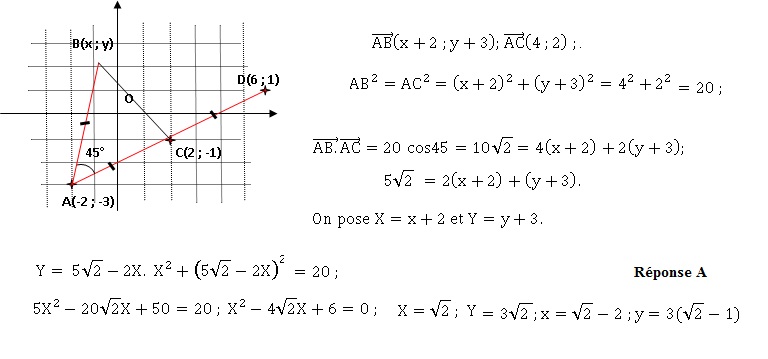
17. L'affixe de D est :
A. 2-i ; B. 6+i vrai ; C. -2i ; D. 4; E. aucune
des propositions précédentes.
C milieu de [AD] ; xC = 0,5(xA +xD) ; xD=2xC -xA =4-(-2)=6.
yC = 0,5(yA +yD) ;yD=2yC -yA =-2-(-3)=1.
|
|