Chimie,
concours TSPEI 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Les alcools.
A. Ethanol et saccharose.
Le bioéthanol peut être obtenu par fermentation du saccharose C12H22O11
extrait de la betterave sucrière. Le pourcentage moyen de
saccharose dans la betterave est de 20 %. L'équation de la réaction de
fermentation alcoolique du saccharose s'écrit :
C12H22O11 aq + H2O(l) ---> 4C2H6O aq + 4 CO2 aq.
1.1. Donner la formule semi-développée de l'éthanol.
CH3-CH2 OH.
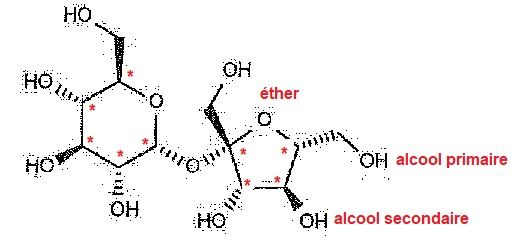
1.2 Quels sont les groupes fonctionnel présents dans la molécule de saccharose ?
1.3.
Définir un atome de carbone asymétrique et faire apparaître les
atomes de carbone asymétriques dans la molécule de saccharose.
Un atome de carbone asymétrique est lié à 4 atomes ou groupes d'atomes différents.
1.4. Calculer la masse mS de saccharose contenu dans une betterave sucrière de masse m = 2,0 kg.
mS = 2,0 x 0,20 = 0,40 kg.
1.5. Déterminer la masse mE puis le volume VE d'éthanol obtenu par fermentation alcoolique.
Quantité de matière de saccharose n = mS / M(saccharose) = 400 /342 = 1,17 mol.
Quantité de matière d'éthanol : 4n = 4 x 1,17 = 4,68 mol.
Masse d'éthanol : 4,68 m(éthanol) = 4,68 x 46 = 215,2 g.
Volume d'éthanol = masse d'éthanol / masse volumique de l'éthanol = 215,2 / 0,789 ~273 mL.
1.6.
Un véhicule consomme V = 5,0 L de carburant aux 100 km et parcourt 20
000 km / an. Déterminer la masse de betterave sucrière nécessaire à un
fonctionnement de ce véhicule en bioéthanol.
Volume annuel de bioéthanol : 5,0 x 200 = 1000 L.
2 kg de betterave sucrière fournissent 0,273 L de bioéthanol.
Masse de betterave : 1000 / 0,273 x 2 = 7,3 103 kg.
B. Prépartation de l'éthanol.
Hydratation de l'éthène CH2=CH2 en milieu acide.
1.7. La molécule d'éthène présente-t-elle l'isomérie Z / E ? Justifier.
Cette molécule ne présennte pas d'isomérie Z / E ; les deux atomes de carbone portent les même substituants.
1.8. Ecrire l'équation de la réaction d'hydratation de l'éthylène.
CH2=CH2 + H2O ---> CH3-CH2 OH.
1.9 A quelle grande classe de réaction en chimie organique appartient cette réaction ? En donner le mécanisme détaillé.
Addition sur une double liaison C=C.
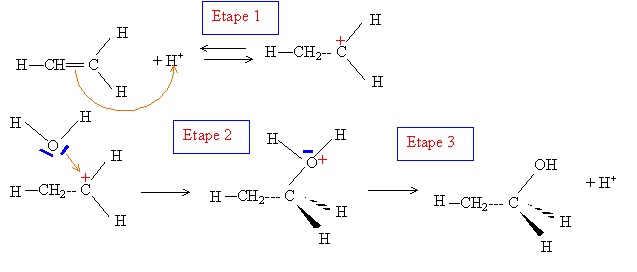
On s'intéresse à l'asppect thermodynamique de la réaction. Elle s'effectue à 600 K sous une pression de 70 bars.
1.10.
Calculer l'enthalpie standard de la réaction et de l'entropie à 298 K.
Commenter les signes de ces grandeurs. Justifier le choix de la
pression 70 bars.
DH°=DfH°(éthanol gaz) - DfH°(eaul gaz) - DfH°(éthène gaz) = -235,1 -(-241,8)-(52,5) = -45,8 kJ / mol. ( réaction exothermique).
DS°=S°(éthanol gaz) - S°(eaul gaz) - S°(éthène gaz) = 282,7 -188,8-219,6 = -125,7 J / mol / K.
L'entropie diminue, le nombre final de molécules de gaz est inférieur au nombre initial de molécules.
La réaction dans le sens direct est favorisée par une augmentation de pression.
1.11. Calculer la constante d'équilibre à 600 K.
DG°= DH°-T S° = -45,8 103 -600 (-125,7) = 2,86 104.
DG°= -RT ln K ; ln K = -2,86 104 /(8,314 x600) = -5,94 ; K = 2,6 10-3.
1.12 On introduit une mole d'éthène et une mole d'eau. Déterminer la composition du mélange à l'équilibre.
|
Avancement (mol)
|
éthène
|
+eau
|
éthanol
|
initial
|
0
|
1
|
1
|
0
|
à l'équilibre
|
x
|
1-x
|
1-x
|
x
|
Pression partielle éthanol : Px / (2-x) ; pression partielle de l'eau (g) = pression partielle éthène : P(1-x) / (2-x).
K =x (2-x) / (P(1-x)2).
2x-x2 = 2,6 10-3 x 70(1-x)2= 0,182(1-x)2.
x2-2 x+0,153 =0 ; solution x ~ 0,08.
C. Oxydation de l'éthanol.
Le cuivre est utilisé comme catalyseur. Le cuivre cristallise dans le système cubique à face centrée.
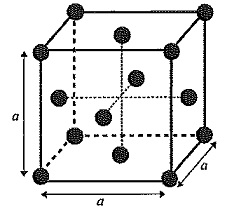 a = 3,60 10-10 m. a = 3,60 10-10 m.
1.13 Déterminer le nombre d'atomes de cuivre par maille.
Ceux qui sont sur les sommets du cube compte pour 1 / 8 ( ils appartiennent à 8 mailles)
Ceux qui sont au centre des faces comptent pour 1 /2.
1 / 8 x8 + 6 x 0,5 = 4.
1.14. Calculer la masse volumique du cuivre.
Masse de la maille : m = 4 M(Cu) / NA = 4 x0,0635 / (6,02 1023) =4,2 10-25 kg.
Volume de la maille : V = a3 = 4,67 10-29 m3.
Masse volumique du cuivre : m / V ~ 9,0 103 kg m-3.
|
|
Le dioxyde de carbone.
2.1. Donner la structure électronique de l'élément carbone et de l'élément oxygène.
C : 1 s2 2s2 2p2 ; O : 1 s2 2s2 2p4 .
2.2. En déduire la formule de Lewis du dioxyde de carbone.
2.3. Déterminer la géométrie de cette molécule.
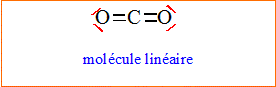 L'atome
de
carbone central est du type AX2. L'atome
de
carbone central est du type AX2.
Le processus de dissolution du dioxyde de carbone dans l'eau limite la
concentration de celui-ci dans l'atmosphère. l'équation de la
réaction s'écrit :
CO2(g) = CO2 aq. K° = 3,39 10-2 à 298 K.
2.4. La pression partielle en dioxyde de carbone gazeux danns l'atmosphère terrestre est p(CO2) = 4,00 10-4 bar. En déduire la valeur de la concentration en CO2 aq à 298 K.
K° = [CO2 aq] / p(CO2) ; [CO2 aq] = 4,00 10-4 x 3,39 10-2 = 1,356 10-5 ~1,36 10-5 mol / L.
La loi d'évolution de la constante d'équilibre en fonction de la température est donnée par :
ln(K°) = 2627 / T -12,2.
2.5. En déduire si
la dissolution du dioxyde de carbone dans l'eau est favorisée à
haute ou faible température. Quelles zones océaniques de la planète
stockent le mieux le dioxyde de carbone ? Quel est l'effet du
réchauffement climatique sur l'efficacité de ce stockage ?
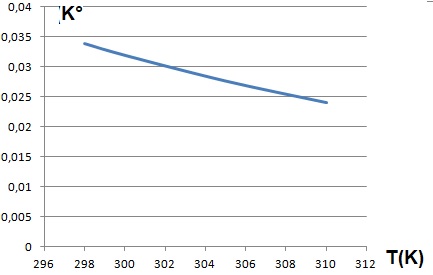
Si T augmente, K° diminue. La dissolution du dioxyde de carbone est favorisée à basse température.
La solubilité de CO2,
augmente quand la température de l’eau diminue ( régions polaires ).
L’eau chargée en gaz dissout ayant une densité plus grande que l’eau
chaude descend au fond de la mer en emportant le CO2dissout.
Le quotient initial (Qr i =[CO2aq]i /PCO2 i ) de réaction diminue si la pression partielle en CO2 augmente ( à température constante) .
Qr i < K°, l'équilibre est déplacé dans le sens direct, solubilisation du gaz.
2.6. Déterminer la valeur numérique de l'enthalpie standard de la réaction de dissolution. Que conclure sur son signe ?
DrH° = DfH°(CO2aq) -DfH°(CO2 g) =-413,8 -(-393,5)= -20,3 kJ /mol.
DrH° < 0, réaction exothermique défavorisée dans le sens direct par une augmentation de température à pression constante.
Dans l'eau le dioxyde de carbone se présente sous la forme d'un diacide CO2, H2O.
pKa1 ( CO2,H2O / HCO3-)=6,4 et pKa1 ( HCO3-/CO32-)=10,3.
2.7. Ecrire les deux demi-équations acido-basiiques correspondant à ces deux couples.
CO2,H2Oaq +H2O(l)= HCO3- aq+ H3O+aq.
HCO3-aq +H2O(l)=CO32-aq+ H3O+aq.
2.8 Tracer le diagramme de prédominance des espèces en fonction du pH.
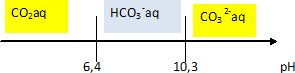
2.9. Le pH de l'eau de mer est compris entre 8,1 et 8,3. En déduire l'espèce prédominante.
HCO3- aq prédomine .
2.10. Prévoir qualitativement l'influence de la dissolution du dioxyde de carbone sur le pH des océans.
CO2,H2Oaq +H2O(l)= HCO3- aq+ H3O+aq.
Si CO2,H2Oaq croît, alors cet équilibre est déplacé dans le sens direct ; H3O+aq augmente et le pH de l'eau de mer diminue.
Une méthode de valorisation du dioxyde de carbone est de le transformer
en acide méthanoïque par électrolyse. Le dioxyde de carbone dissout est
réduit à la cathode et on observe un dégagement de dioxygène à l'anode.
E°(CO2 / HCOOH) = -0,20 V ; E°(O2 / H2O) = 1,23 V.
2.11. Ecrire les demi-équations des réactions se produisant à kl'anode et à la cathode.
Oxydation à l'anode ; H2O = ½O2 +2H+ + 2e-.
Réduction à la cathode : CO2 +2H+ + 2e- = HCOOH.
2.12. En déduire l'équation de la réaction d'électrolyse.
H2O + CO2 = ½O2 +HCOOH.
|
|
Oxydes d'azote. Dosage des nitrates.
On faiit barboter un volume VG = 1,0 m3 de gaz d'échappement dans un volume VE = 1,0 L d'eau. L'équation de la transformation chimique s'écrit :
N2O5(g) +3H2O(l) ---> 2NO3-aq + 2H3O+aq.
La solution S0 est placée en présence de cadmium métallique Cd. Les ions nitrates sont transformés en nitrites NO2-.
3.1. Déterminer les nombres d'oxydation de l'élément azote dans les ions nitrates et nitrites.
Nitrate : n.o(N) -3 x(-2) = -1 ; n.o(N) = + V.
Nitrite : n.o(N) -2 x(-2) = -1 ; n.o(N) = + III.
3.2. Ecrire les demi-équations d'oxydoréduction correspondant aux couples Cd2+ / Cd et NO3-aq / NO2-aq.
Cd = Cd2+ aq+ 2e-.
NO3-aq +2H+aq + 2e-= NO2-aq +H2O(l)
3.3 E°(Cd2+ / Cd) = -0,46 V ; E°(NO3-aq / NO2-aq) = 0,94 V. En déduire que la réaction entre les ions nitrates et le cadmium est thermodynamiquement favorisée.
NO3-aq est l'oxydant le plus fort et Cd est le réducteur le plus fort. La réaction entre les ions nitrates et le cadmium est thermodynamiquement favorisée.
3.4. Ecrire l'équation de la réaction entre les ions nitrates et le cadmium.
NO3-aq +2H+aq + Cd = NO2-aq +H2O(l) +Cd2+ aq.
K = [Cd2+ aq] [NO2-aq] / ([NO3-aq] [H+aq]2).
3.5. Calculer la constante K de la réaction.
E1 = E°(Cd2+ / Cd)+0,03 log [Cd2+ aq].
E2 = E°(NO3-aq / NO2-aq) +0,03 log ([NO3-aq] [H+aq]2 /[NO2-aq] ).
A l'équiibre : E1 = E2 ; E°(Cd2+ / Cd)+0,03 log [Cd2+ aq] = E°(NO3-aq / NO2-aq) +0,03 log ([NO3-aq] [H+aq]2 /[NO2-aq] ).
0,03 log K = E°(NO3-aq / NO2-aq) - E°(Cd2+ / Cd) ;
log K = (0,94 + 0,46) / 0,03 6,7 ; K ~ 4,6 1046.
On prélève précisément V0= 50,0 mL du filtrat que l'on
introduit dans une fiole jaugée de volume V = 100,0 mL. On y
ajoute une petite quantité du réeactif R. On complète au trait de jauge
avec de l'eau distillée. La solution se colore en rose. la réaction
entre les ions nitrites et R est une réaction totale mole à mole.
3.6 Préciser le nom de la verrerie à utiliser pour prélever les 50,0 mL de filtrat.
Pipette jaugée de 50 ,0 mL..
3.7. Faire le schéma d'une fiole jaugée.
On prépare une gamme étalon à partir de solutions S1, S2, S3, S4 et S5 de concentrations connues en ion nitrate auquelles on a appliqué le même protocole que la solution S0.
On règle la longueur d'onde du spectrophotomètre à 540 nm. On fait le
blanc avec de l'eau distillée et on mesure les absorbances des
solutions.
Solution
|
eau distillée
|
S1
|
S2
|
S3
|
S4
|
S5
|
S0
|
Concentration massique en ion nitrate (mg / L)
|
0
|
0,10
|
0,20
|
0,30
|
0,40
|
0,50
|
?
|
Absorbance
|
0
|
0,063
|
0,127
|
0,190
|
0,254
|
0,317
|
0;231
|
3.8. Justifier le choix de la longueur d'onde à 540 nm.
La solution doit présenter un maximum d'absorption à la longueur d'onde choisie.
La solution étant rose, l'absorption sera maximale pour la couleur complémentaire du rose.
3.9. Qu'appelle t-on faire le blanc ?
On règle l'absorbance à zéro, en plaçant dans la cuve le solvant seul.
3.10. Tracer le graphe A = f( concentration C en ion nitrate).
3.11. Rappeler la loi de Beer-Lambert ? Est-elle vérifiée ?
3.12. Déterminer graphiquement la concentration massique C0 en ion nitrates dans la solution S0.
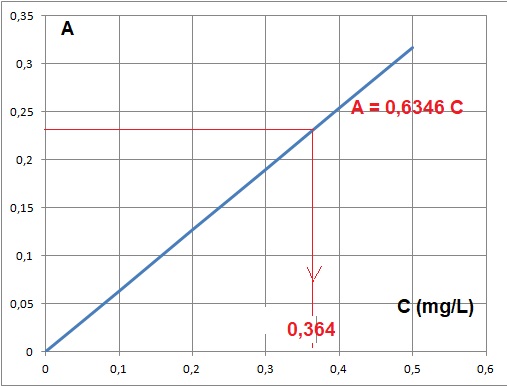
Pour de faibles concentrations, l'absorbance et la concentration de la substance absorbante sont proportionnelles.
La loi de Beer est bien vérifiée, le graphe est une droite passant par l'origine.
On prélève précisément V0= 50,0 mL du filtrat que l'on
introduit dans une fiole jaugée de volume V = 100,0 mL. On y
ajoute une petite quantité du réeactif R. On complète au trait de jauge
avec de l'eau distillée.
En tenant compte du facteur de dolution C0 = 0,364 x2 = 0,728 mg / L.
Concentration molaire en ion nitrate : C0/ M(Nitrate) =0,728 / (14+3 x16) = 0,0117 mmol / L.
3.13 En déduire la concentration C en N2O5 en mg m-3 de gaz d'échappement.
N2O5(g) +3H2O(l) ---> 2NO3-aq + 2H3O+aq.
Concentration molaire en N2O5 : 0,5 x 0,0117 = 0,00587 mmol / L.
Concentration massique en N2O5 : 0,00587 M(N2O5 ) = 0,00157 x(28 +5x16) ~0,634 mg /L de solution soit 0,634 mg dans 1 m3 de gaz d'échappement.
|
|