Physique,
concours TSPEI 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Centrale nucléaire.
Une des réactions nucléaires s'écrit :
23592U +10n ---> 94ZSr +A54Xe +310n.
1.1. Quel nom donne t-on à ce type de réaction nucléaire ?
Réaction de fission.
1.2 Déterminer A et Z en précisant les lois de conservation utilisées.
Conservation de la charge : 92 = Z+54 ; Z =38.
Conservation du nombre de nucléons : 235+1 = 94+A+3 ; A =139.
1.3. Enoncer la relation d'équivalence masse-énergie en précisant les unités des grandeurs utilisées.
E = m c2.
E ( joule) ; m ( kg) ; c = 3 108 m s-1.
1.4. Exprimer en fonction des masses des particules et des noyaux, la variation d'énergie de masse DE au cours de cette réaction.
DE = ( m(94ZSr) + m(A54Xe)+2m(10n)-m(v))c2.
1.5. Calculer sa valeur en J puis en MeV.
DE = ( 93,8946 + 138,889+2x1,00866-234,9935) x1,66054 10-27 x (3,00 108)2= -2,878 10-11 J.
-2,878 10-11 / (1,6 10-13)~ -180 MeV.
Parmi les sous-produits des centrales nucléaires, l'iode 13153I se désintègre en Xénon 131 13154Xe..
1.6. Ecrire l'équation de désintégration correspondante et préciser le type de cette désintégration.
13153I ---> 13154Xe + 0-1e, radioactivité de tipe ß-.
L'activité
( Bq) d'une substance radioactive est définie par A(t) = -dN(t) / dt où
N est le nombre de noyaux radioactifs à la date t.
1.7. Rappeler la loi de décroissance radioactive de l'activité.
A(t) = A0 exp(-lt) avec lt½ = ln 2.
1.8. Au bout de 81 jours, l'activité d'un échantillon d'iode 131 est divisée par 1000. Déterminer le temps de demi-vie t½ de l'iode 131.
A0 / A(t) = 1000 = exp(81l) ; ln(1000) = 81 l ; l = 8,528 10-2 j-1.
t½ = ln 2 / (8,528 10-2) ~8,1 jours.
Une centrale nucléaiire produit une puissance électrique Pe
= 900 MW. L'eau du circuit secondaire décrit un cycle ditherme moteur
assimilé dans cette partie à un cycle de Carnot fonctionnant de manière
réversible entre deux sources de température TC et TF supposées constantes avec TC > TF.
QC =Q et QF =Q' représentent les transferts
thermiques avec respectivement la source chaude et la source froide et
W le travail échangé entre la machine et le milieu extérieur.
1.9 Préciser les signes de QC, QF et W.
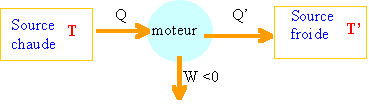
QC =Q >0 ; QF =Q' <0.
1.10. A partir du premier principe, exprimer le travail W en fonction de QC et QF.
Sur le cycle W + QC +QF = 0 ; W = -QC-QF.
1.11. A partir du second principe, donner l'expression de QF en fonction de QC, TC et TF.
Sur le cycle réversible : QC / TC + QF / TF = 0 ; QF = -QC TF / TC.
1.12 Définir puis exprimer en fonction de TC et TF le rendement de Carnot n.
h = | W / QC| =| (-QC-QF) / QC| = |-1-QF / QC | =|-1-QF / QC | = 1-TF/TC.
1.13 Calculer ce rendement si TC = 543 K et TF = 303 K.
1-303 / 543 ~0,44 ( 44 %).
1.14. L'eau du circuit secondaire reçoit une puissance thermique Pt
= 2785 MW. La puissance mécanique de la turbine est intégralement
convertie en puissance électrique. Calculer le rendement réel de
l'installation et commenter.
Pe / Pt = 900 / 2785 ~0,32, valeur inférieure au rendement de Carnot.
Dans la réalité, les transformations ne sont pas réversibles.
|
|
Production hydraulique d'électricité.
La puissance Pe de la turbine Pelton est donnée par :
Pe = K ra Sß Vg R W (1-WR / V).
K est sans dimension.
r est la masse volumique de l'eau.
S aire de la section droite du jet.
V vitesse avec laquelle le jet sort de l'injecteur.
W vitesse de rotation de la turbine.
R rayon utile de la roue sur laquelle sont fixés les augets.
2.1. Donner les unités de ces grandeurs.
r (kg m-3) ; S (m2) ; .V ( m s-1) ; W ( rad s-1); R (m).
2.2. Déterminer les coefficients a, ß, g par analyse dimensionnelle.
Puissance : J s-1 = N m s-1 = kg m s-2 m s-1 = kg m2 s-3.
kga m-3a m2ß mg s-g m s-1 =kg m2 s-3.
On identifie : a = 1 ; g = -2 ; ß = 1,5.
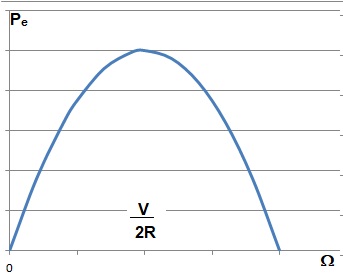
2.3. Montrer que la puissance de la turbine est maximale pour une vitesse de rotation W que l'on exprimera en fonction de K, r, S, V et R.
On pose A =K ra Sß Vg R > 0 et B = R / V > 0 ; Pe = AW (1-WB) = -AB W2+AW ; équation d'une parabole de sommet [ V / (2R) ; A V / (4R) ].
On peut aussi dériver Pe par rapport à W et on annule cette dérivée.
u = A W et v =(1-WR / V) ; u' =A ; v'= -R/V.
u'v + v'u = A(1-WB) - R / V A W= 0.
1-WB=B W ; 1 =2 R W / V ; W = V / (2R).
La régulation de la puissance délivrée par la turbine est possible par
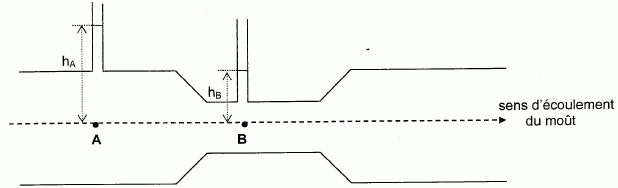
le contrôle du débit Q de l'eau. Pour mesurer ce débit, on insère dans
la conduite un tube de Venturi horizontal composé de deux parties
cylindriiques de section SE et SS réunies
entre elles par un manchon conique. L'eau s'écoule en régime
stationnaire et on suppose les pertes de charge négligeables.
2.4
Montrer que le débit volumique à travers une section droite peut
s'écrire Q = SV où v v représente la vitesse du fluide et S la
section de la conduite.
Q = volume ( m3) / temps ( s) =section (m2) x longueur (m) / temps (s).= section (m2) x vitesse ( m s-1).
2.5. Ecrire la conservation du débit volumique entre les sections droites SE et SS.
Q =SE vE = SS vS.
2.6. Comparer, en justifiant, vE vitesse d'entrée de l'eau et VSPS-PE =r(VE2 -VS2) /2 vitesse de l'eau en sortie.

SS < SE, donc VS > VE.
Le théorème de Bernoulli entre deux points A et B s'écrit :
pA / (rg) +VA2 /(2g) +zA = pB / (rg) +VB2 /(2g) +zB .
2.7. Exprimer la variation de pression DP = PS-PE.
PS-PE =r(VE2 -VS2) /2 + rg(zE -zS).
La conduite étant horizontale : PS-PE =r(VE2 -VS2) /2.
DP =r Q2(1 /SE2 -1/ SS2) /2.
2.8. Expliquer comment une mesure judicieuse de pression permet de déterminer le débit volumique.
Le tube de Venturi crée une dépression DP proportionnelle à Q2v.
|
|
Bobine électrique.
On dispose d'une bobine d'auto-induction dont on souhaite connaître les caractéristiques résistance r et inductance L.
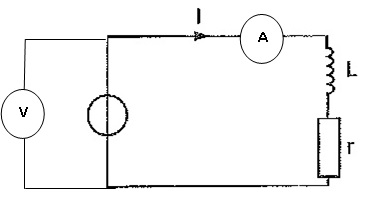
Le générateur délivre une tension U1 qui impose dans le circuit un courant d'intensité I1 en régime permanent.
3.1. Reproduire la figure avec les appareils de mesures qui permettront de mesurer les valeurs de U1 et I1.
3.2. U1=6,60 V et I1
= 0,88 A. Les calibres du voltùètre sont 200 mV, 2 V, 20 V, 200 V et
ceux de l'ampèremètre sont 200 µA, 2000 µA, 20 mA, 200 mA et 2 A. Quels
sont les calibres que l'on doit utiliser ? Déterminer r.
20 V et 2 A.
r = U1 / I1 = 6;60 / 0,88 = 7,5 ohms.
Le
générateur délivre maintenant une tension alternative sinusoïdale
de fréquence f = 50 Hz. On effectue sur le mode AC les mêmes
mesures que précédemment : U2 = 6,7 V ; I2 = 0,32 A.
3.4 Mesure t-on une amplitude ou une grandeur efficace ?
On mesure une grandeur efficace.
3.5. Donner l'expression de l'impédance complexe puis de l'impédance réelle du dipôle r, L.
z = r + jLw avec w = 2 p f ; Z =(r2 + (Lw)2)½ .
3.6 En déduire la valeur de L.
Z = 6,7 / 0,32 = 20,94 ohms.
20,942 =7,52 + (314L)2) .
(314L)2) =382,12 ; L = 0,062 H.
Le générateur délivre un échelon de tension : u(t) = 0 pour t <0 et u(t) = E pour t > 0.
3.7. Etablir l'équation différentielle régissant l'intensité i(t).
E = r i + Ldi /dt. (1)
3.8. Définir puis calculer la constante de temps t.
t = L / r = 0,062 / 7,5 =8,3 10-3 s = 8,3 ms.
3.9. Donner la solution de l'équation différentielle.
Solution générale de r i + Ldi /dt = 0 : i(t) = A exp(-r / L t) avec A une constante.
Solution particulière de (1) : i = E / r ( régime permanent).
Solution générale de (1) : i(t) = A exp(-r / L t) +E / r.
i(0) = 0 d'où A = -E / r.
i(t) = E /r(1-exp(-r / L t)).
|
|