Mathématiques,
concours TSPEI 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Premier exercice.
Une
enquète est menée pour étudier le nombre de clients d'un site de vente
en ligne. Au cours du premier mois de l'enquète, 8000 personnes ont
effectué des achats sor le site. On admet que chaque mois, 70 % des
clients du mois précédent restant fidèles au site et que 3000
nouveaux clients apparaissent.
Soit n un entier naturel non nul.
On note Un le nombre de clients ayant effectué des achats au cours du nième mois de l'enquète. Ainsi U1 = 8000.
1.a. Calculer U2 et U3.
U2 = 8000 x0,7 +3000 = 8600.
U3 = 8600 x0,7 +3000 = 9020.
1.b Montrer que pour tout entier naturel non nul, Un+1 = Un x0,7 +3000.
Nombre de clients au cours du mois n+1 : 70 % des clients du mois n restent fidèles et 3000 nouveaux clients apparaissent.
Un+1 = Un x0,7 +3000.
2.a. On considère la suite (Vn) définie, pour tout entier naturel n non nul, par : Vn = 10000-Un.
Calculer V2 et V3.
V2 = 10000-8600 = 1400.
V3 = 10000-9020 = 980.
2.b. Montrer que (Vn) est une suite géométrique dont on donnera le premier terme et la raison.
Vn+1 = 10000 -(0,7 Un+3000) =7000-0,7 Un.
Vn+1 =0,7( 10000-Un) = 0,7 Vn.
(Vn) est une suite géométrique de raison 0,7 et de premier terme V1 = 2000.
3. Exprimer Vn, puis Un en fonction de n.
Vn = 0,7n-1 x 2000.
Un = 10000- 0,7n-1 x 2000.
4. Quelle et la limite de la suite (Un) quand n tend vers l'infini ?
0 < 0,7 < 1, donc 0,7(n+1) tend vers zéro quand n tend vers plus l'infini.
Un tend vers 10000 quand n tend vers plus l'infini.
.
|
|
Deuxième exercice.
Soit f la fonction définie sur [0 ; +oo [ par :
f(x) = x2-xln(x) si x différent de zéro et f(0) = 0.
1.a. Calculer f(1) et f(0,5).
f(1) = 1-ln(1) = 1.
f(0,5) = 0,52 -0,5 ln(0,5) =0,25 + 0,5 ln(2).
1.b. Déterminer la limite de f en 0+ et interpréter.
f(x) = x2(1 -ln(x) / x).
Quand x tend vers 0+ : ln(x) / x tend vers moins l'infini.
1 -ln(x) / x tend vers plus l'infini.
f(x) tend vers zéro.
1.c. Déterminer la limite de f(x) quand x tend vers plus l'infini.
Par croissance comparée, ln(x) / x tend vers zéro.
f(x) tend vers plus l'infini.
2. Calculer f '(x) et f"(x).
On pose u = x et v = ln(x) ; u' = 1 et v' = 1 /x ; u'v+v'u = ln(x) +1.
f '(x) = 2x-(ln(x)+1).
f "(x) = 2 -1 /x.
3. Etudier les variations de f '(x) et en déduire le tableau de variations de f.
f "(x) s'annule pour x = 0,5.
f "(x) est négative pour x appartenant à [0 ; 0,5[ ; f '(x) est décroissante sur [0 ; 0,5[.
f '(0,5) = ln(2) ; f '(x) tend vers l'infini si x tend vers 0+.
f '(x) est donc positive sur [0 ; 0,5[ et f(x) est croissante sur cet intervalle.
f "(x) est positive pour x appartenant à [0,5 ; +oo[ ; f '(x) est croissante sur [0,5 ; +oo[.
f '(0,5) = ln(2) ; f '(x) tend vers l'infini si x tend vers plus l'infini.
f '(x) est donc positive sur [0,5 ; +oo[ et f(x) est croissante sur cet intervalle.
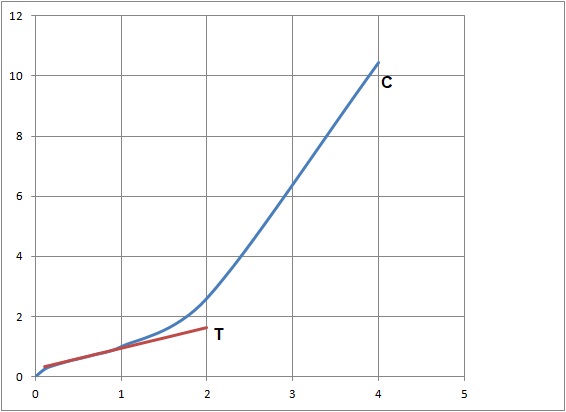
Soit C la courbe représentative de f.
4. Ecrire une équation de la tangente (T) à la courbe C au point I d'abscisse 0,5.
Coefficient directeur de (T) : f '(0,5) = ln(2).
(T) passe par I(0,5 ; 0,25 +0,5 ln2).
0,25 +0,5 ln(2) = 0,5 ln(2) + b ; b =0,25.
y = ln(2) x +0,25.
5. Déterminer la limite en 0+ de f(x) / x. Interpréter géométriquement.
f(x) / x= x-ln(x)
-ln(x) tend vers plus l'infini et x tend vers zéro.
f(x) / x tend vers plus l'infini quand x tend vers 0+.
L'axe des ordonnées est asymptote à la courbe représentative de f(x) / x.
6. Construire C et (T)
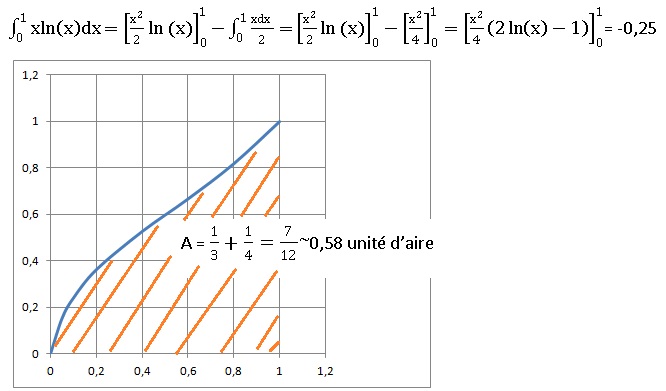
7. Calculer en cm2, l'aire du domaine compris entre l'axe des abscisses, la courbe C et les droites d'équations x=0 et x = 1.
Primitive de x2 : x3 / 3.
Primitive de x ln(x) :
|
|
Troisième exercice.
Suite à la publication d'offres d'emploi, une entreprise a reçu
de nombreuses candidatures et étudie celles-ci selon deux critères, le
niveau scolaire et l'expérience professionnelle.
Parmi les personnes ayant déposé un dossier on constate que :
60 % ont un niveau inférieur ou égal au baccalaurat et 40 % un niveau supérieur.
20 % sont sans expérience professionnelle..
Parmi les personnes ayant un niveau supérieur au baccalaurat, 15 % sont sans expérience professionnelle.
1.a. On prélève au hasard un dossier de candidature parmi les dossiers reçus.
Quelle
est la probabilité que ce dossier corresponde à une personne de niveau
supérieur au baccalauréat et sans expérience professiionnelle ?
On définit les événements suivants :
D : " niveau inférieur ou égal au baccalauréat".
C : " sans expérience professionnelle".
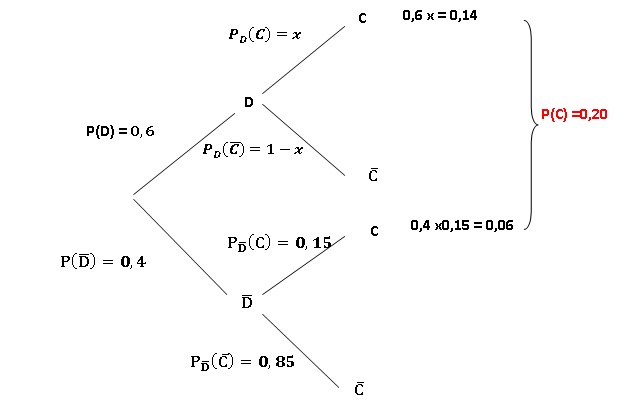
b.
Sachant que le dossier prélevé correspond à une personne sans
expérience professionnelle, calculer la probabilité que celle-ci ait un
niveau supérieur au baccalaurat.
PC(non D)=P(non D n C) / P(C) =0,06 /0,2 =0,3.
c. Sachant
que le dossier prélevé correspond à une personne ayant un niveau
inférieur au baccalauréat, calculer la probabilité que celle-ci soit
sans expérience professionnelle.
PD(C)=P(D n C) / P(D) =0,14 /0,6 =14/60=7 / 30 ~0,23.
2. Le directeur des
ressources humaines choisit au hasard 3 dossiers de candidatures
parmi tous les dossiers reçus. En justifiant, déterminer la probabilité
que, parmi ces 3 dossiers, il y ait au moins un dossier correspondant à
une personne sans expérience professionnelle.
Au moins 1 signifie : 1 ou 2 ou 3.
1-probabilité de tirer zéro dossier correspondant à une personne sans expérience professionnelle.
1-0,83 = 0,488.
Une
étude a montré que le temps d'attente, exprimé en nombre de semaines,
pour qu'un candidat passe un entretien avec le service des ressources
humaines est une variable aléatoire réelle X qui prend des valeurs
entières non nulles et vérifie :
Pour tout entier k >0, on a : P(X=k) = 2k-1 / 3k.
3. Démontrer par le calcul la relation suivante.
Pour k = 1 à plus l'infini, SP(X=k)=1.
On définit la suite (Un) par un = (2 / 3)k-1 x 1 / 3.
Il s'agit d'une suite géométrique de raison 2 / 3 et de premier terme 1 / 3.
La somme des termes de cette suite vaut : 1 / 3 [ 1-(2/3)k] / (1 /3)= 1-(2/3)k.
0 < 2 / 3 < 1, alors (2/3)k-1tend vers zéro si k tend vers plus l'infini.
4. Quelle est la probabilité qu'un candidat attende 3 semaines avant de passer son entretien ?
P(X=3) = 23-1 / 33=4 /27 ~0,15.
5.a. Quelle est la probabilité qu'un candidat attende au moins 4 semaines ?
P(X > 4)=1-P(X=1)-P(X=2)-P(X=3) = 1-21-1 / 31 - 22-1 / 32 - 23-1 / 33=1- 1 / 3 -2 / 9 - 4 / 27.
P(X > 4)=27 / 27 -9 / 27 -6 / 27 -4/27 = 8 /27 ~0,30.
5.b. Quelle est la probabilité qu'un candidat attende au moins k semaines ?
P(X > k)=1- (1-(2/3)k)= (2/3)k.
|
|