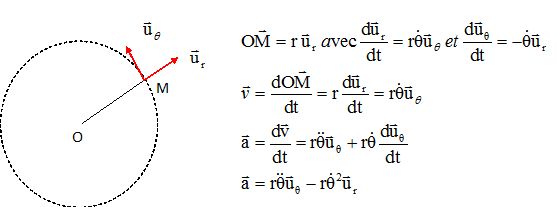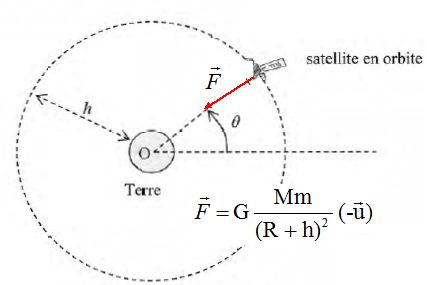
Physique, concours externe TSPEI 2016. Technicien Supérieur Principal de l'Economie et de l'Industrie En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Satellite d'observation. Un satellite de masse m = 700 kg est en mouvement circulaire, autour de la terre, à une altitude h. On suppose la terre sphérique de rayon R et de masse M. On repère le satellite par la distance r par rapport au centre de la terre et q, l'angle entre OS et une direction fixe du plan de la trajectoire. 1.1 Ecrire le vecteur accélération du satellite, considéré comme une masse ponctuelle, dans  la base polaire en fonction de r, q et des dérivées temporelles de q. 1.2a. En appliquant la deuxième loi de Newton au satellite, montrer que la vitesse angulaire du satellite est constante. 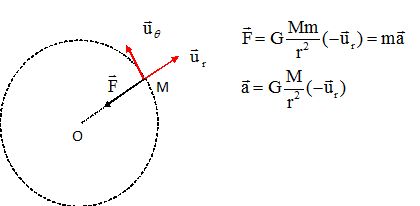Par suite GM / r2 = r q'2 et q" = 0 soit q' = constante. 1.2b. Déterminer l'expression de la norme v de la vitesse du satellite. GM / r2 = r q'2 avec v = rq' ; v2 = GM / r ; v = [GM / r]½. 1.3a. Exprimer la période T du satellite en fonction de G, M R et h. La troisième loi de Kepler s'écrit : T2 / (R+h)3 = 4 p2 / (GM) ; T = [4 p2(R+h)3 / (GM) ]½. 1.3b Qu'appelle t-on satellite géostationnaire ? Déterminer la valeur numérique de l'altitude h d'un tel satellite. Le satellite géostationnaire tourne dans le plan équatorial, dans le même sens que la Terre, avec la même vitesse angulaire que la Terre. M = 5,98 1024 kg ; R = 6,38 103 km ; période de rotation de la terre : T = 23 h 56 min 4 s. T =23x3600 +56 x60 + 4 = 86164 s. (R+h)3=861642 x6,67 10-11 x5,98 1024 / (4 x3,142) =7,508 1022 ; R+h = 4,22 107 m = 4,22 104 km. h = 4,22 104 -6,38 103 ~3,6 104 km. 1.3c. En raison d'un problème, le satellite n'a pas été placé sur l'orbite circulaire visée. Il se trouve sur une orbite elliptique de 25900km d'apogée et 13700 km de périgée. Déterminer la période de révolution du satellite. Demi-grand axe de l'ellipse : a = (25900 + 13700) / 2 = 1,98 104 km = 1,98 107 m. T2 / a3 = 4 p2 / (GM) ; T = [4 p2a3 / (GM) ]½. T = [4 x3,142 x(1,98 107)3 /(6,67 10-11 x5,98 1024)]½ =2,77 104 s. Régulation de température. Un syqtème de régulation permet de mettre en fonctionnement une climatisation selon les besoins. La capteur de température est une résustance de type CTN dont la résistance R est de la forme R(T) = R0 exp(a / T) où T est la température en Kelvin. 2.1a. Quand on passe de T1 = 273 K à T2 = 323 K la résistance varie de R1 = 5000 ohms à R2 = 100 ohms. Calculer R0 et a. 5000 =R0 exp(a / 273) ; 100 =R~ exp(a / 323) ; 5000 / 100 = 50 = exp((1 /273-1 /323) a) = exp(5,67 10-4 a) ; ln 50 = 5,67 10-4a ; a =6899~ 6,9 103 K. R0 = 100 / exp( 6899 / 323) ~ 5,2947 10-8 ~5,29 10-8 ohms.   2.1b. Calculer R pour T = 293 K. R = 5,2947 10-8 exp(6,89 103 / 293) ~891 ohms. 2.2. Un relais (K) commande la climatisation. La résistance propre du relais est RK = 100 ohms. La plage d'enclenchement du relais est comprise entre 1,5 V et 3,0 V. Cela signifie que : - si la tension UK aux bornes du relais est  inférieure à 1,5 V, le relais est ouvert et la climatisation est arrêtée ; - si la tension UK aux bornes du relais est supérieure à 3,0 V, le relais est fermé et la climatisation fonctionne ; - entre 1,5 V et 3,0 V la fermeture peut se produire de façon aléatoire. On envisage le montage suivant où la résistance R(T) est à la température du local. 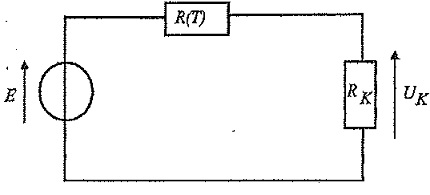2.2a. Comment appelle t-on ce type de montage ?. Montage en série, diviseur de tension. 2.2b. Exprimer UK en fonction de E et des résistances. UK = RK I ; E = (R(T) +RK) I  ; UK =  RK E / (R(T) +RK). 2.2c. Calculer E pour que UK = 2,25 V lorsque T = 293 K. Expliquer le choix de 2,25 V. 2,25 = (1,5 +3) / 2 , valeur moyenne de la plage d'enclenchement.. 2,25 = 100 E / (891 +100) ; E = 22,3 V. 2.2d. Calculer les températures T(1,5 V) et T(3,0 V). Commenter. 1,5 = 22,3 x100 / (R(T) +100) ; R(T) +100 = 2230 / 1,5 = 1487 ; R(T) = 1387 ohms. 1387 = 5,2947 10-8 exp(6,899 103 / T)  ; ln(2,62 1010) = 6,899 103 / T ; T = 287,6 K soit 14,6°C. 3,0 = 22,3 x100 / (R(T) +100) ; R(T) +100 = 2230 / 3 = 743,3 ; R(T) =643,3 ohms. 643,3 = 5,2947 10-8 exp(6,899 103 / T)  ; ln(1,215 1010) = 6,899 103 / T ; T = 297 K soit 24°C. La climatisation est arrêtée quand la température est inférieure à 14,6°C et elle fonctionne dès que la température dépasse 24 °C. Fission et fusion. Dans une centrale nucléaire, une des réactions de fission les plus courantes s'écrit : 23592 U +10n ---> 9438Sr + 140ZXe + x10n. 3.1.1. Déterminer Z et x en justifiant. Conservation de la charge : 92 =38 +Z soit Z = 54. Conservation du nombre de nucléons : 235 +1 = 94 +140 +x soit x = 2. 3.1.2. Déterminer la variation de masse Dm. Dm = m(9438Sr) +m(140ZXe) +m(10n) -m(23592 U) =93,8945+139,892+1,00866-234,9935= -0,19834 u. -0,19834 x1,66054 10-27 = -3,2935 10-28 kg. 3.1.3. Enoncer la relation d'équivalent masse-énergie. E = Dm c2. 3.1.4. En déduire l'énergie libére ( J et eV) par la fission d'un noyau d'uranium. -3,2935 10-28 x(3 108)2= -2,964 10-11 J soit -3,2935 10-28 / (1,6 10-19)= -1,85 108 eV. 3.1.5. L'uranium 238 peut par capture d'un neutron rapide, donner l'isotope 23992U. Ce dernier est radioactif et par suite d'émissions successives de particules X, se transforme en plutonium 23994Pu. Identifier X. 23992U  ---> 23994Pu +2 0-1e (électron). On considère la réaction de fusion : 21H +31H ---> 42He +10n. 3.2.1. Déterminer l'énergie libérée par cette fusion. Dm = m(42He) +m(10n) -m(31H) -m(21H) = 4,0015+1,00866-2,0136-3,0155= -1,894 10-2 u. 1,894 10-2 x1,66054 10-27 = -3,145 10-29 kg. -3,145 10-29 x(3 108)2= -2,83 10-12J. 3.2.2a Un litre d'eau de mer contient m = 30 mg de deutérium. Déterminer l'énergie libérée par V = 3,0 litres d'eau de mer et l'exprimer en Tonne Equivalent Pétrole. Nombre de noyaux de deutérium dans 3 L d'eau de mer : 90 mg = 9 10-5 kg. 9 10-5 /(2,0136 x1,66054 10-27) =2,69 1022. E = 2,83 10-12 x2,69 1022 = 7,61 1010 J. 1 TEP = 40,5 109 J. 7,61 1010 / (40,5 109) ~1,9 TEP. Découpe d'une feuille d'aluminium. Une feuille d'aluminium horizontale, d'épaisseur e = 0,50 mm reçoit perpendiculairement à sa surface, un faisceau laser de section circulaire S = 0,20 mm2 et de puissance P = 4,0 W. La température initiale de la feuille est T0 = 290 K et on opère sous la pression atmosphérique normale. 4.1. Exprimer l'énergie E émise par ce laser durant la durée Dt. E = P Dt. 4.2 Exprimer la masse d'aluminium m recevant l'énergie du laser. m = S e rAl = 2,0 10-7 x 5 10-4 x2700=2,7 10-7 kg. 4.3a. Exprimer l'énergie Q1 qu'il faut apporter à la masse m pour la faire passer de la température T0 à la température de fusion sans changer d'état. Q1 = m Cal(Tfusion -T0) = m x 900 (933-290 )=5,787 105 m joules 4.3b Exprimer l'énergie Q2 qu'il faut apporter à la masse m pour la faire fondre entièrement la température restant constante égale à Tfusion. Q2 = m Lfusion = 3,93 105 m joules. 4.3c. On suppose que toute l'énergie du laser est absorbée par le métal. Quelle est l'expression de la durée minimale t pendant laquelle il est nécessaire d'illuminer l'aluminium pour réchauffer puis faire fondre entièrement la zone ? P t = Q1 + Q2 = m Cal(Tfusion -T0) +m Lfusion ; t =[ m Cal(Tfusion -T0) +m Lfusion ] / P.

menu