Mathématiques, concours externe TSPEI 2015. Technicien Supérieur Principal de l'Economie et de l'Industrie En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Premier problème. On considère la fonction f définie sur ]0 ; +oo[ par : f(x) = ln( x / (x+1)) + 1 / x. 1. Calculer f(1/3) et f(1/2) en fonction de ln2 et ln3.   f(1/3) = ln(1/3 / (4/3)) +3 = ln(1/4) +3 = -ln(22)+3 = -2 ln2 +3.   f(1/2) = ln(1/2 / (3/2)) +2 = ln(1/3) +2 = -ln(3)+2. 2. Déterminer la limite de f(x) quand x tend vers 0+. Interpréter graphiquement cette limite. On rappelle que si x tend vers 0+ alors x ln x tend vers zéro. f(x) =[ x ln(x / (1+x) +1] / x. Quand x tend vers 0+, 1 +/ x tend vers 1 ; ln(x / (1+x) tend vers ln (x) et x ln(x) tend vers zéro. f(x) est équivalent à 1 / x; f(x) tend vers plus l'infini. L'axe vertical est asymptote à la courbe C représentant f(x). 3. Déterminer la limite de f(x) quand x tend vers plus l'infini. Interpréter graphiquement cette limite. Quand x tend vers plus l'infini : 1 / x tend vers zéro. x / (1+x) = 1 /(1 /x+1) tend vers 1 et ln(x /(1+x)) tend ver zéro. f(x) tend vers zéro et l'axe des abscisses est asymptote à la courbe C. 4. Calculer la dérivée de f(x) et en déduire le tableau de variation. On pose u = x et v = 1+x ; u' = 1 et v' = 1 ; (u'v -v'u) / v2 =(1+x -x) / (1+x)2. f '(x) = 1 /(x(1+x)) -1/x2 =1 / x [ 1 /(1+x)-1 / x]= -1 /(x2(1+x)). f '(x) est strictement négative et f(x) est strictement décroissante sur ]0 ; +oo[. 5. Montrer que l'équation f(x) = 1 possède une unique solution notée a et que 1 / 3 < a <1 / 2. 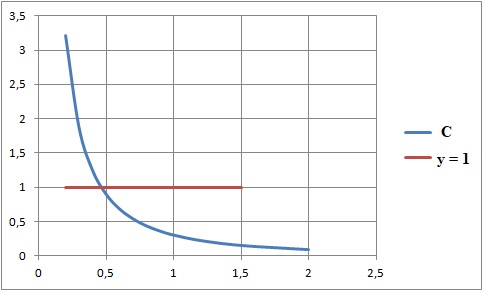f(1/3) = 3-2ln 2 ~1,6 supérieur à 1 ; f(1/2) = 2-ln(3) ~0,9, inférieur à 1. f(x) est strictement décroissante. D'après le théorème des gendarmes l'équation f(x) = 1 possède une unique solution notée a et que 1 / 3 < a <1 / 2. Soit la fonction g définie sur l'intervalle ]0 ; +oo[ par : g(x) = 0,5 x f(x) +0,5 x. 6. Calculer g'(x). Montrer que pour tout x appartenant à [1 /3 ; 1 /2 ] on a |g'(x)| < 0 ,4. Dérivée d'un produit 0,5 x f(x) :  0,5 f(x) +0,5x f '(x)=0,5 [ ln( x / (x+1)) + 1 / x - 1 / (x(1+x))] = 0,5 [ ln( x / (x+1)) + 1 / (1+x)] . g'(x) =0,5 [ ln( x / (x+1)) + 1 / (1+x) +1] . g"(x) = 0,5 [1 /(x(1+x))-1/(1+x)2]= 0,5 /(x(1+x)2). g"(x) est strictement positive sur ]0 ; +oo[ ; g'(x) est strictement croissante sur cet intervalle. 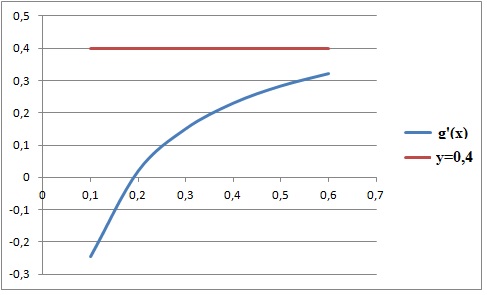g'(1/3)=0,5[-2ln(2)+1,75] = -ln2 +0,875 < 0,4. g'(1/2) =0,5[ -ln(3) + 5 /3 ] < 0,4. 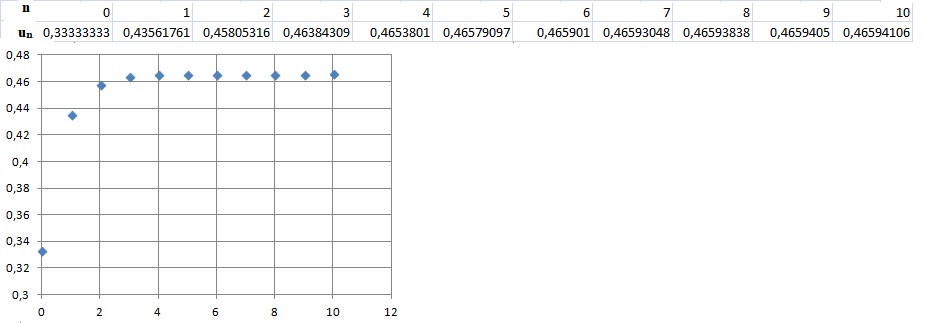g'(x) est strictement croissante : |g'(x)| < 0 ,4 pour tout x appartenant à [1 /3 ; 1 /2 7. Soit la suite (un) définie par, pour tout n entier naturel : u0 = 1 /3 ; un+1 = g(un) pour n entier naturel non nul. Montrer que cette suite est convergente et donner sa limite. On admettra que 0,6 < ln(2) < 0,7 et que 1 < ln(3) < 1,1. g(x) = 0,5 x (  f(x) +1) = 0,5 x (ln( x / (x+1)) + 1 / x +1)= 0,5 x (ln( x / (x+1)) + (x+1) / x). g'(x) est positive sur [1 /3 ; +oo[ : g(x) est strictement croissante sur cet intervalle. un+1-un = g(un)-g(un-1) >0. La suite est croissante. u1 =g(u0) =0,5u0 [ln(u0/(1+u0)+(u0+1)/u0]. u1 = g(1/3)=(4-2ln2) / 6. u1 est compris entre  (4-2x0,6) / 6 et(4-2x0,7) / 6 soit entre 0,466 et 0,433. La suite étant croissante et bornée, elle est convergente. Second problème. Une urne contient initialement une boule blanche et une boule rouge. On effectue des tirages successifs d'une boule dans l'urne selon le protocole suivant :  après chaque tirage, la boule tirée est remise dans l'urne, et l'on ajoute dans l'urne, avant le tirage suivant, une boule de la même couleur que celle qui vient d'être tirée. Les tirages sont équiprobables. Pour i entier naturel non nul, on introduit les événements suivants : Bi : on obtient une boule blanche lors du i-ème tirage. Ri : on obtient une boule rouge lors du i-ème tirage. 1.Quelle est la probabilité d'obtenir une boule blanche au premier tirage ? P(B1 )= 0,5. 2. Quelle est la probabilité d'obtenir une boule blanche au second tirage ? 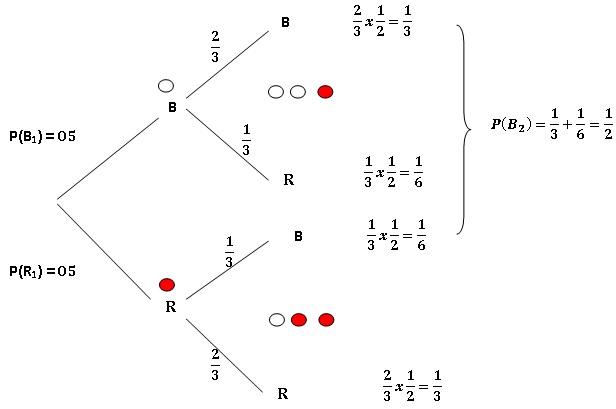3. Si la deuxième boule est blanche, quelle est la probabilité que la première boule tirée ait été blanche ? (1 / 3 ) / (1/ 2) = 2 / 3. Pour tout entier naturel non nul, on note Xn la variable aléatoire égale au nombre de boules blanches obtenues au cours des n premiers tirages. 4. Déterminer P(X2 =0), P(X2 = 1) et P(X2 = 2). P(X2 =0) =1 / 3. P(X2 = 1)=1 / 6 +1 / 6 = 1 / 3. P(X2 = 2)=1 / 3. 5. Calculer l'espérance mathématique de X2. Interpréter le résultat obtenu. 0 x P(X2 =0)+ 1 x P(X2 = 1) + 2 x P(X2 = 2) = 1 / 3 + 2 / 3 = 1. Au bout de deux tirages, on obtient en moyenne une boule blanche. 6. A l'aide des questions précédentes, calculer P(X3 = k) avec k = 0, 1, 2 et 3. 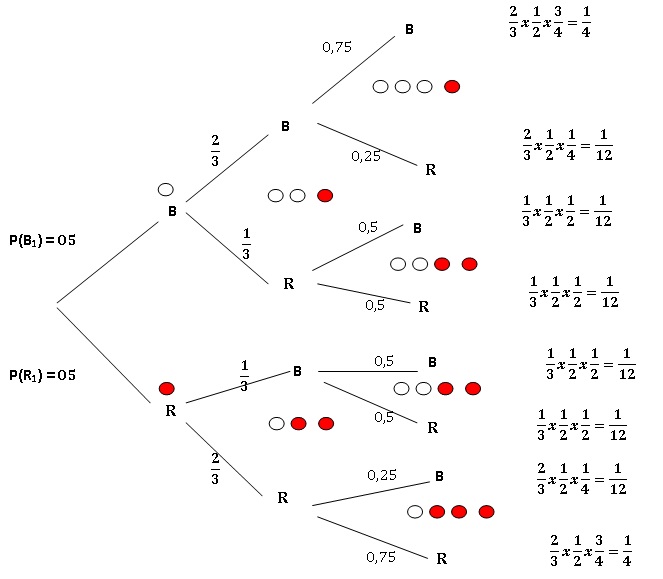P(X3 =0) =1 / 4. P(X3 = 1)=3 / 12=1 / 4. P(X3 = 2)=3 / 12 = 1 /4. P(X3 = 3)=1 / 4. 7. Soit n un entier naturel non nul. Déterminer, pour tout entier naturel k tel que 0 < k < n, P(Xn = k). P(Xn = k) = 1 / (n+1).

menu