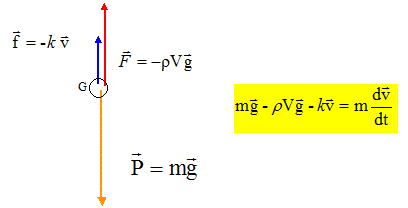Physique,
concours externe TSPEI 2015.
Technicien Supérieur Principal de l'Economie et de l'Industrie
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Fibre optique.
A Phénomène de réflexion totale.
A.1. Que signifie le terme "lumière monochromatique " en optique.
La lumière émise par la source possède une unique fréquence, donc une seule couleur.
Par la suite, les rayons lumineux sont tous supposés issus d'une radiation monochromatique.
On considère un rayon lumineux arrivant sur l'interface plane séparant
deux milieux d'indices différents sous un angle d'incidence i.
A.2 A l'aide d'un schéma clair, énoncer les lois de Descartes pour la réflexion et la réfraction.
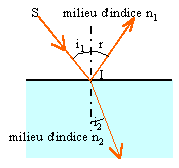
Rayons incident, réfléchi et réfractés sont coplanaires.
L'angle d'incidence et l'angle de réfléxion ont la même mesure : i = r.
Loi concernant la réfraction : n1 sin i1 = n2 sin i2.
A.3. On suppose que n1 > n2. Montrer qu'il existe un angle limite d'incidence iL tel que si i > iL, aucun rayon réfracté ne peut émerger et que le rayon incident est entièrement réfléchi.
n1 sin i1 = n2 sin i2 avec |sin i | < 1.
sin i1 =n2 / n1 sin i2 .
La plus grande valeur possible de l'angle réfraction est i2 = 90 ° ; alors sin iL = n2 / n1.
B. Fibre à saut d'indice.
 B.1
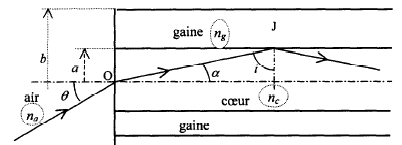
A quelle condition sur i, angle d'incidence à l'interface coeur/gaine,
le rayon rest-t-il confiné à l'intérieur du coeur de la fibre ? Faire
apparaître plusieurs réflexions à l'intérieur de la fibre.
B.1
A quelle condition sur i, angle d'incidence à l'interface coeur/gaine,
le rayon rest-t-il confiné à l'intérieur du coeur de la fibre ? Faire
apparaître plusieurs réflexions à l'intérieur de la fibre.
En J, on doit avoir une réflexion totale.
L'angle d'incidence limite en J est tel que sin iL = ng / nc avec n c > ng. L'angle d'incidence i doit être supérieur à iL.
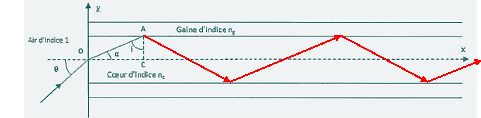
B.2. Montrer que la condition précédente est vérifiée si l'angle d'incidence q est inférieur à un angle limite qL tel que sin qL = nc cos iL. En déduire lexpression de l'ouverture numérique O.N = sin qL en fonction de nc et ng uniquement.
a + i = 90° ; i > iL, donc a < 90-iL.
Il y a toujours réfraction en O, car nc > nair. Réfraction en O : nair sin q = nc sin a.
sin q = nc sin a = nc sin (90-i)= nccos ( i).
Dans le cas limite de la réflexion totale en J : sin qL = nc cos iL.
Il y a réflexion totale en J si q < qL.
ON =sin qL =nc cos iL.
De plus sin iL = ng/ nc.
cos2iL = 1-sin2iL =1-(ng/ nc)2.
ON = nc[1-(ng/ nc)2]½ = [nc2-ng2]½.
B.3.nc = 1,500 et ng = 1,470. Calculer O.N.
ON=(1,502-1,472)½=0,298.
On considère une fibre optique de longueur L. Le rayon entre dans la fibre avec un angle d'incidence q variable compris entre 0 et qL.
B.4. Donner la relation liant la célérité de la lumière v dans le coeur de la fibre et la célérité de la lumière dans le vide.
v = c / ng.
B.5. Quel est le rayon qui traverse le plus rapidement la fibre ? Calculer la durée du parcours t1 de ce rayon en fonction de L, c et nc.
Il s'agit du rayon traversant la fibre selon son axe. (q = 0). t1 =L / v = Lnc /c.
B.6. Quel est le rayon qui met le plus de temps pour traverser la fibre ? Calculer la durée du parcours t2 de ce rayon en fonction de L, c, nc et sin iL.
Il s'agit du rayon arrivant sous incidence qL. Il parcourt la distance L / sin iL.
t2 =L /( v sin iL)= Lnc /( c sin iL) avec sin iL = ng / nc ; t2 =Ln2c /( c ng).
B.7. En déduire l'intervalle de temps dt entre le temps de parcours minimal et maximal en fonction de L, c, nc et ng.
dt =Ln2c /( c ng)- Lnc /c= Lnc / c (nc / ng-1).
B.9. On pose 2D = 1-(ng/nc)2. Montrer que si D << 1, dt ~L / c nc D.
(ng/nc)2 = 1-2D ; ng/nc = (1-2D)½ ; nc / ng =(1-2D)-½ ~1+D.
nc / ng-1~D et dt ~L / c nc D.
|
|
|
|
Moteur Stirling.
On étudie un moteur idéal au cours duquel, n mol de gaz parfait de rapport g = Cp / Cv subissent les évolutions suivantes :
- compression 1 ---> 2 isotherme réversible à la température T1 = 300 K.
- échauffement 2 ---> 3 isochore jusqu'à l'état 3 de température T3 = 600 K.
- détente 3 ---> 4 isotherme réversible à la température T3.
- refroidissement 4 ---> 1 isochore jusqu'à l'état 1.
Il n'y a pas de travail autre que celui des forces de pression. On rappelle que Cv = nR /(g-1).
1. représenter l'allure du cycle dans un diagramme (P, V) Le cycle est-il moteur ou récepteur ?
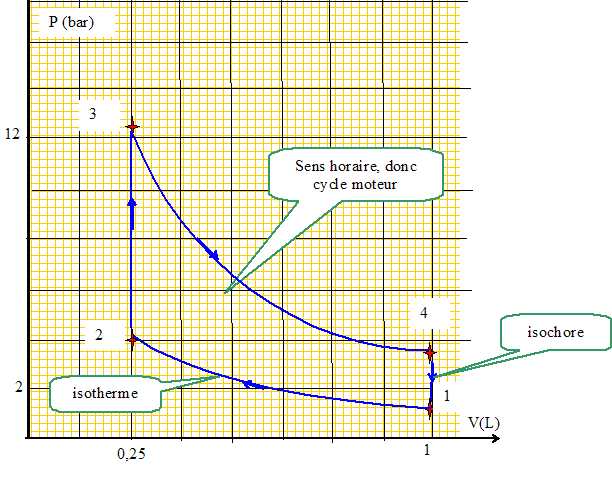
2. Exprimer le travail W12 reçu par le fluide au cours de la compression en fonction de n, R, T1 et du rapport de compression r = V1 / V2. En déduire le transfert thermique Q12 reçu par le fluide au cours de cette compression en fonction de n, R, T1 et r. Préciser les signes de W12 et Q12.
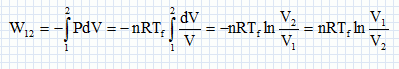 W12 = nRT1 ln r >0. W12 = nRT1 ln r >0.
L'énergie
interne d'un gaz parfait ne dépend que de la température. Au cours d'une
transformation isotherme, l'énergie interne du gaz parfait ne varie pas.
DU12 = 0 ; DU12 =W12 +Q12 d'où Q12 = -W12 ; Q12 < 0.
3. Exprimer le transfert thermique Q23 reçu par le fluide au cours de l'échauffement en fonction de n, R, T1, T3 et g. Préciser son signe.
Le travail est nul au cours d'une transformation isochore.
DU23 =W23 +Q23 =Q23 =n Cvm ( T3-T1) = nR /(g-1) ( T3-T1) >0.
4. Exprimer le trravail reçu par le fluide au cours de la détente W34 en fonction de n, R, T3 et r. En déduire le transfert thermique Q34 reçu par le fluide au cours de cette compression en fonction de n, R, T3 et r. Préciser les signes de W34 et Q34.
W34 = nRT3 ln(V3 / V4) = nRT3 ln(V2 / V1) = -nRT3 ln r <0.
L'énergie
interne d'un gaz parfait ne dépend que de la température. Au cours d'une
transformation isotherme, l'énergie interne du gaz parfait ne varie pas.
DU34 = 0 ; DU34 =W34 +Q32 d'où Q34 = -W34 ; Q34 > 0.
5. Exprimer le transfert thermique Q41reçu par le fluide au cours du refroidissement en fonction de n, R, T1, T3 et g. Préciser son signe.
Le travail est nul au cours d'une transformation isochore.
DU41 =W41 +Q41 =Q41 =n Cvm ( T1-T3) = nR /(g-1) ( T1-T3) < 0.
6. Le régénarateur étant idéal, on a Q23 +D41
= 0. Quelle est alors, sur le plan énergétique, la grandeur coûteuse
pour l'utilisateur de ce système sur un cycle ? La grandeur énergétique
utile est le travail fourni par le fluide sur le cycle. En déduire
l'expression du rendement en fonction de T1 et T3. Commenter et faire l' application numérique.
La compression isotherme est la grandeur coûteuse.
h = |W34 + W12| / Q34 =(T3-T1) / T3.
h =1-T1 / T3 = 1-300 / 600 = 0,5 ( 50 %).
Le
cycle de Carnot est un cas idéal dans lequel toutes les transformations
sont réversibles. Il indique quel est le rendement maximal possible. Les transformations réelles ne sont pas réversibles.
Dans
la réalité, l'hypothèse faite " récupérer totalement la quantité
d'énergie échangée par chaleur lors du refroidissement
isochore pour la restituer au cours du chauffage isochore", est en
réalité impossible à réaliser sur le plan pratique. Il faudrait
pour cela que le régénérateur ait une efficacité de 100 %.
|
|
|
|
|
Chute d'un bloc de CO2.
Une proposition volontairement simpliste consisterait à former des blocs de CO2
solide à l'aide d'une installation frigorifique puis de les
laisser tomber dans les fosses marines. On effectue les approximations
suivantes :
L'océan est un fluide homogène au repos, de température constante, incompressible et indilatable.
Les blocs de CO2 sont incompressibles et indilatables. Ils ont une masse constante tout au long de la descente.
Masse volumique de l'océan r = 1,03 103 kg m-3 ; du bloc de CO2 : rbloc = 1,50 103 kg m-3 ; g =9,80 m s-2.
Le repère est orienté suivant la verticale descendante.
Un bloc de CO2 solide de volume V = 650 m3 est
lâché à la surface de l'océan à l'instant t = 0. Lors de sa descsnte,
il subit, entre autres, une force de frottement fluide proportionnelle
à la vitesse f = k v avec k = 8,0 104 kg s-1.
1. Faire un bilan complet des forces appliquées au solide.
Le solide est soumis à son poids, à la poussée d'Archimède et à la force de frottement fluide.
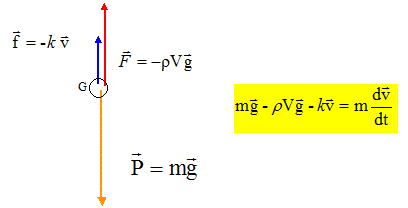
2. Enoncer la relation fondamentale de la dynamique..
Dans un référentiel galiléen, la
somme vectorielle des forces extérieures
appliquées au système est égale au
produit de la masse du solide par
l'accélération de son centre d'inertie G.
3. Etablir l'équation différentielle vérifiée par la vitesse.
Projeter la seconde loi de Newton selon un axe vertical orienté vers le bas.
mg -rVg-kv =mdv/dt.
dv /dt +k / m v = g(1-Vp / m) avec m = V rbloc .
4. Donner l'expression puis calculer la vitesse limite du solide.
dvlimite / dt = 0 ; mg -rVg-kvlimite =0 ; vlimite =g (m -rV ) / k = 9,8(650 x 1,5 103-650x1,03 103) /(8,0 104) =37,42 ~37 m /s.
5. Donner l'expression de la vitesse v(t) du bloc en fonction de vlimite et d'une constante homogène à un temps t = rbloc V / k.
dv /dt +k / (V rbloc) v = g(1-p / rbloc) avec vlimite =gV (rbloc -r ) / k.
dv/dt +v / t =g(1-p / rbloc). (1).
Solution générale de dv/dt +v / t =0 : v(t) = A exp (-t / t) avec A une constante.
Solution particulière de (1) : v(t) = vlimite.
Solution générale de (1) : v(t) =A exp (-t / t)+ vlimite.
v(t=0) = 0 d'où A = -vlimite.
v(t) = vlimite(1-exp (-t / t)).
6. En déduire l'expression de la profondeur z(t) du bloc.
z(t) est une primitive de v(t).
z(t) = vlimite(t+ t exp (-t / t))+ constante.
z(t=0) = 0 = vlimite(0+ t )+ constante ; constante = -vlimite t.
7. Commenter en quelques lignes cette proposition de
limitation de rejet de dioxyde de carbone. Citer une autre proposition
pour limiter ces rejets.
La température et la masse volumique de l'océan dépend de la profondeur. Il y a en plus les courants marins.
Des
recherches sont menées pour piéger le dioxyde de carbone émis dans des
solides poreux, comme certains oxydes métalliques tels que la cérine ou
oxyde de cérium CeO2, qui sert actuellement comme capteur de gaz.
L'hydrogénation du CO2 (
réaction avec le dihydrogène et production d'eau dite réaction de
Sabatier ) est la voie de conversion la plus étudiée. Elle peut
conduire directement à la formation d'alcools, d'hydrocarbures... C'est
ainsi que les synthèse du méthanol, de l'éthanal CH3-CH sont souvent envisagées, de même que la réaction qui mêne au méthane.
|
|
Modélisation électrique d'un câble coaxial.
Le câble coaxial peut être modélisé par un circuit A1A2, constitué d'une chaîne de n modules identiques comportant chacun trois résistors. Un dipôle résistor X1X2 de résistance 2R est branché en parallèle à l'extrémité de la chaîne.
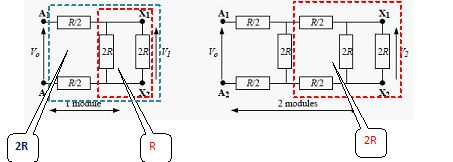
1.1. Le dipôle A1A2 est équivalent à un résistor.
Rappeler les lois d'association de résistances branchées en série et en parallèle.
Les résistances en série s'ajoutent.
En dérivation, les conductances ( inverse des résistances) s'ajoutent.
1.2 .Exprimer,
en fonction de R, la résistance équivalente R1 dans le cas d'une
chaîne comportant un seul module.
Deux résistances identiques de valeur 2R sont en dérivation :
résistance équivalente R.
Trois résistances de valeur, ½R, ½R, R sont en série : R1
= ½R+½R+R = 2R.
1.3. Même
question pour une chaîne à 2 modules, puis à n modules.
La résistance équivalente du second module vaut 2R.
Deux
résistances identiques de valeur 2R sont en dérivation : résistance
équivalente R.
Trois résistances de valeur, ½R, ½R, R sont en série : R2
= ½R+½R+R = 2R.
Chaîne à n modules
: hypothèse Rn = 2R. Calculons Rn+1 :
Deux
résistances identiques de valeur 2R sont en dérivation : résistance
équivalente R.
Trois
résistances de valeur, ½R, ½R, R sont en série : Rn+1
= ½R+½R+R = 2R.
Le dipôle A1A2 est alimenté par un générateur de
tension constante V0 = VA1-VA2.
2.1.a. Un dipôle AB
est constitué de deux résistors. Les deux résistors sont montés en
série et l'ensemble est soumis à une tension u. Exprimer u2, tension aux bornes du résistor R2, en fonction de u, R1, R2.
Soit i l'intensité traversant les deux résistors.
u = (R1+R2)i et u2 = R2i =R2 u / (R1+R2).
2.1.b. Les deux résistors sont montés en parallèle et l'ensemble est soumis à une tension u. Exprimer i2, intensité du courant dans le résistor R2, en fonction de i ( intensité dans le dipôle AB), R1, R2.
u = R1 i1 = R2 i2 et i = i1 + i2 ; i2 = R1 i1 / R2 = R1 ( i-i2) / R2 ;
i2R2 +R1i2 = R1 i ; i2 = R1 i / (R1+R2).
2.2. Déterminer
en fonction de V0,et R, la tension V1 =VX1-VX2 aux bornes du
résistor X1X2 dans le cas d'une
chaîne à 1 module.
I = V0 / R1 = V0/(2R) ; V1
= R I = ½V0.
2.3. Même
question pour une chaîne à 2 modules puis à n modules.
I = V0 / (2R) ; V1 =½V0 ; V2 =½V1 = V0/4 = V0 / 22.
Chaîne à n modules :
hypothèse Vn = V0/2n. Calculons Vn+1
:
Vn+1 =Vn / 2 = ½ V0/2n
= V0 / 2n+1.
En
déduire la valeur de Vinfini pour une chaîne de
longueur infinie.
Vinfini tend vers zéro si n tend vers l'infini.
|
|




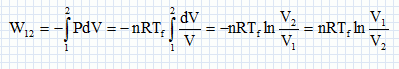 W12 = nRT1
W12 = nRT1