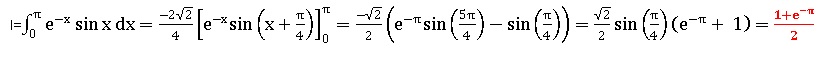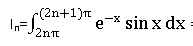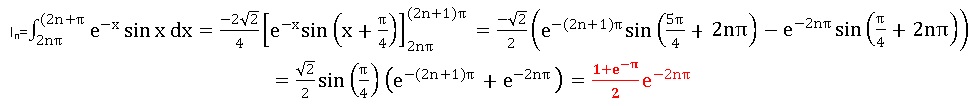Mathématiques,
concours externe TSPEI 2014.
Technicien Supérieur Principal de l'Economie et de l'Industrie
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Premier problème.
1. Montrer que pour tout réel x on a : cos x - sin x = 2½ cos ( x+p/4).
cos ( x+p/4) = cos x cos (p/4) - sinx sin (p/4) )= 2½ / 2 cos x - 2½ / 2 sin x.
2 / 2½ cos ( x+p/4) = cos x - sin x.
2½ cos ( x+p/4) = cos x - sin x.
2. Résoudre dans l'intervalle [-p/2 ; p ], l'équation cos (x +p/4) = 0.
x+p/4 = ±p/2 + 2kp.
x = ±p/2 -p/4+ 2kp.
Si k =0 : x = p/4.
On considère la fonction définie sur l'intervalle [-p/2 ; p ] par :
f(x) =e-x sin x.
3.Calculer f(-p/2), f(0), f(p/4) et f(p).
f(-p/2) = -exp(p/2) ; f(0) = 0 ; f(p/4)=2½ / 2 exp(-p/4) ; f(p) = 0..
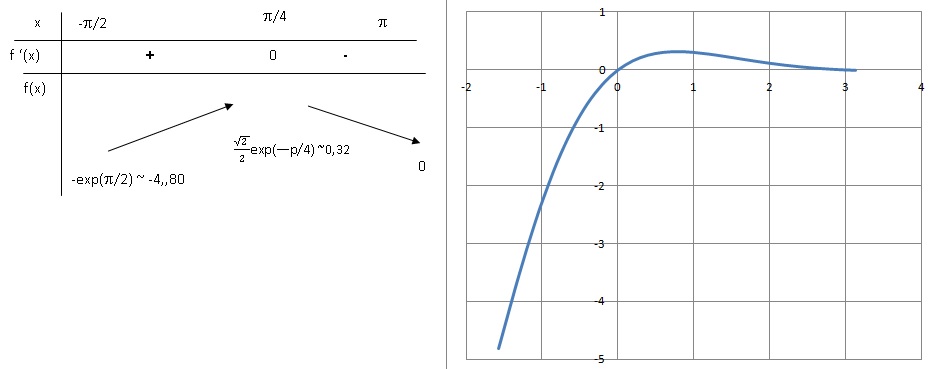
4. Calculer la dérivée de f(x) et en
déduire le tableau de variation.
On pose u = e-x et v = sin x ; u' = - e-x et v' = cos x ; u'v +v'u= - e-xsin x+cos x e-x = e-x( cos x -sin x) =2½ e-x cos( x +p/4).
e-x est toujours positif ; f '(x) a le signe de cos( x +p/4).
f '(x) s'annule pour x = p/4.
f '(x) est négative sur [ p/4 ; p], la fonction f (x) est strictement décroissante sur [ p/4 ; p].
f '(x) est positive sur [ -p/2 ; p/4], la fonction f (x) est strictement croissante sur [ -p/2 ; p/4].
f(x) présente un maximum pour x = p/4.
5. Calculer les dérivées successives de la fonction f jusqu'à l'ordre 4 notée f(4). Trouver une relation entre f et f(4).
On pose u =2½ e-x et v = cos( x +p/4) ; u' = -2½ e-x et v' = -sin( x +p/4) ; u'v +v'u= - 2½e-xcos( x +p/4)-2½sin( x +p/4) e-x .
f(2)= -2½e-x( cos( x +p/4)+sin( x +p/4)).
On pose u = -2½e-x et v = cos( x +p/4)+sin( x +p/4) ; u' = 2½ e-x et v' = -sin( x +p/4) +cos( x +p/4).
u'v +v'u= 2½e-x(cos( x +p/4)+sin( x +p/4))-2½e-x(cos( x +p/4)-sin( x +p/4)).
f(3)= 2*2½e-xsin( x +p/4).
On pose u = 2*2½e-x et v = sin( x +p/4) ; u' = -2*2½e-x et v' = cos( x +p/4).
u'v +v'u= -2*2½e-xsin( x +p/4)+2*2½e-xcos( x +p/4).
f(4)= 2*2½e-x(cos( x +p/4)-sin( x +p/4)).
On pose X = x +p/4 ; (cos( x +p/4)-sin( x +p/4)) =2½cos (X+p/4) = 2½cos (x+p/2) = -2½sin x.
f(4)= -4e-xsin x = -4f(x). f(3) est une primitive de f(x).
6. Calculer l'intégrale suivante.
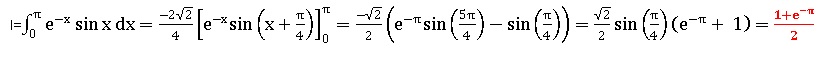
|
|
|
|
7. Pour tout entier naturel n, on pose :
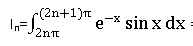
a. Déterminer I0.
I0=0,5(e-p +1)
b. Pour tout entier n calculer In.
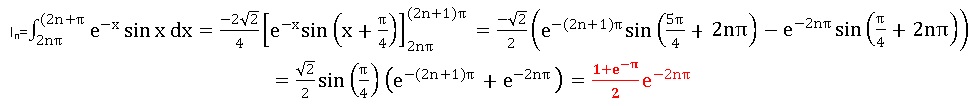
c. Montrer que la suite (In) , n entier naturel, est géométrique.
In = I0 exp(-2np).
Cette suite est géométrique de premier terme I0 et de raison exp(-2p).
d. Cette suite est-elle convergente ?
In+1 -In = I0 (exp((-2n+1)p) -exp((-2n)p)= I0 exp((-2n)p) (exp(-p)-1) <0.
La suite est décroissante.
Quand n tend vers plus l'infini, In tend vers zéro. la suite est bornée.
La
suite étant décroissante et bornée, elle est convergente.
|
|
|
|
|
Second
problème.
On dispose d'un lot de 100 pièces de monnaie, toutes de même apparence. On admet que dans ce lot
50 pièces sont parfaites, c'est à dire que si on lance une de ces pièces, la probabilité d'obtenir pile est égale à 0,5.
Les 50 autres sont truquées. Pour une pièce truquée, la probabilité d'obtenir pile est égale à 0,75.
Pour une pièce donnée, les lancers sont indépendant les uns des autres.
On désigne par A1 l'événement : "obtenir pile au premier lancer".
On désigne par T l'événement : " la pièce est truquée".
1.Quelle est la
probabilité que la pièce choisie soit truquée ?
P(T )= 0,5.
2. Quelle est la
probabilité d'obtenir pile à ce lancer ?
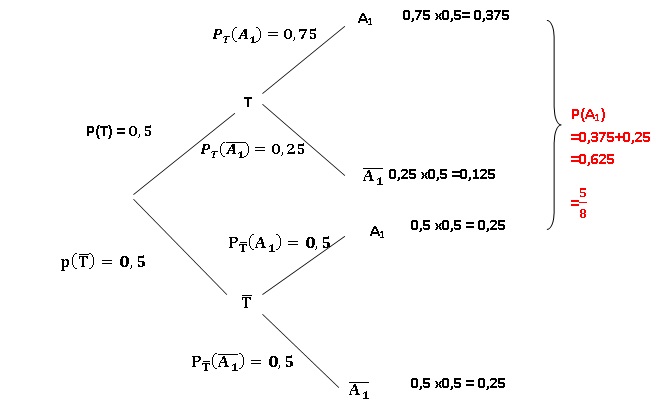
3. Sachant que le résultat du lancer est pile, quelle est la probabilité que la pièce choisie soit truquée ?
0,375 / 0,625 =0,6= 3 / 5.
4. On relance cette même pièce et on obtient de nouveau pile, quelle est la probabilité que la pièce choisie soit truquée ?
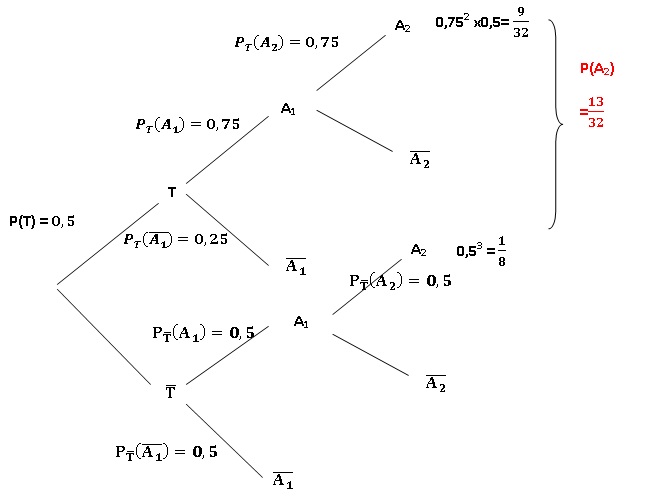
(9 / 32 ) / (13 / 32) = 9 / 13.
|
|
On désire effectuer un tri des pièces
pour éliminer les pièces truquées. Pour cela, on prend les pièces du
lot, une à une, et on lance chaque pièce deux fois. Si on obtient deux
fois pile, on décide d'éliminer la pièce. Dans le cas contraire, on la
conserve.
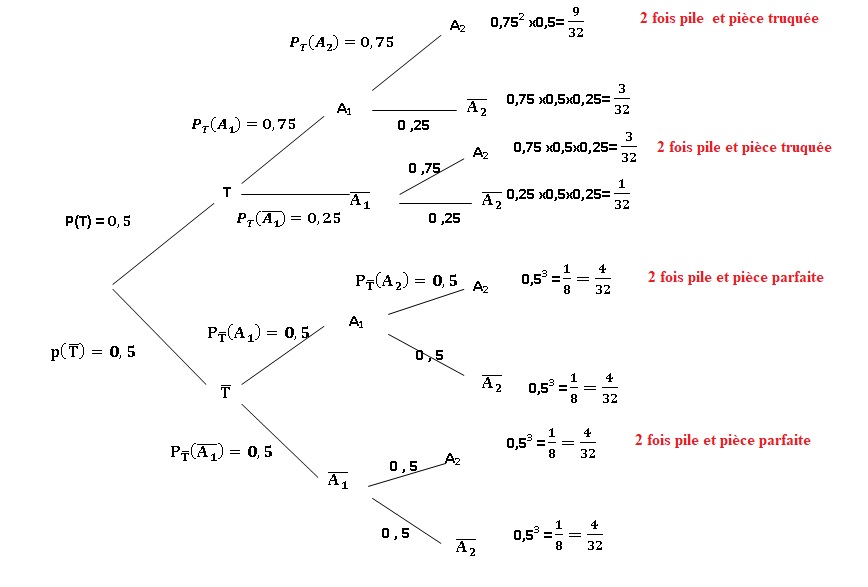
5. Quelle est la probabilité d'éliminer une pièce parfaite ?
Probabilité d'obtenir deux fois pile : (9+3+4+4) / 32 = 20 / 32.
Probabilité d'éliminer une pièce parfaite : 8 / 20 = 2/5 = 0,2.
6. Quelle est la probabilité de conserver une pièce truquée ?
Probabilité de conserver une pièce : (3+1+4+4) / 32 = 12 /32.
Probabilité de conserver une pièce truquée : 4 / 12 = 1,/4.
7. Conclure.
La méthode n'est pas efficace.
|
|