Mathématiques,
physique, concours TSPEI 2014.
Technicien Supérieur Principal de l'Economie et de l'Industrie
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Mathématiques.
Problème 1.
On considère la fonction définie sur
]0 ; +oo[ par f(x) = 0,5 (x + 1 /x).
1. Déterminer les
limites de f(x) si x tend vers l'infini et si x tend vers zéro par
valeur positive. Donner les équations des asymptotes.
Si x tend vers l'infini : 1 /x tend vers zéro et la fonction tend vers
plus l'infini.
La droite d'équation y = 0,5 x est asymptote.
Si x tend vers zéro par valeur positive, 1 / x tend vers plus l'infini
et la fonction tend vers plus l'infini.
La droite d'équation x=0 est asymptote.
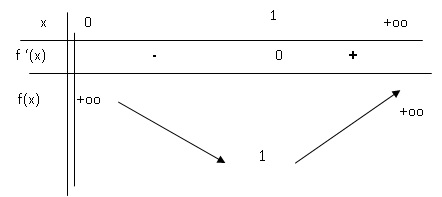
2. Calculer la
dérivée de f et en déduire le tableau de variatios.
f '(x) = 0,5 (1-1 / x2).
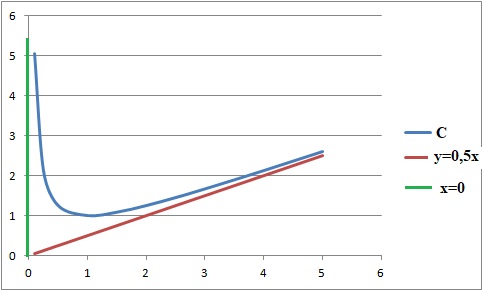
 3. Construire la courbe C et ses asymptotes.
3. Construire la courbe C et ses asymptotes.
5. Montrer que
pour tout x > 1 on
a : 0 < f(x)-1 < 0,5(x-1).
f(x) > 1, donc
f(x)-1 >0.
f(x)-1 -[0,5(x-1)]= 0,5(x+1 / x-2-x+1]= 0,5[1/x-1].
Pour tout x >1,
1/x-1 <0.
Donc f(x)-1< 0,5(x-1).
Soit la suite (un)
définie par u0 = 2 et pour tout entier naturel n, un+1=f(un).
5. Calculer u1
et u2.
u1 = f(u0) = 0,5(2+0,5) = 1,25= 5 / 4.
u2 = f(u1) =
0,5(5/4 +4 /5) = 41 / 40.
6. Montrer que pour
tout entier naturel n, on a :
0 < un-1
< 0,5n.
Initialisation
: 0 < u1-1 < 0,51 ; la
propriété est vraie au rang 1.
Hérédité :
la propriété est supposée vraie au rang p ; 0 < up - 1 < 0,5p.
up+1-1=f(up)-1.
Or
0 < f(x)-1 < 0,5(x-1), donc 0 < up+1-1 <
0,5(up-1).
Or
up - 1 <
0,5p , donc 0,5(up-1)
< 0,5p+1 .
Conclusion
: la propriété étant vraie au rang 1 et héréditaire, elle est vraie
pour tout entier n.
7. Que peut-on en déduire pour la
suite (un) ?
0 < 0,5 <1, donc 0,5n tend vers zéro quand n tend vers
l'infini.
La limite en l'infini de un-1 est égale à zéro.
un tend vers 1 quand n tend vers l'infini.
Problème 2.
Un commerçant reçoit des ampoules livrées par paquets de 6. On admet
que :
le carton d'emballage de 2 % des ampoules est abimé.
60 % des paquets ayant un carton abimé contiennent au moins une ampoule
cassée.
95 % des paquets ayant un carton intact ne contiennent pas d'ampoule
cassée.
On choisit un paquet au hasard parmi la livraison.
On désigne par "D" l'événement " le carton d'embalage est abimé".
On désigne par "C" l'événement " au moins una ampoule est cassée".
1. Calculer la
probabilité des événements suivants :
A1 =" le carton d'emballage est intact".
A2 = " le carton d'emballage est abimé et aucune ampoule
n'est cassée".
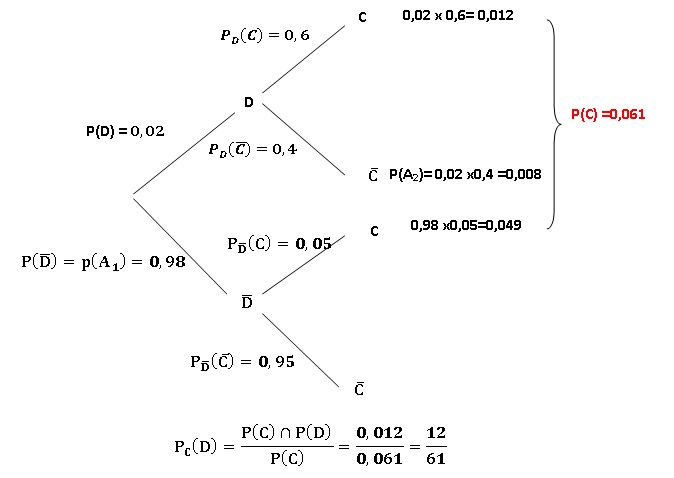
2. Calculer la
probabilité de l'événement C.
3. Sachant qu'un
paquet contient au moins une ampoule abimée, quelle est la probabilité
que le carton d'emballage soit abimé ?
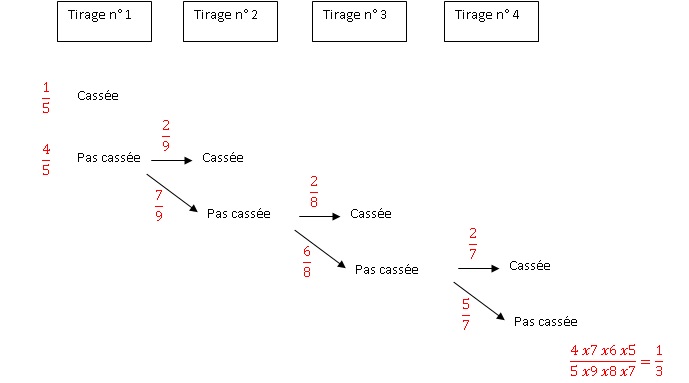
Le
commerçant dispose en stock 10 paquets. Parmi eux, 2 contiennent au
moins une ampoule cassée. Il choisit au hasard 4 paquets parmi ce lot
de 10, ces paquets étant destinés à la vente.
4. Quelle est la
probabilité que ces 4 paquets ne contiennent aucune ampoule cassée ?
.
|
|
|
|
Fission
et fusion nucléaire..
L'uranium enrichi à 3,7 % subit la
réaction de fission :
23592U + 10n
---> 94xSr + 13954Xe +
y 10n.
1.
Déterminer x et y en justifiant.
Conservation du nombre de nucléons : 235+1 = 94 + 139 + y ; y = 3.
Conservation de la charge : 92 = x +54 ; x = 38.
23592U + 10n
---> 9438Sr + 13954Xe
+ 3 10n.
2. Calculer en MeV
l'énergie libérée par la fission d'un noyau d'uranium.
|
noyau
|
23592U
|
9438Sr
|
13954Xe
|
10n
|
21H
|
31H |
42He
|
|
masse (u)
|
235,044
|
93,915
|
138,918
|
1,009
|
2,013
|
3,015
|
4,001
|
1 MeV = 1,6 10-13 J ; c
= 3 108 m/s ; 1 u = 1,67 10-27 kg ; 1 tep
= 42 GJ ; NA = 6,02 1023 mol-1.
Variation de masse Dm =2 m(10n)
+ m(13954Xe) + m( 9438Sr)
- m(23592U)
Dm =
2*1,009 +138,918
+93,915-235,044= -0,193 u
-0,193*1,67 10-27 = -3,22 10-28 kg.
Cette diminution de masse s'acompagne de la libération d'énergie dans
le milieu extérieur ( ce que traduit le signe négatif) :
Dm c2
= -3,22 10-28
*(3 108)2 = -2,90 10-11 J .
-2,90 10-11 / 1,6 10-13
= -1,81 102
MeV.
3. Estimer
l'énergie libérée par la fission d'une masse m = 1,0 kg d'uranium 235.
Nombre de noyaux
d'uranium 235 : 1000 / M(235U) NA
=1000 / 235 x 6,02 1023 ~2,56 1024.
E= 2,90 10-11
x2,56 1024 ~7,4 1013
J.
Fusion de l'hydrogène.
1. L'hydrogène
possède trois isotopes 11H, 21H,
31H.
Ecrire les différentes réactions qui conduisent à la formation d'un
noyau d'hélium accompagné ou non d'une ou plusieurs particules.
11H +31H
---> 42He
21H
+21H ---> 42He.
21H
+31H ---> 42He
+01n.
31H +31H
---> 42He +2 01n.
2. On s'intéresse
à la réaction 21H
+31H ---> 42He
+01n. Déterminer l'énergie E, en joule puis en
MeV, accompagnant la formation d'un noyau d'hélium.
Variation de masse Dm = m(10n)
+ m(42He) - m( 31H)
- m(21H)
Dm = 1,009 +4,001
-3,015-2,013= -0,018 u
-0,018*1,67 10-27 = -3,006 10-29 kg.
Cette diminution de masse s'acompagne de la libération d'énergie dans
le milieu extérieur ( ce que traduit le signe négatif) :
Dm c2 =
-3006 10-29
*(3 108)2 = -2,70 10-12 J .
-2,70 10-12 / 1,6 10-13
= -1,69 101
MeV.
3.
En déduire l'énergie E' libérée par la fusuin d'une masse M = 1,00 kg
de mélange contenant le même nombre d'atomes des deux isotopes. On
négligera la masse des électrons.
Nombre de noyaux de
chaque isotope : 1000 / M(2H +3H)) NA
=1000 / 5 x 6,02 1023 ~1,2 1026.
E= 2,7 10-12
x1,2 1026 ~3,251014
J.
4. Reproduire le tableau ci-dessous
puis cocher les cases correspondantes aux réponses correctes.
|
Fission
|
Fusion
|
Plus
grande abondance des réserves de combustibles
|
|
X
|
Production
moindre de déchets radioactifs
|
|
X
|
Pas
de risque d'emballement des réactions
|
|
X
|
Technologie
utilisée en production industrielle
|
X
|
|
.
|
|
|
|
|
Energie solaire.
Lorsqu'il
est visible, le soleil apporte en moyenne une puissance de 750 W par
mètre carré de surface horizontale. Le rendement des capteurs est de 12
%. On considère que le soleil est visible 30 % du temps.
1. Déterminer
l'énergie récupérable par m2 de surface de capteur pour une
année de 365 jours.
0,3 x365 x24 x3600 =9,46 106 s.
ER =0,12 x750 x 9,46 106 =8,5 108 J m-2.
2. La consommation
moyenne d'un habitant est évaluée à 2 tonnes de pétrole par an et 1 kg
de pétrole fournit en moyenne 4,2 107 J. Calculer
l'énergie E consommée par habitant par an et la surface S de capteurs
nécessaires pour alimenter en énergie une ville d'un million
d'habitants par an.
E = 4,2 107 x2000 =8,4 1010 J par habitant par an
soit 8,4 1016 J pour cette ville.
Surface de capteurs : 8,4 1016 / 8,5 108 ~1 108
m2.
3. En fait,
l'ensemble des capteurs utilisés permet de recueillir par an, sous
forme électrique, une énergie de 1,2 1017
J. Cette énergie est transportée vers la ville par une ligne électrique
sous une tension efficace de 200 kV. Le facteur de puissance est 0,95.
Calculer la puissance électrique et l'intensité efficace du courant
électrique circulant en moyenne dans cette ligne.
Puissance(W) = énergie(J) / durée (s) =1,2 1017 /(365
x 24 x 3600) =3,8 109 W.
I = P /(0,95 U) = 3,8 109 /(0,95 x200 000)=2,0 104
A.
4. La ligne a une
longueur de 40 km. On ne veut pas perdre plus de 10 % de l'énergie
transportée par effet Joule. Calculer la résistance maximale de 1 km de
ligne.
Pjoule =r I2 = 3,8 108 W.
r =3,8 108 / (4 108)=0,95 ohm soit 0,95 / 40
~0,024 ohm par km.
Dispositif de chauffage.
Captée à la
température q1
= 15°C, l'eau doit chauffer à la température finale q2 = 85 °C. Le
dispositif est prévu pour préchauffer M = 1000 kg d'eau par heure. Ceau
= 4190 J kg-1 K-1. La chaudière produit une masse
m de vapeur d'eau par heure. Cette vapeur pénètre dans l'eau à
préchauffer dans un échangeur parfaitement calorifugé. La vapeur
condensée sort à 85°C.
1. Calculer la quantité de chaleur Qeau
absorbée par 1000 kg d'eau dont la température passe de 15 à 85 °C. En
déduire la puissance calorifique reçue par l'eau à réchauffer.
Qeau = 4190 x 1000 (85-15)=2,93 108 J h-1.
( 2,93 105 kJ h-1).
Peau = 2,93 108 / 3600 = 8,15 104 W.
2. Donner
l'expression de la quantité de chaleur Q1 échangée par une
masse m de vapeur d'eau qui passe de l'état gazeux à l'état liquide à
100°C. La chaleur latente de liquéfaction de l'eau est L = 2257,2 kJ kg-1.
Q1 = m L = 2257,2 m (kJ).
3. Donner
l'expression de la quantité de chaleur Q2 échangée par la masse d'eau m
provenant de la liquéfaction de la vapeur en passant de 100°C à 85°C.
Q2 = 4,19 m(100-85) =62,85 m ( kJ).
4. On considère le
système formé par la masse M d'eau et la masse m de vapeur. On
considère que ce système est adiabatique. Ecrire l'a relation liant Qeau,
Q1 et Q2. En déduire m.
Qeau= Q1 + Q2.
2,93 105 = (2257,2 +62,85)m ; m = 126,3 kg.
5. La chaleur est fournie par la combustion du fuel. Chaque kilogramme
de fuel libère 4,2 104 kJ. Le rendement de la chaudière est
de 80 %. Calculer la consommation horaire de fuel.
4,2 104 x0,8 = 3,36 104 kJ.
2,93 105 / (3,36 104) =8,72 kg h-1.
|
|
|



