Mathématiques,
physique,
concours TSPEI 2013.
Technicien Supérieur Principal de l'Economie et de l'Industrie
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Probabilités.
Une
usine fabrique des produits chimiques. Elle comprend 2 parties :
l'unité A et l'unité B. Les produits sont fabriqués dans l'unité A et
stockés dans l'unité B. L'unité A ouvre sur l'unité B et celle-ci
ouvre sur l'extérieur.
La droite d'équation y =
0,5 x est asymptote.
Un nuage de polluants N est émis au sein de l'unité A à l'instant t=0. Soit n un entier naturel.
On admet que, à tout instant t = n, le nuage N ne peut occuper que l'une des trois positions suivantes :
au sein de l'unité A ; au sein de l'unité B ; à l'extérieur de l'usine.
La position du nuage obéit aux règles suivantes :
Lorsque le nuage est dans l'unité A à l'instant t = n alors, à
l'instant t=n+1, soit il reste dans l'unité A avec une probabilité de 1
/ 3, soit il est dans l'unité B avec une probabilité 2 / 3.
Lorsque le
nuage est dans l'unité B à l'instant t = n alors, à l'instant t=n+1,
soit il reste dans l'unité B avec une probabilité de 1 / 2, soit il est
dans l'unité A avec une probabilité 1 / 4, soit il est à l'extérieur de l'usine avec une probabilité x..
Lorsque le nuage est à l'extérieur de l'usine à l'instant t = n, alors à l'instant t > n, il reste à l'extérieur.
Pour tout n on note :
An, l'événement "le nuage est dans l'unité A à l'instant t =n".
Bn, l'événement "le nuage est dans l'unité B à l'instant t =n".
Cn, l'événement "le nuage est à l'extérieur à l'instant t =n".
1. Déterminer le réel x..
P(An+1) + P(Bn+1) + P(Cn+1) = 1 ; x = 1 / 4.
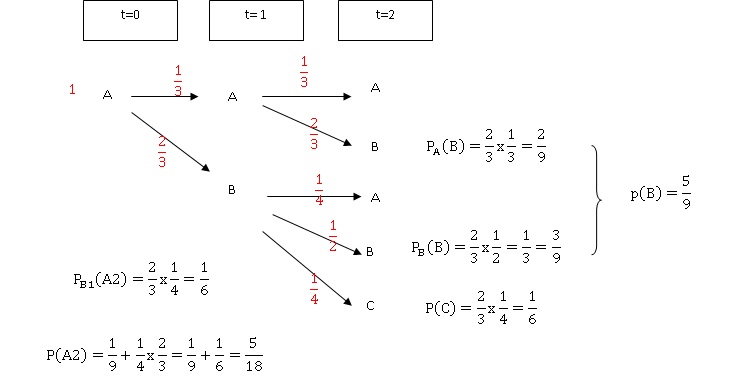
2. Quelle est la probabilité , qu'à l'instant t = 1, le nuage soit dans l'unité A ?
A l'instant t=0, le nuage est dans l'unité A. P(A1 ) = 1 / 3.
3.a.
Déterminer la probabilité, qu'à l'instant t=2, le nuage soit dans
l'unité B sachant qu'il était dans l'unité A à l'instant t =1.
3.b. Calculer la probabilité que le nuage soit dans l'unité B à l'instant t = 2.
4. calculer la probabilité que le nuage soit à l'extérieur à l'instant t = 2.
5. Sachant qu'à l'instant t=2, le nuage est dans l'unité A, qu'elle est la probabilité qu'il fût dans l'unité B à l'instant t=1 ?
Fonction.
On considère la fonction définie sur R par : f(x) = (3ex-1) / (ex+1).
1. Calculer f(0) et f(1).
f(0) = (3-1) / (1+1) = 1 ; f(1) = (3e-1) / (e+1).
2. Déterminer la limite de f en plus l'infini et en moins l'infini.
f(x) = (3-1/ex) / (1+1 / ex).
Quand x tend vers plus l'infini : 1 / ex tend vers zéro et donc f(x) tend vers 3.
Quand x tend vers moins l'infini : ex tend vers zéro et donc f(x) tend vers -1.
3. Calculer la dérivée de f(x) et en déduire le tableau de variations de f(x).
On pose u = 3ex-1 et v = ex+1 ; u' = 3ex ; v' = ex ;
f '(x) = (u'v-v'u) / v2 =[ 3ex(ex+1) -ex(3ex-1)] / (ex+1)2=4ex./ (ex+1)2.
f '(x) étant positive, f(x) est strictement croissante
4. Monrer que la courbe représentant f(x) coupe l'axe des abscisses en un point unique dont on donnera les coordonnées.
f(x) = 0 soit 3ex-1 = 0 ; ex = 1 /3 ; x = ln(1/3) = -ln(3).
L'équation f(x) = 0 admet une seule solution.
Coordonnées du point d'intersection de la courbe avec l'axe des abscisses ( -ln(3) ; 0 ).
4. Déterminer une équation de la tangente à la courbe au point d'abscisse zéro.
Coefficient directeur de la droite : f ' (0) =4e0./ (e0+1)2 = 1.
La tangente pase par le point de coordonnées ( 0 ; f(0) = 1 )
Equation de la tangente y = x+1.
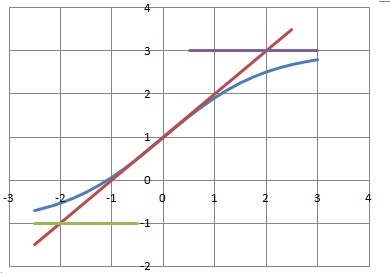
5. Tracer la courbe, la tangente au point d'abscisse zéro et la asymptotes.
|
|
|
|
Physique..
Une
raffinerie doit transporter des produits bitumineux à forte viscosité
qui sont liquides à 180°C. La solution retenue est la canalisation dite
tube à passage de courant ou TPC.
Longueur de la ligne 405 m ; diamètre 154,1 mm ; tube acier ; calorifuge : laine de roche.
Bitume : température initiale 0°C ; température de fonctionnement 180°C ; masse volumique r = 1050 kg m-3 ; capacité thermique massique c = 2930 J kg-1 °C-1 ; temps de préchauffage : 5 jours.
Alimentation électrique TBTS ( 50 V).
Pour la phase de préchauffage:
1. Calculer le volume V puis la masse m de bitume contenue dans une ligne.
V = longueur fois section = 405 x3,14 x0,15412 / 4 = 7,55 m3 ;
m = rV = 1050 x7,55 ~7,93 103 kg.
2. Calculer l'énergie thermique Q nécessaire pour amener le bitume de 0 à 180°C.
Q = mc Dq = 7,93 103 x 2930 x180 =4,18 109 J.
3. Le rendement énergétique étant de 90 %, calculer l'énergie électrique We consommée pour chauffer le bitume.
We = Q / 0,9 = 4,18 109 / 0,9 =4,65 109 J.
4. En déduire la puissance électrique Pe.
Pe = We / durée (s) = 4,65 109 /(5 x24 x3600)=1,08 104 W.
5. Calculer l'intensité du courant qui circule dans le tube.
I = Pe / U = 1,08104 / 50 = 215 A.
Exercice 2.
Un ressort de raideur k = 4,0 103 N m-1,
à spires non jointives, est relié à une masse m=100 kg. Le solide esr
relié à une extrémité du ressort et guidé par une tige horizontale. Les
frottements sont négligés. On écarte le solide de sa position
d'équilibre et on le lâche sans vitesse à la date t=0. Son abscisse est
alors x0 = 5,0 10-2 m.
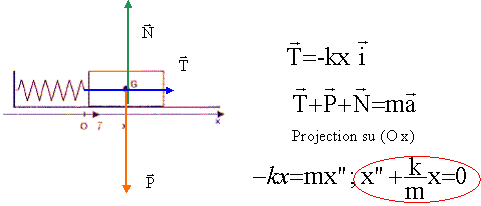
1. Faire le bilan des forces s'exerçant sur le solide et les représenter sur un schéma.
2. Etablir l'équation différentielle du mouvement.
Le solide est soumis à son poids, à l'action de la tige et à l'action de rappel du ressort.
3. Calculer la période propre T0 des oscillations.
w0 = (k / m)½ ; T0 = 2p /w0 = 2p(m / k)½ = 6,28(100 / 4000)½ =0,993 ~0,99 s.
4. Etablir l'équation horaire du mouvement.
x(t) = x0 cos (w0t).
x(t=0) = x0 ; x'(t) = -x0 w0 sin (w0t) ; x'(t=0) = -x0 w0 sin 0 = 0.
5. Donner
l'expression de l'énergie cinétique, de l'énergie potentielle élastique
du système. Retrouver l'équation différentielle à partir de la
conservation de l'énergie.
Ec = ½m x'2 = ½m (x0 w0)2 sin2 (w0t)
Ep = ½kx2 = ½k (x0 )2 cos2 (w0t).
En absence de frottement l'énergie mécanique du système se conserve. Ec + Ep = constante.
½m x'2 +½kx2 =Cste.
Dériver par rapport au temps : m x' x" + k x' x = 0.
Soit m x" +kx = 0.
|
|
|
|
|
Exercice 3.
De
l'eau sous pression circule dans le circuit primaire fermé d'une
centrale nucléaire. Elle se réchauffe lors de son passage dans le coeur
du réacteur grâce à l'énergie produite par les éléments combustibles.
Cette énergie calorifique, transportée par l'eau sous pression, est
utilisée via l'échangeur, par le circuit secondaire pour produire de
l'énergie électrique. On considère que tous les points du corcuit
primaire sont à la même altitude.
Débit de l'eau Qm =13,2 103 kg s-1 ;
diamètre de la conduite D = 600 mm ; longueur de la conduite L=9 m ;
les deux coudes sont équivalents pour les pertes de charge à une
longueur de 2 m ; viscosité cinématique de l'eau n = 5,0 10-7 m2 s-1.
1. L'une des réaction possible est :
23592U +10n ---> 139ZI +9439Y +x10n.
Cette réaction est-elle une réaction de fission, de fusion ou de désintégration spontanée ? Justifier.
En bombardant l'uranium 235 par des neutrons, le noyau 23592U se brise en deux nouyaux fils et en neutrons. C'est une réaction de fission.
2. Déterminer Z et x en rappelalnt les lois utilisées.
Conservation de la charge : 92 = Z +39 soit Z = 53.
Conservation du nombre de nucléons : 235+1=139+94+x soit x = 3.
3. Calculer le débit volumique de l'eau dans le circuit primaire.
Qv = Qm / reau = 13,2 103 / 1000 = 13,2 m3 s-1.
4. Montrer que la vitesse de l'eau dans la conduite est v = 46,7 m s-1.
Section S = pD2 / 4 = 3,14 x0,62 / 4 =0,2827 m2 ; v = Qv / S = 13,2 / 0,2827 = 46,7 m s-1.
5. Calculer le nombre de Reynolds dans cette conduite et en déduire le type d'écoulement.
Re = v D / n = 46,7 x0,6 / (5,0 10-7) = 5,6 107.
Ce nombre étant supérieur à 105, l'écoulement est turbulent rugueux.
6. Que vaut le coefficient de pertes de charge linéaire l dans la conduite ?
l = 3,5 10-2, indépendant de Re.
7. Calculer les pertes de charge linéaire ( en m) dans la conduite. En déduire la variation de pression correspondante.
J = lv2L / (2Dg) =3,5 10-2 x46,72 x11/(1,2 x9,8)=71,4 m.
DP = peau g J = 1000 x9,8 x71,4 ~7 105 Pa.
|
|
|


