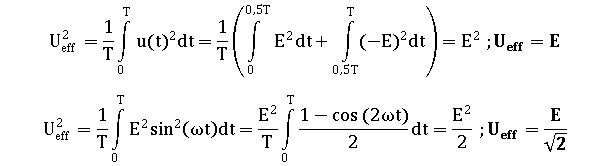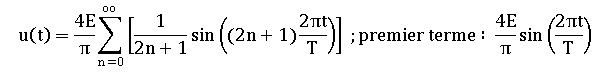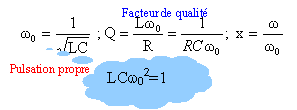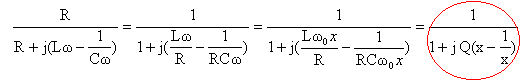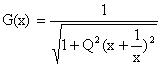L'effet
photovoltaïque, onduleur.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Découvert
en 1839 par A. Becquerel, l'effet photovoltaïque permet la
transformation de l'énergie lumineuse en énergie électrique. Lorsqu'un
photon suffisamment énergétique frappe la jonction PN au niveau de la
bande de déplétion, il fait passer un électron de la bande de valence à
la bande de conduction, et crée ainsi une paire électron libre - trou
libre. Sous l'action du champ électrique dans la zone de déplétion,
l'électron et le trou vont se déplacer dans le semi-conducteur. Les
cellules photovoltaïques fonctionnent sur ce principe.
25.
Exprimer l'énergie d'un photon en précisant le nom et l'unité de chaque
terme. Après avoir rappelé l'intervalle des longueurs d'onde dans le
vide correspondant à la lumière visible, exprimer les énergies minimale
et maximale des photons pour la lumière visible.
E = h v = h c / l.
h : cponstante de Planck ; v
: fréquence en Hz ; l
: longueur d'onde ( m) ; c : célérité de
la lumière dans le vide ( m / s).
Les longueurs d'onde du visible sont comprises entre 400 ( bleu) et 800
nm ( rouge ).
Emini = 6,62 10-34 x 3 108 /(800 10-9)
=2,48 10-19 J ou 1,55 eV.
.Emaxi
= 6,62 10-34 x 3 108 /(400 10-9) =4,96
10-19 J ou 3,10 eV.
26.
Comparer l'énergie de gap du silicium ( 1,11 eV ) aux valeurs des
énergies des photons de la lumière visible. Quelle en est la
conséquence lorsqu'une jonction est éclairée par de la lumière visible ?
Les énergies des photons de la lumière visible sotn supérieures au gap
du silicium. Ils sont donc tous absorbés.
27.
Représenter le champ électrique en différents points de la zone de
déplétion, ainsi que les forces électriques subies par un électron ou
un trou qui serait situé dans cette zone.
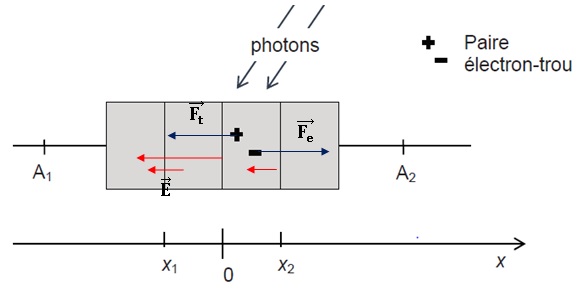
28
Lorsqu'on place une résistance aux bornes de la jonction PN, on
constate que celle-ci est traversée par un courant électrique.
Expliquer l'origine de ce courant. Indiquer son sens.
Des
paires d'électrons trous sont créées au niveau de la jonction lors de
l'absorption des photons. Sous l'action du champ électrique, les trous
se déplacent vers la gauche et les électrons vers la droite. D'où
l'existence d'un courant électrique i.
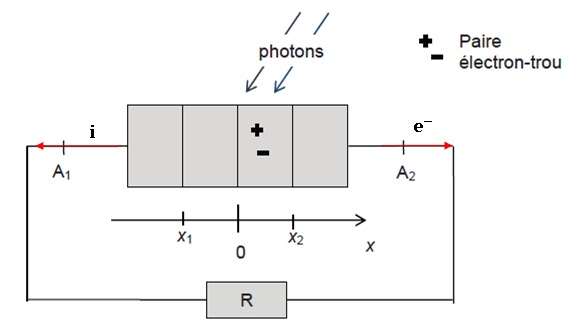
La cellule photovoltaïque.
Les caractéristiques tension-intensité d'une cellule photovoltaïque
obtenues pour différentes valeurs de la puissance surfacique lumineuse
reçue sont données. La température de la cellule est maintenue à 25 °C.
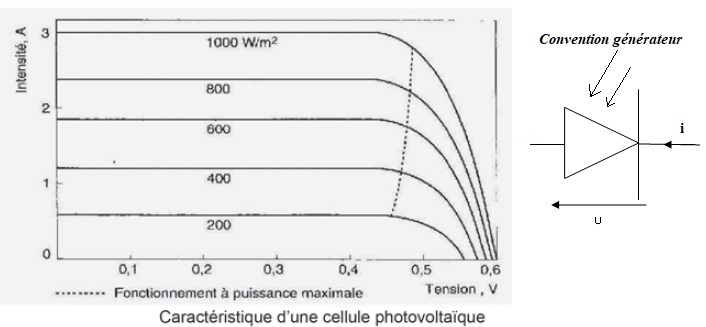
29. Préciser sur le
symbole normalisé de la cellule ( diode de jonction ), les conventions
d'orientation de l'intensité et de la tension.
|
...
|
|
30.
Pour une puissance surfacique de 1000 W m-2,
déterminer à partir de la figure :
- la tension à vide U0 aux bornes de la cellule en circuit
ouvert.
- l'intensité Icc du courant électrique qui traverse la
cellule lorsqu'elle est en court-circuit.
U0 = U ( I = 0) = 0,6 V ; Icc= I( U = 0) = 3 A.
31. Recevant une
puissance surfacique de 1000 W m-2,
la cellule alimente une résistance de valeur R. Déterminer R pour
que la puissance fournie à la résistance soit maximale.
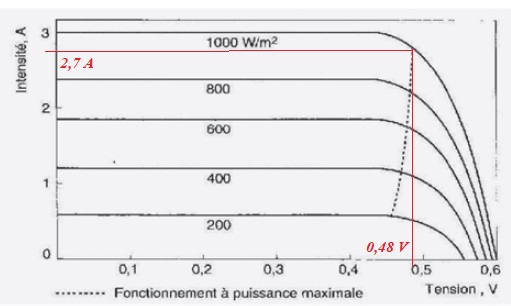
R = 0,48 / 2,7 ~0,18 ohm.
Les cellules sont assemblées pour donner des panneaux photovoltaïques.
On donne les caractéristiques du panneau pour plusieurs valeurs de la
puissance surfacique d'ensoleillement.
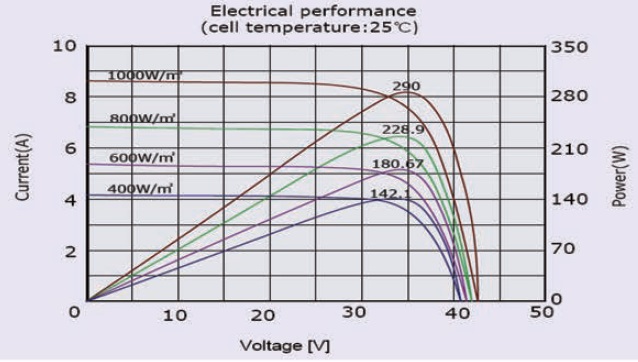
32. Indiquer en
justifiant comment sont associées les cellules photovoltaïques pour
obtenir un panneau photovoltaïque. Faire un schéma de cette association.
Icc total = 9 A = 3 Icc ; U0 total
~42 V = 70 U0.
On associe 70 cellules en série. On monte en parallèle 3 fois 70
cellules en série.
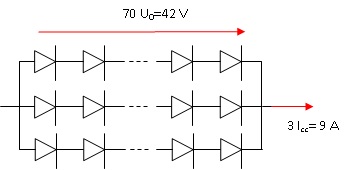
33. Proposer une
activité expérimentale réalisanle en classe de Sti2d,en lien avec les
trois questions précédentes.
But :
déterminer le rendement nominal d'un panneau solaire ?
Matériel :
un panneau solaire, un projecteur, une résistance variable de 1 à 100
ohms , un luxmètre, un voltmètre, un ampèremètre, des fils, un
ordinateur équioé d'un tableur grapheur comme régressi.
Résultats :
tracer la caractéristique I = f(U) ou P = f(U) ; en déduire la
puissance nominale.
Le luxmètre donne la puissance surfacique reçue par le panneau.
Mesure les dimensions du panneau pour déterminer sa surface.
Calculer le rendement et conclure.
|
....
|
Des panneaux photovoltaïques au réseau
électrique.
Un
onduleur permet de transférer l'énergie électrique des panneaux
photovoltaïques, source d'énergie électrique continue, à une charge
fonctionnant en alternatif. L'énergie électrique ainsi produite est
directement consommée par le propriètaire de l'installation ou délivrée
à un réseau de distribution. Cette partie étudie le principe de
fonctionnement d'un onduleur.
34.
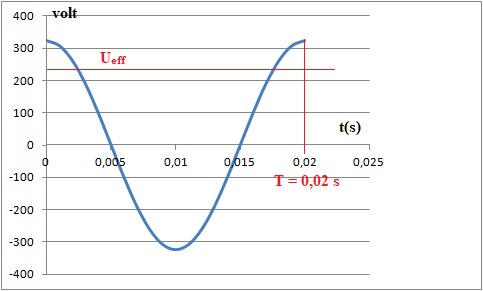
Donner les caractéristiques électriques de la tension v délivrée par
EDF : fréquence, valeur efficace, amplitude. Tracer son chronogramme
v(t).
Valeur efficace : 230 V ; fréquence : 50 Hz ; période 0,02 s ;
amplitude 230 x2½~325 V.
Le schéma du circuit électrique modèlisant l'onduleur est ke suivant :
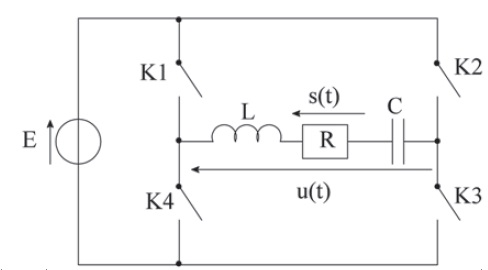
E est la force électromotrice constante et positive d'une source de
tension idéale.
La commande des interrupteurs que l'on suppose parfaits est la suivante
:
pour 0 < t < 0,5 T, K1 et K3 sont fermés et
K2 et K4 sont ouverts.
pour 0,5T < t < T, K1
et K3 sont ouverts et K2 et K4 sont
fermés.
35.
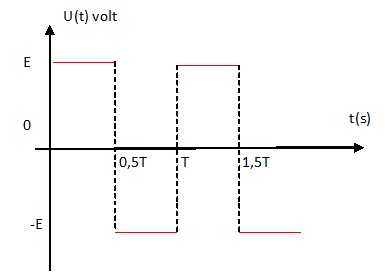
Tracer le chronogramme de la tension u(t).
Pour 0 < t < 0,5 T, u(t) = E.
Pout 0,5 T < t < T, u(t) = -E.
36.
Définir la valeur efficace d'un signal périodique quelconque puis
établir la valeur efficace de la tension u(t) en fonction de E.
Comparer à la valeur efficace d'un signal sinusoïdal d'amplitude E.
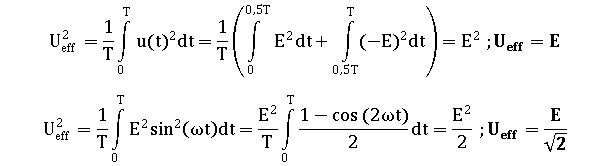
37.
La décomposition en série de Fourier de u(t) s'écrit :
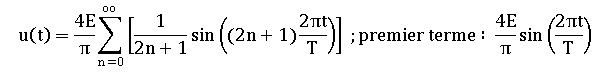
Comment appelle-t-on le premier terme et les termes suivants ?
Justifier que cette décomposition ne fait apparaître que des fonctions
sinus.
Le premier terme est le fondamental et les termes suivants sont les
harmoniques.
u(t) est une fonction impaire : sa décomposition en série de Fourier ne
comporte que des fonctions imapires, donc des fonctions sinus.
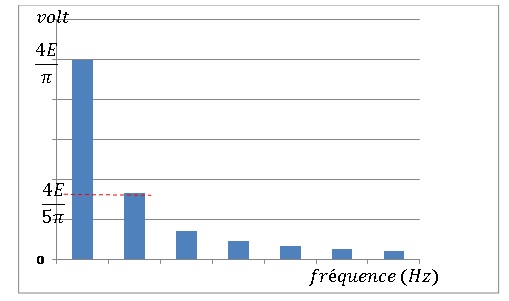
38. Représenter le
spectre en amplitude de la fonction u(t).
Justifier que l'association RLC est un filtre qui permet d'obtenir en
sortie une tension u(t) sinusoïdale similaire à celle du réseau EDF
avec en entrée la tension u(t). Nommer le filtre et représenter
l'allure de son diagramme de Bode.
Fréquence du fondamental f1 ; fréquence des harmoniques : fn
= (2n+1) f1.
Amplitude des harmoniques : 4E / (p (2n+1)).
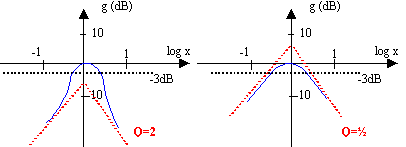
Le circuit RLC est un filtre passe bande ; s(t) = uR(t) et
e(t) = uR(t) + uL(t) +uc(t).
Fonction de transfert complexe : H(jw) = R / (R + j(Lw-1/(Cw)).
On pose : 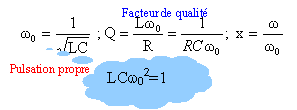
H(jw) = s / e
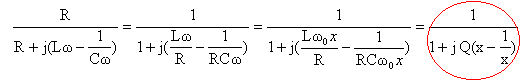
expression du gain G(w): norme de la fonction de transfert
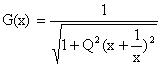
g = 20 log G(x) = -10 log [ 1+Q²(x-1/x)²], g exprimé en
décibel (dB)
recherche des asymptotes :
lorsque x tend vers 0+, g tend vers moins
l'infini
1 est négligeable devant Q²/ x²
g équivalent à : -20 logQ + 20
log x équation de l'asymptote.(pente 20 dB
par décade)
lorsque x tend vers l'infini, g tend vers moins l'infini
:
1 est négligeable devant Q²x²
g équivalent à : -20 logQ - 20
log x équation de l'asymptote.(pente -20
dB par décade)
|
39. Sur
un toit orienté au sud-est et incliné de 30° par rapport à
l'horizontale ( facteur de correction 0,96 ), un particulier a installé
10 panneaux photovoltaïques dont les caractéristiques sont données
ci-dessus.
A
partir des données ci-dessous, estimer l'énergie maximale que pourra
produire ce particulier au cours d'une journée en considérant qu'un
système de régulation permet au panneau de délivrer une puissance
maximale. Détailler les calculs.
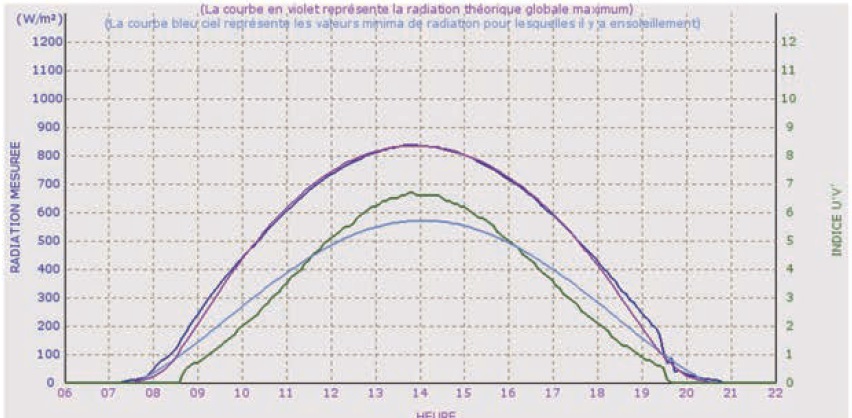
Entre 8 h et 14 heures la puissance surfacique croît de manière à peu
près linéaire ; elle décroît de 14 h à 20h de manière à peu près
linéaire.
Puissance moyenne reçue par les panneaux solaires : Pmoy =
1/(20-8) ( 800 (14-8) / 2 +800 (20-14) / 2)= 400 W m-2.
Puissance crète correspondante : 142,1 W.
Tenir compte du facteur de correction : 0,96 x142,1 ~136 W.
Energie totale : 136 x10 x24 ~3,3 104 Wh = 33 kWh par jour.
|
|
|