La
jonction P-N.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Diffusion d'impuretés.
Pour
augmenter le nombre de porteurs mobiles dans le silicium et modifier
ses propriétés électriques, on introduit dans le cristal, de façon très
précise, des atomes différents du silicium, qu'on qualifie d'impuretés.
On dit alors que l'on effectue un dopage et que le semi-conducteur est
dopé. Le dopage s'effectue par un phénomène de diffusion qui a lieu à
température élevée. Lorsque le système est ramené à température
ambiante, les impuretés sont alors figées.
On note c(M,t) la concentration en impuretés en un point M à un instant
t.
L'inhomogénéité en concentration entraîne un mouvement des impuretés
caractérisé par un vecteur densité de courant de particules 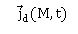
10.
En 1885, A. Fick a proposé une loi de diffusion ; elle fait apparaître
un coefficient de diffusion D de l'impureté dans le semi-conducteur.
Son expression mathématique est :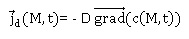
Interpréter cette loi en précisant les unités de chaque grandeur.
Les impuretés se déplacent des zones les plus concentrées vers celles
qui le sont le moins. Il en résulte un courant d'impuretés de sens
contraire au gradient de concentration.
D : diffusivité e m2 s-1; jd : m-2
s-1; c en m-3.
Le semi-conducteur est assimilé à un milieu homogène et on suppose la
diffusion unidirectionnelle.

On note c(x,t) la concentration en impuretés.
11.
Dans un volume élémentaire de section S et d'épaisseur dx, situé entre
les abscisses x et x +dx, effectuer le bilan de matière portant sur les
impuretés afin d'établir une relation entre 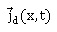 et c(x,t). Ce bilan traduit la conservation du nombre
d'impuretés. et c(x,t). Ce bilan traduit la conservation du nombre
d'impuretés.
Pendant la durée dt :
impuretés entrant dans ce volume : jd (x,t) Sdt
impuretés sortant du volume : - jd
(x+dx,t) Sdt.
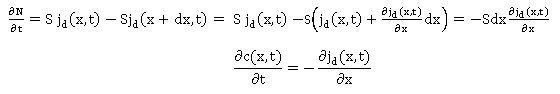
12. En déduire l'équation de
diffusion.
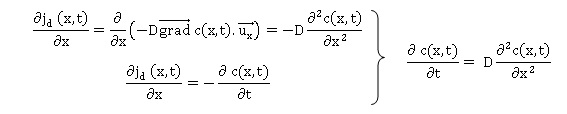
A l'instant t = 0, la concentration en impuretés est nulle en tout
point du semi-conducteur. On note N0
le nombre d'impuretés par unité de surface introduites à partir de
l'instant initial en x=0 à la surface du semi-conducteur considéré
comme semi-infini de x=0 à x = +oo.
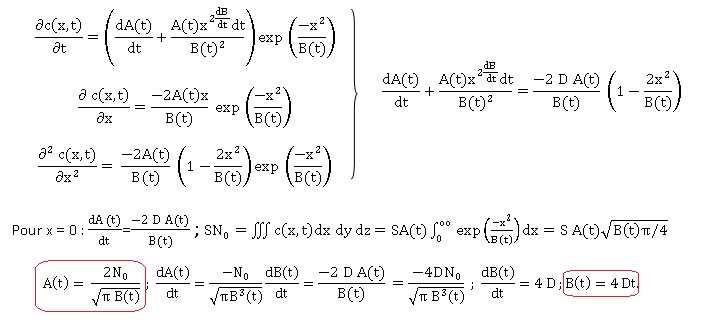
13. On cherche pour
t >0, une solution de l'équation de diffusion sous la forme :
c(x,t) = A(t) exp(-x2 / B(t)).
Déterminer les expressions de A(t) et de B(t) en détaillant les calculs.
 On admettra par la
suite : c(x,t) = N0 (pDt)-½ exp(-x2
/ (4Dt)).
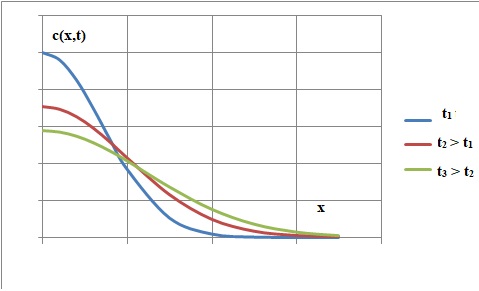
14.
Tracer l'allure de la concentration c en fonction de x à deux instants t1
et t2 > t1.
On admettra par la
suite : c(x,t) = N0 (pDt)-½ exp(-x2
/ (4Dt)).
14.
Tracer l'allure de la concentration c en fonction de x à deux instants t1
et t2 > t1.
15. A une date t0
fixée, à quelle profondeur d
la concentration est-elle moitié de celle en x=0 ? Exprimer d en fonction de D et t0.
Le coefficient de diffusion du phosphore dans le silicium à 1000 °C est
D = 3 10-14 cm2 s-1. Calculer d au bout d'une heure.
c(0, t0) = N0 (pDt0)-½
c(d,t0) = N0
(pDt0)-½
exp(-d2
/ (4Dt0))= 0,5 N0
(pDt0)-½.
ln(2)=d2 / (4Dt0)
; d = 2(Dt0
ln(2))½.
d = 2 (3 10-14
x3600 x ln(2))½ =1,73 10-5 cm =173 nm.
|
...
|
|
Dopage N et P du silicium.
Si les impuretés augmentent la concentration en électrons libres dans
le semi-conducteur, on dit que les impuretés sont de type N et que le
semi-conducteur est de type N. l'atome d'impureté se substitue alors à
un atome de silicium dans le réseau cristallin en apportant un électron
de plus à l'atome qu'il remplace. On note c- la nouvelle
concentration en électrons libres et on néglige la concentration en
trous.
Si les impuretés augmentent la concentration en trous dans le
semi-conducteur, on dit que les impuretés sont de type P et que le
semi-conducteur est de type P. L'atome d'impureté apporte un électron
en moins que l'atome qu'il remplace dans le réseau cristallin. On note c+
la nouvelle concentration en trous et on néglige la concentration en
électrons libres.
16. Déterminer la
nature des impuretés utilisées pour réaliser un dopage de type N et un
dopage de type P. Donner un exemple pour chaque type de dopage.
Dopage de type N : les impuretés doivent possèder un électron de plus
sur leur couche externe. ( phosphore ou arsenic).
Dopage de type P : les impuretés doivent posséder un électron de moins
sur leur couche externe ( bore ou aluminium).
17. Exprimer les
conductivités électriques s'
( respectivement s")
du semi-conducteur dopé N ( respectivement P) en fonction de c- (
respectivement c+), e et µn ( respectivement µp).
Calculer les valeurs numériques pour c- = c+ = 5 1014
cm-3. ( 5 1020 m-3 ) Commenter.
s' = -µn
e c- =1500 10-4 x1,6 10-19 x5 1020 =12
V A-1 m-1.
s'' = µp e c+
=475 10-4 x1,6 10-19 x5 1020 =3,8 V A-1
m-1.
Ces valeurs sont bien supérieures à la conductivité du silicium pur.
|
....
|
La jonction PN à l'équilibre.
On crée une jonction PN en dopant différemment deux parties d'un
matériau semi-conducteur, un dopage de type P pour une partie, un
dopage de type N pour l'autre.
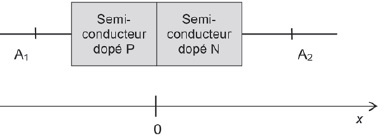
Les électrons de la partie du semi-conducteur dopée N diffusent dans la
partie du semi-conducteur dopée P où la concentration en électrons
libres est plus faible. De même les trous de la partie du
semi-conducteur dopée P diffusent dans la partie du semi-conducteur
dopée N car la concentration en trous y est plus faible. Lorsque la
jonction n'est plus traversée par aucun courant, il s'établit alors un
état d'équilibre.
18. Une fois
l'équilibre atteint :
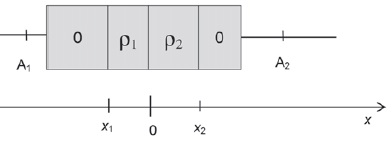
- la région [x1 ; 0] avec x1 < 0 est chargée
avec une densité volumique algébrique de charge uniforme r1 ;
- la région [0 ; x2 ] avec x2
> 0 est chargée avec une densité volumique algébrique de charge
uniforme r2
;
- en dehors de la zone [x1 ; x2 ], appelée zone
de déplétion, la densité de charge volumique est nulle.
Justifier que dans la zone de déflétion, à l'équilibre, les signes des
densités volumiques de charges sont respectivement r1 < 0 et r2 >0. Les
charges qui la constituent sont-elles fixes ou mobiles ?
Les électrons du semi-conducteur dopé N diffusent vers la gauche
et se combinent aux trous du semi-conducteur dopé P. Il en résulte des
cations de charge +e dans la zone dopée N et des anions de charge -e
dans la zone dopée P. Dans la zone de déplétion, les charges portées
par les ions sont fixes ; il n'y a pas de charges libres.
r1
< 0 ; r2
>0.
19. Etablir, en
exprimant la neutralité de la zone de déplétion, une relation entre r1, r2, x1
et x2.
r1
x1 = r2
x2.
20.
La présence d'une distribution volumique de charges dans la zone de
déplétion se traduit par l'existence d'un champ électrique. Dans le
silicium, les lois de l'électrostatiques s'appliquent en remplaçant e0 par e0 er où er
est la permitivité relative du silicium. De plus la largeur de la zone
de déplétion est très faible devant les dimensions du semi-conducteur.
On négligera donc les effets de bords dans les directions orthogonales
à l'axe Ox. Justifier que le champe électrique puisse s'écrire 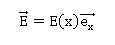 dans la jonction. dans la jonction.
La distribution de charges reste invariante par une tranlation suivant
Oy et Oz. le champ est indépendant de y et z.
La distribution de charges est symétrique par rapport aux plans xOy et
xOz ; le champ est donc contenu dans ces plans.
On admet que le champ électrique est nul dans la zone x < x1.
21.
Exprimer le champ électrique en tout point puis tracer l'allure E(x) en
fonction de x. Justifier alors l'existence d'un équilibre à la jonction.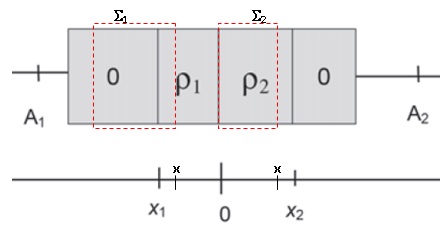
Appliquer le théorème de Gauss sur les surface S1 et S2 :
S E1(x) = S r1
(x-x1) / (e0 er
) ; E1(x) = r1 (x-x1)
/ (e0
er
)
S (E2(x) -E2(0))= S r2 x /
(e0
er
) ; E2(x) = (r2 x-r1x1)
/ (e0
er
)= (r2
x-r2x2)
/ (e0
er
).
Dans la zone de déplétion, le champ électrique est dirigé vers la
gauche. Ce champ croît au fur et à mesure de la migration des
électrons. Ces derniers sont soumis à une force dirigée vers la droite.
C'est l'inverse pour les trous. On aboutit à un équilibre.
|
22. Rappeler
la relation entre le potentiel V et le champ électrique en régime
stationnaire. Exprimer le potentiel électrique puis tracer son allure
en fonction de x On choisit V(x=0) = 0.
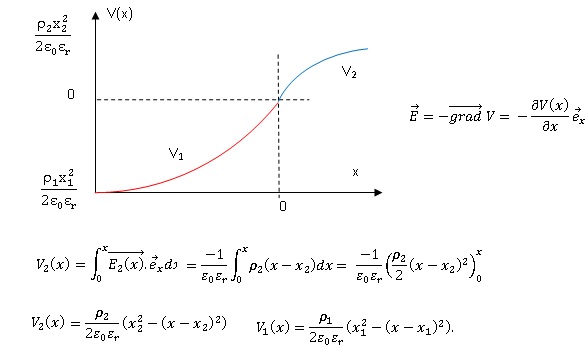
23. Exprimer la
différence de potentiel Ud = VA2-VA1
entre les bornes A1 et A2 puis la calculer pour r1 = -1,0 102
C m-3, r2
= 3,0 104 C m-3 et x1 = - 1,1 µm.
er = 11,7 SI.
Le champ électrique étant nul en dehors de
la jonction, le potentiel y est constant.
Ud = V(x2)-V(x1) = (r2 x22
-r1 x12)
/ (2e0er).
x2 =r1
x1 / r2
=1,1 / (3 102)=0,0037 µm.
Ud = (3,0 104 x(3,7 10-9)2+1,0
102 x(-1,1 10-6)2) x 36 p 109 / (2 x11,7)
~0,6 V.
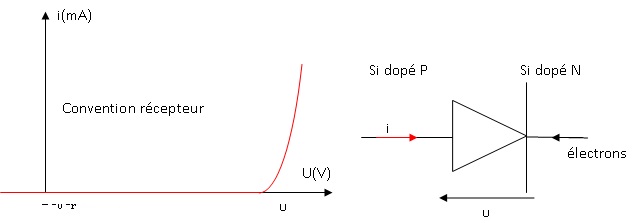
24. La diode à
jonction est constituée d'une jonction PN. Représenter le symbole
normalisé d'une diode, faire le lien entre ce schéma et les zones P et
N de la jonction. Tracer l'allure de la carctéristique courant-tension
d'une diode à jonction, en précisant les conventions d'orientations
choisies sur le symbole normalisé.
|
|
|