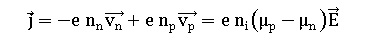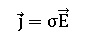Propriétés
électriques des semi-conducteurs.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Dans
un semi-conducteur pur, à très basse température ( 0 K), on tend vers
la structure idéale où tous les électrons de valence sont engagés dans
des liaisons covalentes..A une température T, l'agitation thermique
rompt quelques liaisons covalentes. Un électron de charge -e, faisant
habituellement partie d'une liaison covalente est délogé et devient
alors libre laissant une liaison covalente incomplète appelé trou
auquel on associe une charge +e. Les trous comme mes électrons
contribuent à la conduction électrique.
On note n la concentration en électrons et p la concentration en trous.
Pour un semi-conducteur pur, appelé aussi semi-conducteur intrinsèque,
les concentrations en trous et en électrons sont égales, soit n = p = ni,
où ni est appelée concentration intrinsèque.
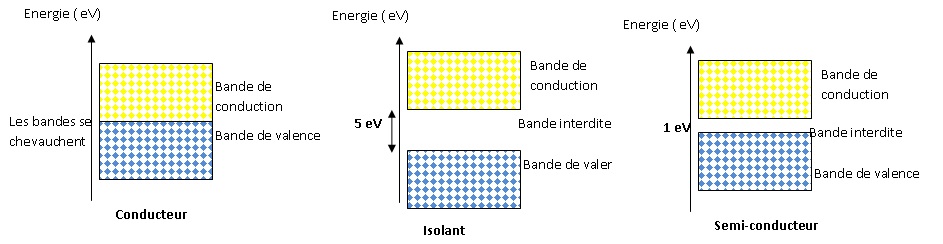
1.
Représenter, sur un diagramme énergétique, les niveaux d'énergie que
peuvent occuper les électrons dans un conducteur, dans un
semi-conducteur puis dans un isolant.
2.
Pour le silicium, à 300 K, comparer la concentration intrinsèque aux
nombre d'atomes de silicium par unité de volume et commenter.
Nombre d'atomes de silicium à 300 K : nSi = 5 1028
m-3.
ni = 1,5 1016 m-3. Ce nombre est très
faible comparé au nombre d'atomes, le silicium est donc un
semi-conducteur.
Sous l'action d'un champ électrique E, les électrons et les trous se
mettent en mouvement. La vitesse d'ensemble d'un type de porteurs est
liée au champ électrique par la relation 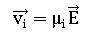 où µi est lamobilité du porteur. où µi est lamobilité du porteur.
3. Qu'appelle t-on
vitesse d'ensemble d'un type de porteur ? Quelle est l'unité de µi
dans le système internationnal ?
On notera µn et µp les mobilités respectives des
électrons libres et des trous.
µn = -1500 10-4 SI ; µp =475
10-4 SI.
Donner une interprétation qualitative de la différence d'ordre de
grandeur entre ces deux valeurs.
La vitesse d'ensemble d'un type de porteur de charge est la vitesse
moyenne de ces porteurs.
La vitesse s'exprime en m s-1 et le champ électrique en V m-1.
µ s'exprime en m2 V-1 s-1.
Pour déplacer un trou, il faut que plusieurs électrons se déplacent
successivement ; la mobilité d'un trou est donc inférieure à celle d'un
électron.
On associe au mouvement d'ensemble des charges le vecteur densité de
courant.
4. Donner
l'expression du vecteur densité de courant en fonction de ni,
e et des vitesses d'ensemble des charges puis en fonction de ni,
e, µn, µp et du champ électrique. Donner la
dimension de ce vecteur et son unité.
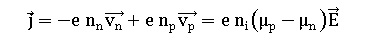
Le vecteur densité de courant s'exprime en A m-2.
5. Après avoir
énoncé la loi d'Ohm locale, exprimer la conductivité électrique s du semi-conducteur pur en
fonction de ni, e, µn et µp. Quelle
est l'unité de s
dans le système internationnal ? Donner la valeur numérique de s pour le silicium à 300 K.
Loi d'Ohm locale : 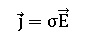
On identifie : s
= e ni(µp-µn).
j s'exprime en A m-2 et E en V m-1 : s s'exprime en A m-1
V-1.
sSi
= 1,602 10-19 x 1,5 1016(475-(-1500))10-4
=4,7 10-4 A
m-1 V-1.
6. Expliquer
qualitativement comment varie la concentration intrinsèque ni,
puis la conductivité électrique dans un semi-conducteur avec la
température.
Le nombre de paire électron-trou augmente avec la température. Le
nombre de porteurs de charge et la conductivité croît avec la
température.
|
...
|
|
.
|
....
|
7.
A partir de la loi d'Ohm locale, établir la loi d'Ohm intégrale pour un
barreau cylindrique de section droite S et de longueur L parcouru par
un courant axial permanent réparti uniformément. En déduire sa
résistance R en fonction de s,
L et S. Calculer R si L = 1 cm et de rayon r = 1 mm à 300 K.
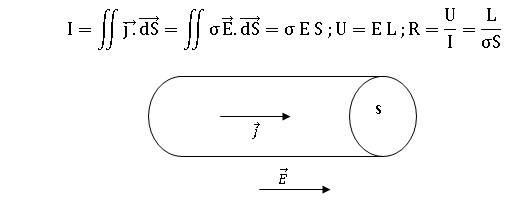
S = p r2
= 3,14 x 10-6 m2 ; R = 10-2 / (4,7 10-4
x3,14 10-6) = 6,8 106 ohms.
8.
Dans le cas d'un métal comment varie la résistance R avec la
température ? Justifier qualitativement. Calculer R pour un barreau de
cuivre de mêmes dimensions que le barreau décrit à la question 7. s Cu = 59,6 106
SI.
Le
nombre de porteurs de charges ( électrons libres du métal) ne dépend
pas de la température. Plus la température est élevée, plus le réseau
cristallin vibre, se désorganise, et en conséquence la conductivité du
métal diminue.
R = 10-2
/ (59,6 106 x3,14 10-6) =5,3 10-5 ohms.
9. Lors de l'étude
d'une thermistance réalisée avec des poudres semi-conductrices
agglomérées, un professeur de terminale S a fait mesurer à ses élèves
la résistance du dipôle à différentes températures.
A trois températures différentes, les valeurs suivantes de la tension
aux bornes du dipôle et de l'intensité du courant qui le traverse en
convention récepteur ont été collectées par les différents groupes.
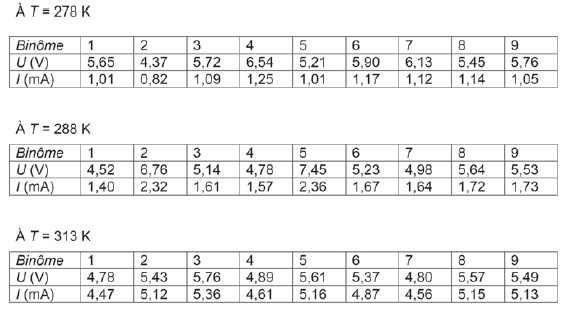
Déterminer pour la température T = 278 K, la valeur moyenne de la
résistance ainsi qu'une estimation de l'incertitude sur cette valeur.
Proposer une exploitation pédagogique de l'ensemble des données
collectées par les élèves.
Rmoyen = (5,65 / 1,01 + 4,37 / 0,82 + 5,72 / 1,09 +6,54 /
1,25 +5,21 / 1,01 +5,90 / 1,17 +6,13 / 1,12 +5,45 /1,14 +5,76 /1,05) /
9 ~5,3 ohms.
Ecart type s
= 0,08 ohm.
R = Rmoyen ± 2 s pour un intervalle de
confiance de 95 %.
R = 5,3 ±0,2 ohms.
Exploitation
pédagogique : thème structure et propriétés des matériaux.
Problèmatique
: les résultats des mesures permettent-elles de conclure sur
l'évolution de la résistance d'une thermistance avec la température.
Les élèves doivent calculer la résistance moyenne et l'incertitude sur
les trois séries de mesures. Ils doivent ensuite conclure à la
problématique.
|
|

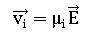 où µi est lamobilité du porteur.
où µi est lamobilité du porteur.