D’après le Capitaine Nemo : « C’est
un cylindre très allongé, à bouts coniques.
Il affecte sensiblement la forme d’un cigare, [. . . ] ». Même si
certaines caractéristiques du submersible semblent aujourd’hui encore
irréalistes, d’autres sont étonnamment proches de celles de sous-marins
modernes.
Des élèves ont réalisé des expériences, dans le cadre des Olympiades de
la Physique, pour comprendre l’intérêt de la forme en cigare du
Nautilus.
Q 24 Établir
l’équation différentielle vérifiée par la vitesse v d’un objet lors de
sa chute dans un fluide. Les frottements fluides exercés sur l’objet
sont modélisés par une force 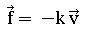 , k étant une constante positive et v la vitesse du système étudié par
rapport au milieu considéré au repos dans le référentiel d’étude.
, k étant une constante positive et v la vitesse du système étudié par
rapport au milieu considéré au repos dans le référentiel d’étude.
r
= 900 kg m-3 masse volumique du fluide ; V : volume de
l'objet.
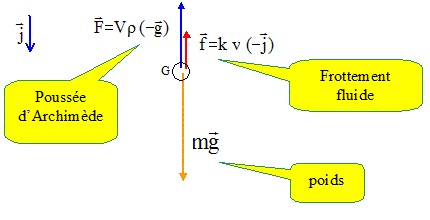
Ecrire la
seconde loi de Newton en projection sur l'axe vertical orienté vers le
bas.
mg -k v -r V g = m dv /dt.
dv /dt +k / m v = g(1-r
V / m). (E)
Q 25 Donner
l’expression littérale de la vitesse v (t) de l’objet, solution de
l’équation différentielle trouvée à la question précédente. En déduire
l’expression de k en fonction de la vitesse limite et d’autres
paramètres du problème.
Solution générale de dv /dt + k / m v = 0 : v(t) = A exp(-k/m t) avec A
une constante.
Solution particulière de (E) : vlimite = g / k(m-r V ).
Solution générale de (E) : v(t) = A exp(-k / m t) + vlimite.
A est déterminée par la condition initiale v(t=0) = 0 ; A = -vlimite.
v(t) = vlimite
( 1-exp(-k/m t).
k = g(m-rV)
/vlimite
.
Q 26 Les élèves ont
tracé les tangentes à la courbe à l’origine et à l’infini : quelles
informations peut-on en tirer ?
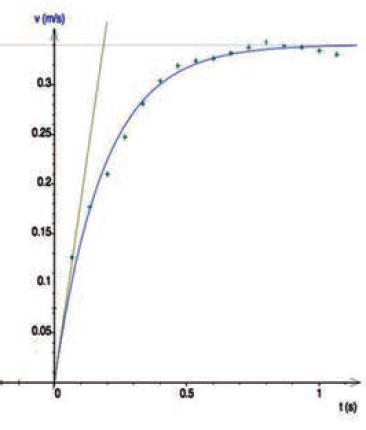
La
tangente à la courbe à l'infini donne la vitesse limite vlimite
= 0,34 m /s.
La tangente à l'origine donne la constante de temps m / k = 0,2 s.
Q 27 Déduire des
résultats expérimentaux la valeur de k pour chaque objet. Conclure.
vlimite (cube) = 0,2587 m /s ; vlimite (sphère) =
0,268 m /s ; vlimite (Nautilus) = 0,3404 m /s.
Les objets ont la même masse m = 7,0 g et le même volume V =4 cm3.
kcube = 9,8(4 10-3
-4 10-6 x900) /0,2587 =3,92 10-3/
0,2587 ~ 1,5 10-2 kg / s ;
ksphère = 3,92 10-3 / 0,268 ~1,46 10-2
kg / s.
kNautilus = 3,92 10-3 / 0,3404 ~1,15 10-2
kg/ s.
La forme en cigare du Nautilus améliore son hydrodynamisme.
Q 28 Sachant que
pour l’eau de mer r
= 1026 kg·m−3 et h
= 1,07.10−3 Pa·s à 20 °C, expliquer le choix de l’huile pour
réaliser l’expérience. Viscosité de l'huile 60 10-3 Pa
s.
L'huile et l'eau de mer ont des masses volumiques voisines. Par contre,
l'huile possède une viscosité 60 fois plus grande que celle de l'eau de
mer. Dans le cas de l'huile, la vitesse limite serat faible. Le
pointage vidéo en sera bien plus commode.
Q 29
En considérant les valeurs des vitesses limites données par les élèves,
formuler quelques conseils pour écrire convenablement le résultat d’une
mesure.
Evaluer les sources d'incertitudes et en déduire celle du résultat.
Connaissant cette incertitude, on ne garde pas trop de nombre de
chiffres significatifs ; le résultat ne doit pas être plus précis
que l'incertitude.
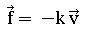 , k étant une constante positive et v la vitesse du système étudié par
rapport au milieu considéré au repos dans le référentiel d’étude.
, k étant une constante positive et v la vitesse du système étudié par
rapport au milieu considéré au repos dans le référentiel d’étude.
